Лабораторная работа №4.Решение разностных уравнений.

Обыкновенное разностное уравнение порядка n есть уравнение

G (x _k , y _k, y _k+1 ,….y _{k +n})=0 , (1)

(k=0,1,2,….),

связывающее значения y _k = y (х _k) = у (x₀ + k Δx) функции у = у(х) на дискрет­ном множестве значений x = x _k = x ₀ +k Δx, где Δx — фиксированное прираще­ние. Часто бывает удобно ввести в качестве новой независимой переменной величину

k =(x-x₀ )/ Δx = 0, ± 1, ±2,;...

Решением разностного уравнения называется такая функция у =у (х ), что последовательность у_k удовлетворяет данным уравнениям для некоторой области значений k. Общее решение обыкновенного разностного уравнения порядка n содержит, вообще говоря, n произвольных постоянных, которые должны быть определены по начальным, краевым или другим дополнительным условиям, налагаемым на у_k. Решение разностного уравнения в любой конеч­ной области значений k сводится в принципе к решению системы алгебраических уравнений.

Разностные уравнения применяются:

I) для аппроксимации дифференциальных уравнений,

2) для решения задач, представляющих модели с дискретными переменными.

Разностное уравнение порядка “n”

, (2)

в котором все коэффициенты – константы, называется линейным разностным уравнением с постоянными коэффициентами. Если правая часть f(k)=0, уравнение называется однородным.

Общее решение такого однородного уравнения имеет вид:

(3)

где - корни характеристического уравнения

(4)

Для частного решения разностного уравнения порядка n должно быть задано n начальных или краевых условий по которым определяются константы С в уравнении (3).

Пример решения разностного уравнения второго порядка.

Задано уравнение

. (5)

Заданы начальные условия: . Его характеристическое уравнение:

(6)

Отсюда . (7)

И решение равно:

. (8)

Значения констант определяем из начальных условий:

(9)

Подставив в (9) значения начальных условий и вычисленные в (7) значения корней характеристического уравнения, и решив систему из двух линейных алгебраических уравнений , получим значения констант С.

Задача 1. Задано разностное уравнение второго порядка

с начальными условиями

Пользуясь калькулятором, решить его и вычислить первые пять значений y.

В случае уравнений порядка выше второго характеристическое уравнение, константы значения самой функции у можно вычислять на ЭВМ, в частности, в пакете Маткад.

З адача 2. Решить в маткаде разностное уравнение третьего порядка и построить график решения:

.

Заданы начальные условия:

1. Характеристическое уравнение имеет вид: .

Решаем его в Маткаде с помощью функции polyroots:

Корни получены в виде матрицы, причем ее первый элемент

второй третий-

Решение разностного уравнения ищем по формуле .

2. Отсюда находим соотношения для констант С₀, С₁, С₂:

С₀+С₁+С₂=1

С₀z₀+C₁z₁+C₂z₂=0

C₀z₀²+C₁z₁²+C₂z₂²=0.

Решая эту систему в Маткаде, определяем значения констант.

Здесь до слова Given заданы начальные приближения неизвестных. Сначала все они были заданы равными 1. Однако Пакет попросил изменить их. Поэтому для С2 было принято начальное значение 10.

Строим график, выбирая в окне настройки не «линии»(lines), а «точки» (points).

Задача 2.. Решить самостоятельно в маткаде нижеприведенные разностные уравнения. Построить графики их решения для 20 точек.

А). Начальные условия:

Б). Начальные условия:

ЛАБОРАТОРНАЯ РАБОТА №5.РЕГРЕССИИ.

В Маткаде имеется большое количество встроенных функций по обработке наблюдений:

Линейная регрессия

1.Функция slope (vx, vy) – возвращает коэффициент «a» линейной регрессии y=ax+b векторов vx и vy.

2. Функция intercept ( vx, vy) – возвращает коэффициент «b» линейной регрессии векторов vx и vy.

Эти обе функции используются для линейной регрессии.

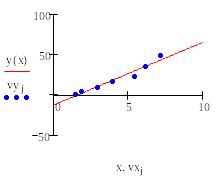
На рис. 1 показано вычисление коэффициентов линейной регрессии с помощью этих функций. Как известно, линейная регрессия вычисляется по результатам измерений входного и выходного сигналов системы. Здесь vx- вектор входных сигналов, vy- вектор выходных сигналов. По ним функциями slope и intercept мы находим коэффициенты прямой линии, наилучшим образом сглаживающей ошибки измерения. Затем записываем уравнение этой прямой и строим для нее график.

Рис.1. Вычисление линейной регрессии.

Задача 1. Решите в маткаде приведенный выше пример.

Задача 2. Вычислите коэффициенты линейной регрессии и постройте график для измерений:

х	1.78	2.86	3.32	5.90	6.27	7.10	7.99
y	56.7	53.9	48.0	41.2	39.6	36.3	37.1

Нелинейная регрессия.