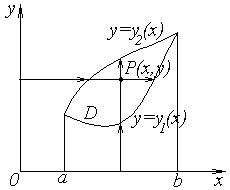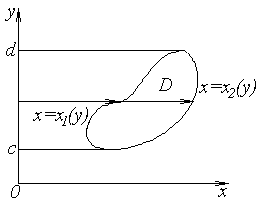20

1 Двойные и тройные интегралы

1. Двойной интеграл

1. Двойной интеграл и его приложения

Пусть ограниченная функция определена в некоторой замкнутой области плоскости Разобьем область произвольным образом на меньших областей не имеющих общих внутренних точек, в каждой части возьмем произвольную точку , вычислим значение и составим сумму

(1.1)

где ― площадь

Эта сумма называется интегральной суммой функции , соответствующей данному разбиению области на части и данному выбору промежуточных точек .

Диаметром ограниченного множества назовем точную верхнюю грань расстояний между двумя произвольными точками этого множества:

Пусть ― диаметр , .

Если существует предел интегральной суммы (1.1) при не зависящий от способа дробления области на части и выбора точек в них, то он называется двойным интегралом от функции по области и обозначается

т. е.

а функция называется интегрируемой в области .

Если функция непрерывна в замкнутой области , то она интегрируема в этой области.

Двойные интегралы обладают такими же свойствами, как и определенные интегралы (линейность, аддитивность, формулы среднего значения и т. д.).

Геометрический смысл двойного интеграла: если в области то двойной интеграл

(1.2)

численно равен объему цилиндрического тела с основанием и образующей, параллельной оси которое ограничено сверху поверхностью (рисунок 1.1).

Рисунок 1.1

В частности, когда двойной интеграл (1.2) равен площади области т. е.

. (1.3)

Физический смысл двойного интеграла: если область ― плоская пластинка, лежащая в плоскости с поверхностной плотностью распределения вещества, то массу пластинки находят по формуле

(1.4)

статические моменты пластинки относительно осей и находят по формулам:

(1.5)

координаты центра масс пластинки:

(1.6)

моменты инерции пластинки относительно осей координат и начала координат:

(1.7)

Область которая определяется неравенствами где и ― однозначные непрерывные функции на отрезке называется стандартной относительно оси Аналогично определяется стандартная область относительно оси

Область стандартную как относительно оси так и относительно оси называют просто стандартной областью. На рисунке 1.2 показана стандартная относительно оси область

В случае стандартной области всякая прямая, параллельная оси координат и проходящая через внутреннюю точку области пересекает границу области в двух точках (рисунок 1.2).

Рисунок 1.2 Рисунок 1.3

Если ― область интегрирования, стандартная относительно оси двойной интеграл вычисляется по формуле

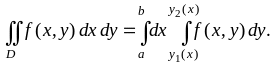(1.8)

Правую часть формулы (1.8) называют повторным интегралом, а интеграл

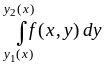
называют внутренним интегралом.

Вычисление повторного интеграла следует начинать с вычисления внутреннего, в котором переменную надо принять при интегрировании за постоянную величину. Результат интегрирования будет некоторой функцией от которая интегрируется затем по отрезку В результате получается некоторое число ― значение интеграла (1.8).

Если область является стандартной относительно оси (рисунок 1.3), двойной интеграл вычисляется по формуле

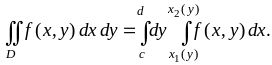(1.9)

Процесс расстановки пределов интегрирования для внутреннего и внешнего интегралов называется приведением двойного интеграла к повторному, а переход от формулы (1.8) к формуле (1.9) или наоборот ― изменением порядка интегрирования.

Если область не является стандартной ни относительно оси , ни относительно оси , ее разбивают на конечное число областей стандартных относительно оси (или ), и при вычислении двойного интеграла по области используют свойство аддитивности.