Тема: Методы сортировки и применение встроенных датчиков псевдослучайных чисел.

Теоретическая и практическая часть

1. Методы сортировки

Упорядочение элементов множества в возрастающем или убывающем порядке называется сортировкой.

С упорядоченными элементами проще работать, чем с произвольно расположенными: легче найти необходимые элементы, исключить, вставить новые. Сортировка применяется при трансляции программ, при организации наборов данных на внешний носителях, при создании библиотек, каталогов, баз данным и т. д.

Алгоритмы сортировки можно разбить на следующие группы: (рис. 1).

Методы сортировки

Сортировка в линейных структурах

С ортировка в нелинейных структурах

вставка		выбор		обмен		турнирная		п ирамидальная
простая вставка		простой выбор		стандартный обмен
				Метод Шелла
бинарная вставка				Метод Хоара

Рис. 1 Алгоритмы сортировки

Обычно сортируемые элементы множества называют записями и обозначают через .

1.1. Сортировка выбором

Сортировка выбором состоит в том, что сначала в неупорядоченном списке выбирается и отделяется от остальных наименьший элемент. После этого исходный список оказывается измененным. Измененный список принимается за исходный и процесс продолжается до тех пор, пока все элементы не будут выбраны. Очевидно, что выбранные элементы образуют упоря­доченный список.

Например, требуется найти минимальный элемент списка:

{5, 11,6,4,9,2, 15, 7}.

Процесс выбора показан на рис. 2, где в каждой строчке выписаны сравниваемые пары. Выбираемые элементы с меньшим весом подчеркнуты. Нетрудно видеть, что число сравнений соответствует на рисунке числу строк, а число перемещений — количеству изменений выбранного элемента.

{5, 11, 6, 4, 9, 2, 15, 7}

5 11

5 6

5 4

4 9

4 2

2 15

2 7

2

Рис. 2. Сортировка выбором

Выбранный в исходном списке минимальный элемент размещается на предназначенном ему месте несколькими способами:

• минимальный элемент после i-го просмотра перемещается на i-е место нового списка (i =1, 2, ..., п), а в исходном списке на место выбранного элемента записывается какое-то очень большое число, превосходящее по величине любой элемент списка, при этом длина заданного списка остается постоянной. Измененный таким образом список можно принимать за исходный;

• минимальный элемент записывается на i-е место исходного списка ( 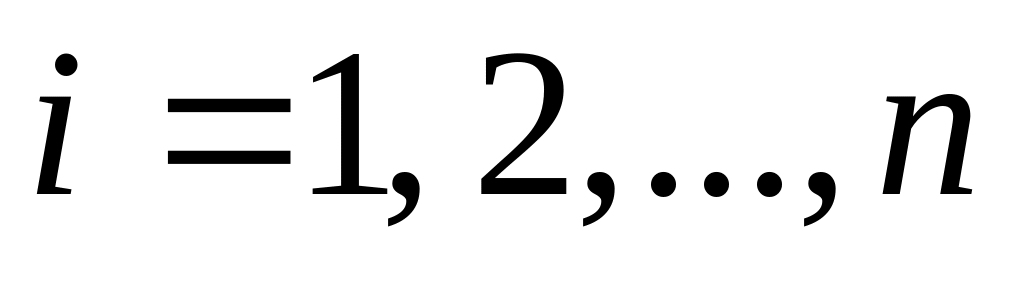), а элемент с i-го места — на место выбранного. При этом очевидно, что уже упорядоченные элементы (а они будут расположены, начиная с первого места) исключаются из дальнейшей сортировки, поэтому длина каждого последующего списка (списка, участвующего в каждом последующем просмотре) должна быть на один элемент меньше предыдущего;

• выбранный минимальный элемент, как и в предыдущем случае, перемещается на i-е место заданного списка, а чтобы это i-е место освободилось для записи очередного минимального элемента, левая от выбранного элемента часть списка перемещается вправо на одну позицию так, чтобы заполнилось место, занимаемое до этого выбранным элементом (элементы списка циклически сдвигаются).

Сложность метода сортировки выбором порядка составляет О(п²).