Стоячие и бегущие волны

Рассмотрим одно из частных решений волнового уравнения:

(9)

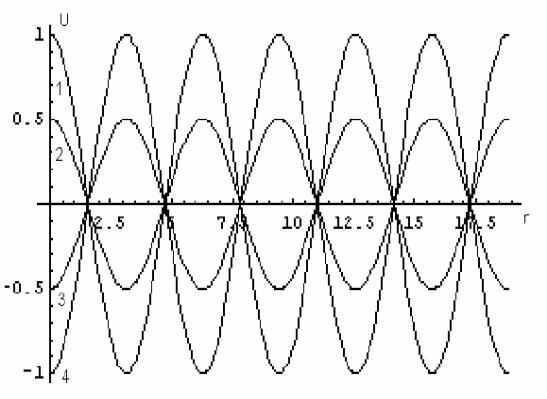
Построим график зависимости функции U от безразмерной координаты r = kx для нескольких различных моментов времени. График представлен на рис.

В начальный момент t = 0 волновое поле изображено кривой 1. Кривая 2 показывает состояние поля через 1/6 временного периода ( ). Спустя 1/3 периода после начального момента волна принимает состояние 3. Наконец, через половину периода поле придет к графику кривой 4. Далее все пойдет в обратном порядке – от 4 к 3, от 3 к 2 и так далее. Как можно видеть из рисунка, положения точек экстремумов (пучностей) и точек нулей (узлов) функции во времени не изменяются. В этой связи данное решение называют стоячей волной. Функция, изображающая изменения волны в пространстве, периодична. Поскольку периодом синуса или косинуса является число 2π, пространственный период волны, как это следует из (9), равен λ = 2π/k. Число λ называют длиной волны. Совершенно по иному изменяется во времени и пространстве решение вида:

. (10)

На рис. представлены «мгновенные снимки» графиков функции (10) в несколько последовательных моментов времени.

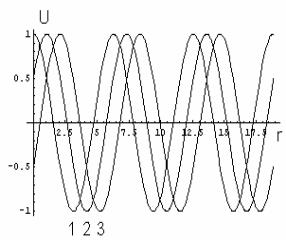
Здесь, аналогично предыдущему рисунку, показаны графики функции U в зависимости от безразмерной переменной r. Кривыми 1, 2 и 3 представлены состояния волнового поля в момент времени t = 0, спустя 1/3 временного периода и спустя 2/3 временного периода, соответственно. В отличие от стоячей волны, в данном решении точки нулей, точки экстремумов, как и вся кривая в целом, перемещаются в пространстве. При положительном значении волнового числа смещение синусоиды происходит слева направо, при отрицательном – справа налево. Положение любой фиксированной фазы волны ωt-kx=const смещается с течением времени. Вследствие этого, решение, задаваемое формулой (10), называют бегущей волной. Нетрудно видеть, что в бегущей волне точка любой фиксированной фазы движется с постоянной скоростью , которая называется фазовой скоростью. Типичным примером стоячей волны являются колебания в натянутой и закрепленной на концах струне. Поскольку концы зафиксированы, они должны соответствовать узлам синусоид. Тогда на длине струны L должно укладываться целое число половин длин волн, то есть L =nλ/2, n = 1, 2, 3, … . Мода, у которой на длине струны укладывается только одна половина длины волны, называется основной. Это – самая низкочастотная стоячая волна. Ее частота равна . Примерами бегущей волны являются волны на поверхности воды, звуковые волны в неограниченном пространстве.

Плоские, сферические и цилиндрические волны

До сих пор мы рассматривали решения волнового уравнения в одномерном случае. Для изучения волн в пространстве трех измерений обратимся к обобщению волнового уравнения:

. (11)

Оператор Лапласа в прямоугольной декартовой системе координат имеет вид

и волновое уравнение в декартовой системе координат будет иметь вид

. (12)

Точка А в декартовой системе координат определяется тремя координатами x,y,z или радиус вектором r(x,y,z).

Решение, удовлетворяющее уравнению (12) и соответствующее понятию бегущей волны с единичной амплитудой, может быть представлено в виде:

, (13)

- волновой вектор. Модуль волнового вектора , как и в одномерном случае, определяется длиной волны. Для того, чтобы выяснить, что определяет направление волнового вектора, необходимо ввести новые понятия волновой физики. Определим, что представляет собой поверхность в трехмерном пространстве, на которой фаза волны в данный момент постоянна. Для этого зафиксируем значение фазы в аргументе косинуса в (13):

(14)

Из аналитической геометрии известно, что соотношение (14) задает плоскость в трехмерном пространстве. Поверхность, на которой в данный момент времени волна имеет одну и ту же фазу, называют фазовым фронтом, или фазовой поверхностью. Единичный вектор, ортогональный фазовому фронту и направленный во внешнюю относительно начала системы координат сторону, называется фазовой нормалью. Итак, волновым вектором является такой вектор, длина которого численно равна волновому числу 2π/λ, а направление совпадает с направлением фазовой нормали. Волна, у которой фазовый фронт представляет собой плоскость, называется плоской волной. Очевидно, что фазовый фронт в бегущей волне перемещается в пространстве с течением времени. Именно это перемещение и следует рассматривать как распространение волн. Очевидно также, что перемещение фазового фронта в пространстве происходит с фазовой скоростью.

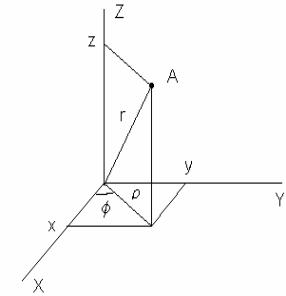
В сферической системе координат положение точки А определяется радиусом ρ, и двумя углами φ и θ, как это показано на рис.

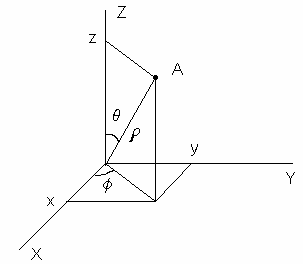
Оператор в данном случае представляется в виде:

. (15)

Ограничимся рассмотрением поля с центральной симметрией. При этом зависимостей от углов (полярного θ и азимутального φ) не будет. Частные производные по углам в (15) равны нулю. Использовав только первые два слагаемых в (15), из (11) получим:

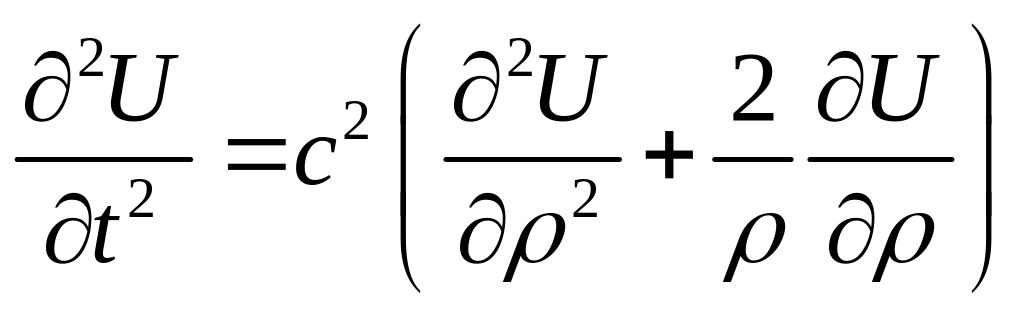(16)

Будем, как обычно, искать гармоническое во времени решение . При этом на пространственную часть решения получим обыкновенное дифференциальное уравнение:

. (17)

Подстановкой удается привести (17) к стандартному виду:

. (18)

Решение последнего уравнения нам известно. Представив его в комплексной форме и перейдя к исходной функции U, мы будем иметь:

. (19)

Вещественная часть от полученной формулы дает решение волнового уравнения в виде расходящейся (при знаке «-» в предыдущей формуле) сферической волны:

. (20)

Сферичность волны связана с тем, что фазовый фронт kρ = const здесь представляет собой сферическую поверхность с центром в начале координат. Важнейшей особенностью сферической волны является то, что ее амплитуда зависит от координат, а именно, обратно пропорциональна расстоянию до начала системы. Следует отметить, что решение (20) имеет особенность в точке ρ = 0, а, следовательно, неправомерно в начале координат. Представление решения волнового уравнения в виде сферической волны удобно использовать, когда источник волн можно считать точечным, то есть, когда расстояние от точки наблюдения до источника много больше линейного размера источника. Непосредственно форма (20) применима к изотропному источнику, равномерно излучающему волны во все направления, однако, модель сферической волны можно применить и к анизотропному источнику. Примером анизотропного источника может служить линейная антенна (электрический диполь), излучающая радиоволны. Для учета анизотропии источника формулу (20) достаточно дополнить множителем, описывающим угловое распределение интенсивности излучения:

. (21)

Функция Ф(φ, θ) является угловой диаграммой направленности излучателя.

В цилиндрической системе координатами, определяющими положение точки в пространстве являются азимутальный угол φ, радиус ρ и координата z. Волновое уравнение здесь будет выглядеть следующим образом:

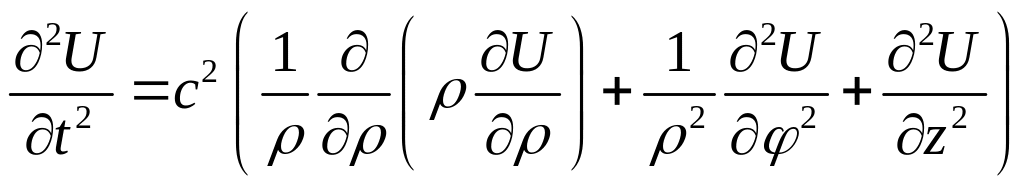. (22)

Рассмотрим поле с осевой симметрией и не зависящее от z. При этом в правой части (22) остается только первое слагаемое. Кроме того, как обычно, полагаем зависимость от времени гармонической. Тогда для функции от радиуса будем иметь уравнение:

. (23)

Данное уравнение является уравнением Бесселя. В простейшем случае его решением является функция Бесселя первого рода, нулевого порядка . Поведение функции Бесселя в зависимости от безразмерного аргумента х показано на рис.

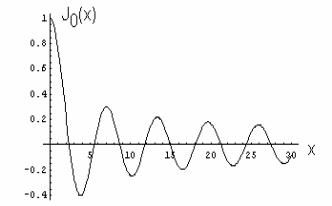
Как можно видеть из графика, при больших значениях аргумента функция ведет себя подобно тригонометрическим функциям синуса или косинуса с убывающей с ростом аргумента амплитудой. На самом деле решение уравнения типа (23) может быть представлено и функцией Бесселя второго рода . Полное решение с учетом временной зависимости можно записать в виде:

. (24)

С равным успехом можно было бы использовать во временной зависимости функцию синуса или любые комбинации синуса и косинуса. Очевидно, фазовая поверхность ρ = const представляет собой цилиндрическую поверхность. Естественно, что такая волна называется цилиндрической. В противоположность точечному источнику, порождающему сферические волны, цилиндрические волны описывают волновое поле на расстояниях от линейного источника, много меньших его длины. Аналогично тому, как это делалось для сферических волн, можно ввести диаграмму направленности и для источника цилиндрических волн Ф(φ) – зависимость интенсивности излучения от азимутального угла.

Плоские и сферические волны, описанные здесь, соответствуют бегущим волнам, в то время как цилиндрическая волна в форме (24) является стоячей. Скомпоновать плоские и сферические стоячие волны не представляет труда. Необходимо только разделить временные и пространственные части и представить их в виде соответствующих тригонометрических функций. Несколько сложнее обстоит дело с представлением бегущей цилиндрической волны. Необходимо исходить из того, что функции Бесселя первого и второго рода имеют асимптотики при больших значениях аргумента в виде косинуса и синуса, соответственно, и с амплитудой, обратно пропорциональной аргументу. Тогда, в соответствии с тригонометрическим тождеством , бегущая цилиндрическая волна должна быть записана в виде:

. (25)

На оси цилиндра такое решение имеет особенность (обращается в бесконечность).

Плоские, сферические и цилиндрические волны являются модельными описаниями волновых полей. Для конкретных задач та или иная модель становится предпочтительной. В то же время любое «достаточно хорошее» волновое поле может быть описано любой из этих моделей. Дело в том, что и тригонометрические функции, используемые в плоских и сферических волнах, и бесселевы функции в цилиндрических волнах являются ортогональными. Следовательно, любую, опять же «достаточно хорошую», функцию можно разложить в интеграл Фурье или интеграл Фурье–Бесселя.