Электромагнитные волны в вакууме

В среде, в отсутствие зарядов и токов уравнения Максвелла выглядят следующим образом (система СГС):

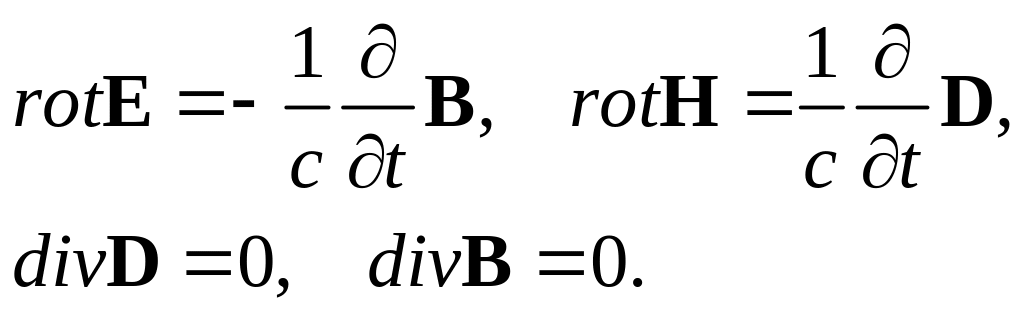
В уравнениях Максвелла вектор E, характеризующий воздействие поля на заряд, есть вектор напряженности электрического поля. Вектор B, характеризующий воздействие поля на элемент тока называется вектором магнитной индукции. Вектор электрической индукции D – результирующее электрическое поле в среде, индуцированное наложенным полем E. В то же время, в силу исторических причин, наоборот, вектор напряженности магнитного поля H есть результирующее магнитное поле в среде, наведенное внешним полем B. с – скорость света в вакууме.

Связи между рассматриваемыми векторами задаются так называемыми материальными уравнениями, которые в вакууме имеют форму:

, т.к. магнитная и диэлектрическая проницаемости вакуума равны единице

то уравнения максвелла принимают вид

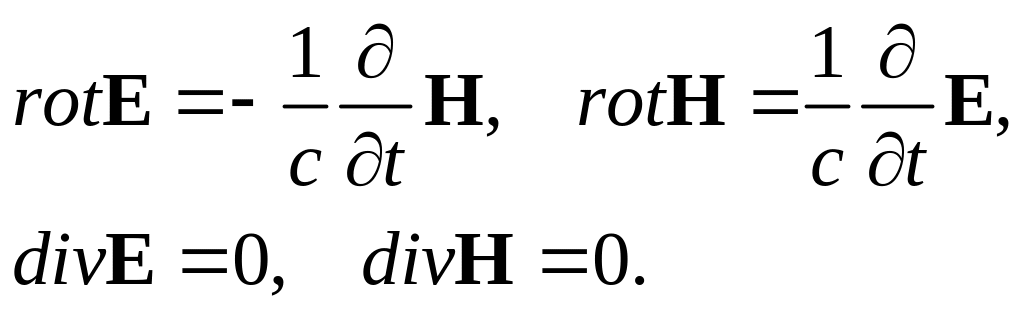
Действуя оператором rot на первое уравнение, и подставляя в полученное, второе уравнение получим

Из векторного анализа известно, что , а т.к. , то мы получаем волновое уравнение для вектора

.

- оператор Лапласа.

Аналогично можно получить уравнение для .

Решения волнового уравнения Решение одномерного волнового уравнения

Выше мы показали, что разнообразные физические модели сводятся к их описанию с помощью однотипного волнового уравнения, которое в одномерном случае еще раз запишем таким образом:

(1)

Прежде всего, покажем, что любая функция , зависящая от координаты и времени, объединенных в линейную комбинацию, удовлетворяет волновому уравнению. Рассмотрим это для комбинации . В соответствии с правилом дифференцирования сложной функции, получим

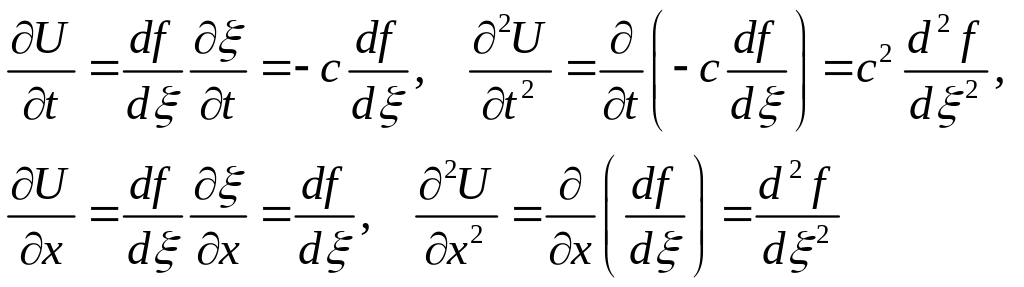
сравнивая вторые производные от U по t и x, видим что они отличаются только множителем с², так что функция от линейной комбинации будет решением волнового уравнения.

Положение точки заданного значения аргумента в пространстве перемещается со скоростью с. При этом, если в указанной линейной комбинации выбран знак «-», то точка движется в положительном направлении оси х. При знаке «+» движение происходит в противоположную сторону. Из этого следует, что одним из частных решений волнового уравнения будет произвольный профиль U(x), перемещающийся вправо или влево с постоянной скоростью с без изменения формы (рис.).

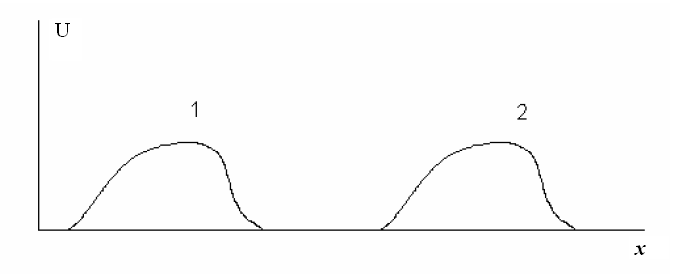
На рис. представлен «мгновенный снимок» решения в два момента времени. В начальный момент профиль занимает положение 1, спустя некоторое время – положение 2. Форма кривой не претерпевает изменений. При замене знака «-» на «+» следует, наоборот, считать, что начальное положение есть 2, а конечное – 1.

Волновым решением уравнения (1) будем называть решение, гармоническое, как во времени, так и в пространстве. Покажем один из возможных способов получения волнового решения. Будем искать его методом разделения переменных, то есть попытаемся отыскать решение в форме:

U(x,t) = X(x)T(t). (2)

Здесь X(x) – функция только координаты, а T(t) – функция только времени.

Подставив (2) в (1) и разделив левую и правую части на произведение XT, мы получим:

. (3)

Поскольку Т и Х зависят только от своих единственных аргументов, далее более правильно использовать не частные производные, а обыкновенные.

В левой части (3) может быть зависимость только от t, а в правой – только от х. Такое возможно, только если и левая и правая части не зависят ни от времени, ни от координаты. Следовательно, обе части равны одной и той же постоянной, которую мы обозначим как p². Теперь из уравнения (3) мы получаем два обыкновенных дифференциальных уравнения:

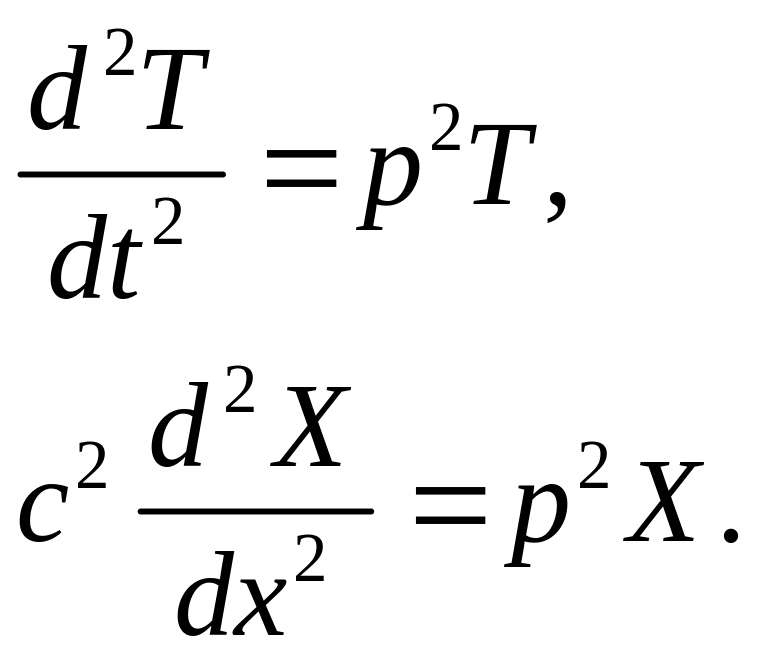(4)

Будем искать решение первого из этих уравнений в виде . Подстановка в соответствующее уравнение приводит к так называемому характеристическому уравнению , имеющему два корня +p и –p. Общее решение записывается в форме

(5)

А₁ и А₂ – произвольные комплексные постоянные. Поскольку нас интересует волновое (периодическое во времени) решение, необходимо считать константу p чисто мнимой величиной p = iω. В этом случае , и комбинируя комплексные постоянные А₁ и А₂, можно получить любое из колебательных решений. Очевидно, что величина ω имеет тот же смысл, что и при рассмотрении колебательных процессов – циклическая частота. Подстановка p = iω во второе из уравнений (4) приводит к соотношению, формально совпадающему с уравнением колебаний, в котором время t заменено координатой х:

(6)

Отношение , имеющее размерность обратной длины, называется волновым числом. Частными решениями (6) будут функции , cos(kx), sin(kx), которые можно комбинировать в виде сомножителей с (5). Стандартным волновым решением (или просто волной) в одномерном случае будем называть решение

, (7)

или его комплексный аналог

. (8)

Преобразованием начальной фазы можно перейти от к . Кроме того, произведения , , , также будут удовлетворять исходному волновому уравнению.