Отражение и преломление объемных поперечных электромагнитных волн на границе раздела сред

Рассмотрим падение поперечной электромагнитной волны (рис.) из прозрачной среды на плоскую границу раздела прозрачной среды (эту среду будем обозначать индексом I) с любой другой средой (которую обозначим индексом II). Падающую волну обозначим индексом 0, отраженную – индексом 1, преломленную – индексом 2. Угол падения волны на границу, отсчитываемый от нормали к границе, обозначим _о, угол отражения ₁, угол преломления – ₂.

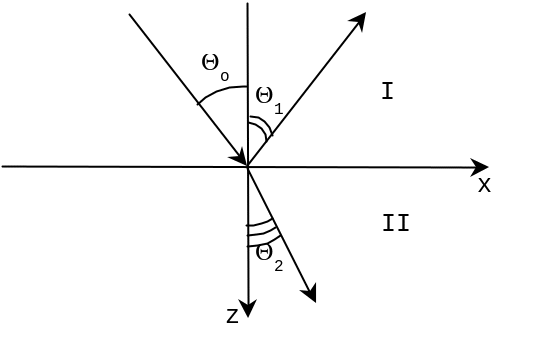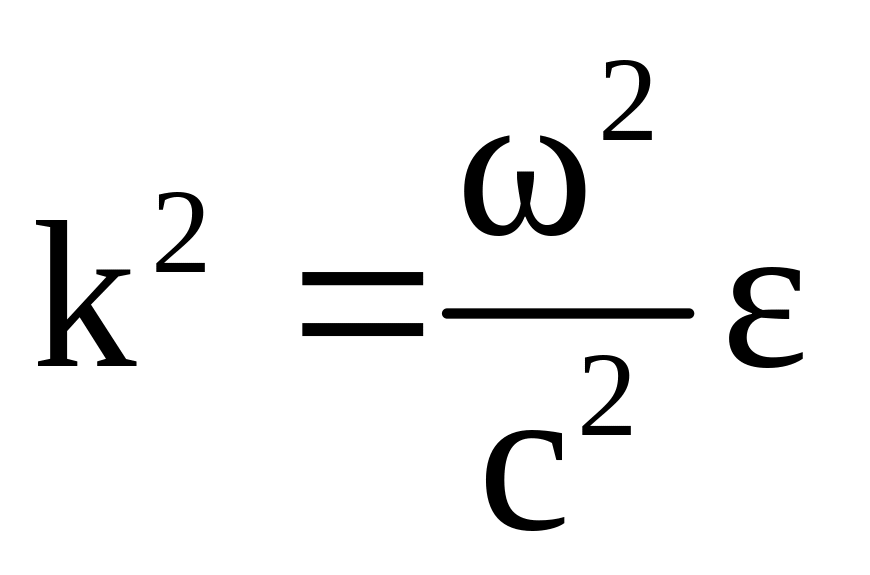Координатную плоскость xy расположим в плоскости раздела. По отношению к координатам x и y задача является пространственно-однородной. Это означает, что тангенциальные компоненты волнового вектора всех трех волн – падающей, отраженной и преломленной – одинаковы. Из дисперсионного уравнения электромагнитных волн в каждой среде , Из равенства k_ox=k_1x=k_2x следует, что в первой среде

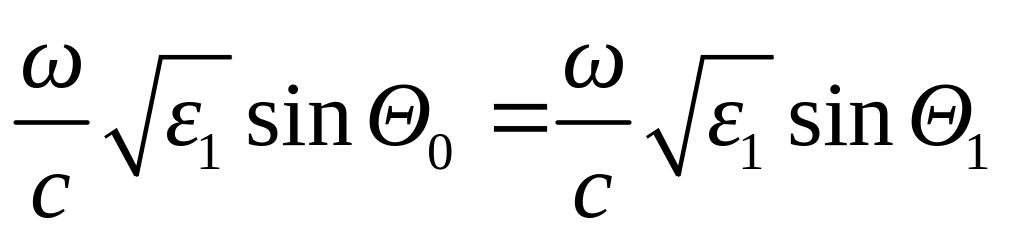
и _о=₁. (1)

Т.о., равенство угла падения углу отражения является прямым следствием сохранения тангенциальной компоненты волнового вектора падающей и отраженной волн. Во второй среде

. (2)

Эта компонента волнового вектора в поглощающей среде может оказаться величиной комплексной. Если вторая среда является прозрачной, то из (1) и (2) следуют простые законы, связывающие углы падения, отражения и преломления

_о= ₁ и 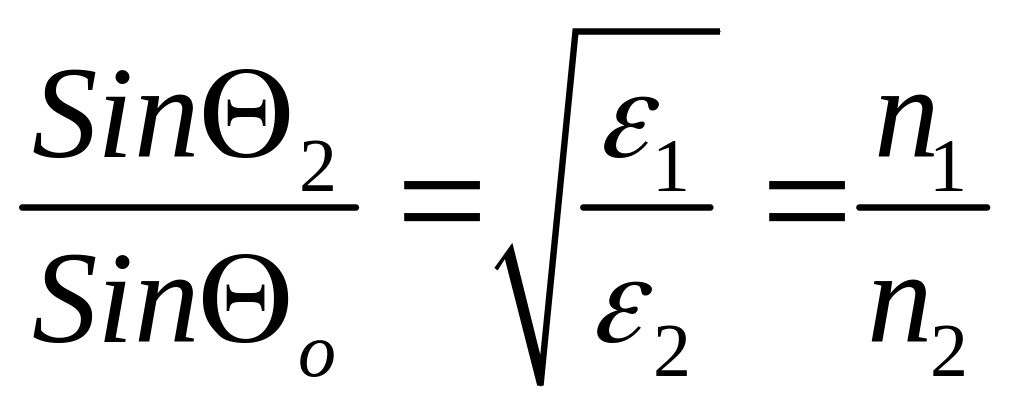. (3)

Из полученных выражений можно определить ход лучей, но эти формулы не говорят об их интенсивностях. Для того чтобы найти эти интенсивности, следует принять во внимание граничные условия на поверхности раздела (z=0):

, , , .

При этом мы рассмотрим отдельно два случая – когда электрическое поле лежит в плоскости падения или перпендикулярно к ней; тем самым мы рассматриваем и общий случай, когда может быть разложено на две такие компоненты.

Предположим сначала, что перпендикулярно к плоскости падения; из соображений симметрии очевидно, что тоже будет относиться и к полям и в отраженной и преломленной волнах. Вектор же лежит в плоскости xz. Граничные условия требуют непрерывности E_y и H_x, а из уравнений Максвелла имеем

.

Поле в среде I есть сумма полей падающей и отраженной волн, так что мы получаем два уравнения:

, (4)

Решая систему уравнений (4) относительно Е₁ и Е₂ найдем

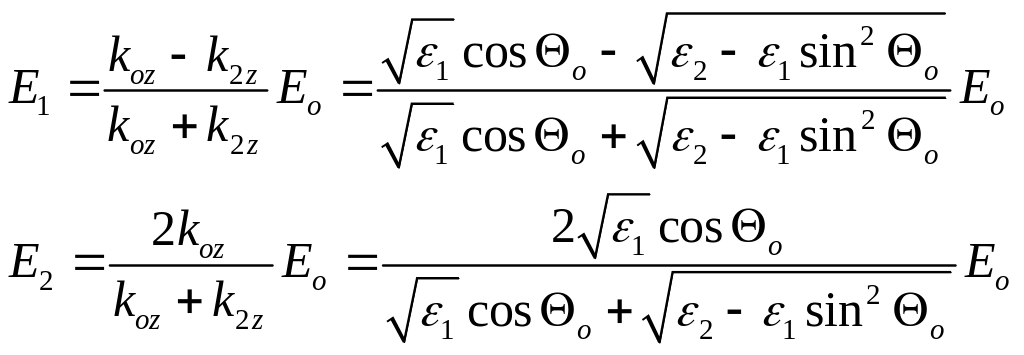(5)

Эти формулы называются формулами Френеля. В случае прозрачных сред, т.е. когда выполняются соотношения (3), формулы Френеля упрощаются

, (6)

Можно убедится, что граничные условия для D_n и B_n не дают новых результатов.

Аналогичным образом можно рассмотреть случай, когда Е лежит в плоскости падения; при этом удобнее производить вычисления для магнитного поля, перпендикулярного к плоскости падения. В результате получаются еще две формулы Френеля:

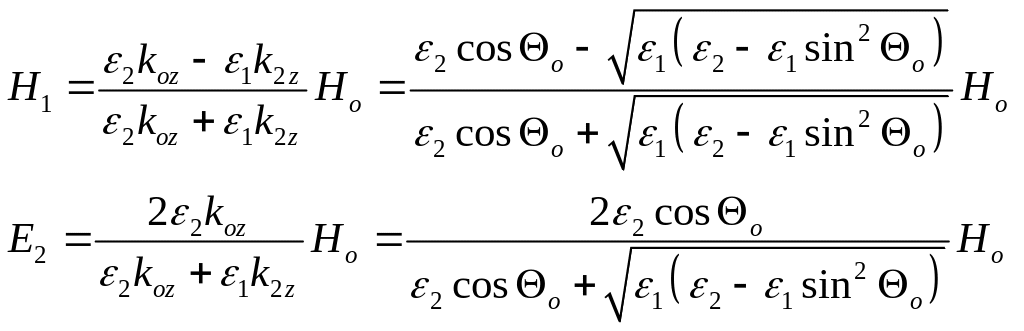. (7)

В прозрачных средах эти формулы примут вид

, . (8)

Коэффициент отражения R определяется как отношение среднего (по времени) отраженного от поверхности потока энергии к падающему потоку. Каждый из этих потоков дается средним значением z-компоненты вектора Пойтинга соответствующей волны

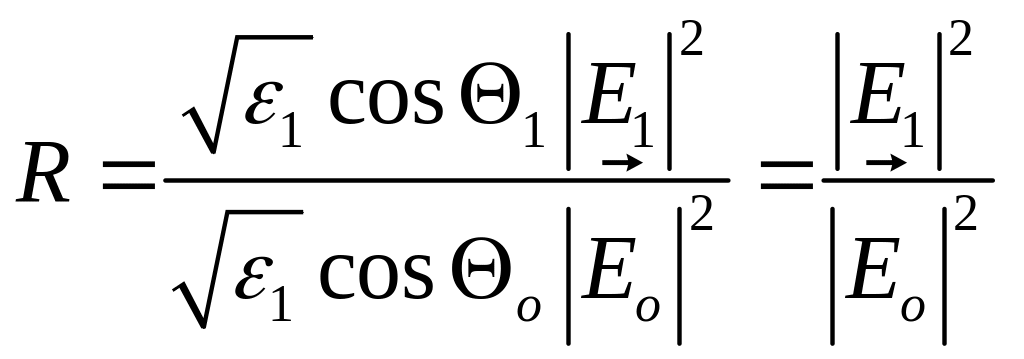. (9)

При нормальном падении (_о=0) оба случая эквивалентны и коэффициент отражения определяется формулой

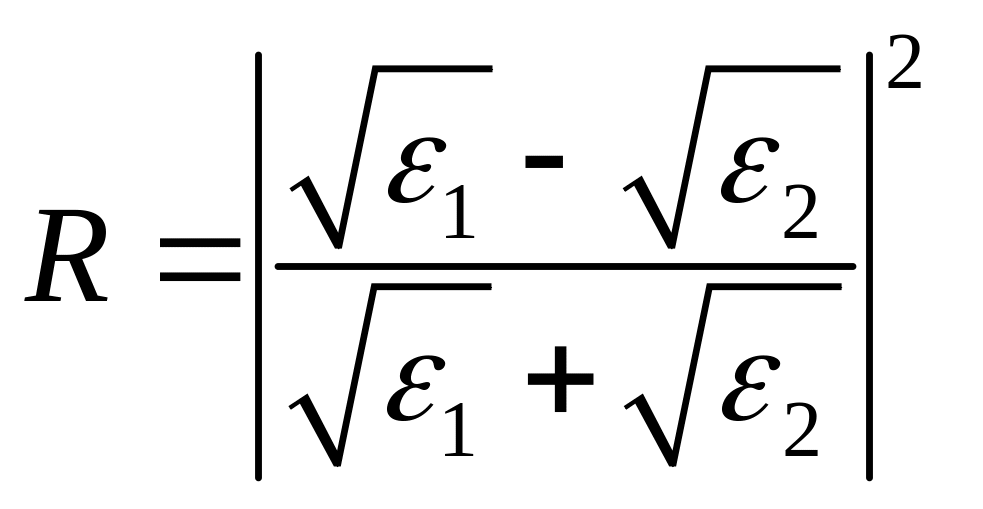. (10)

Если показатель преломления среды , то при падении волн на такую среду, например, из вакуума (₁=1) будем иметь

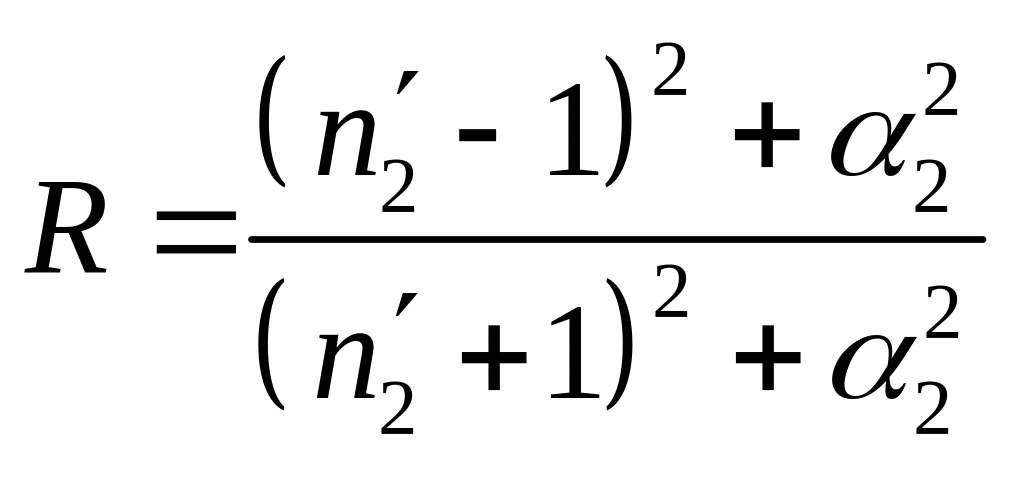. (11)

При наклонном падении, согласно (6) и (8)

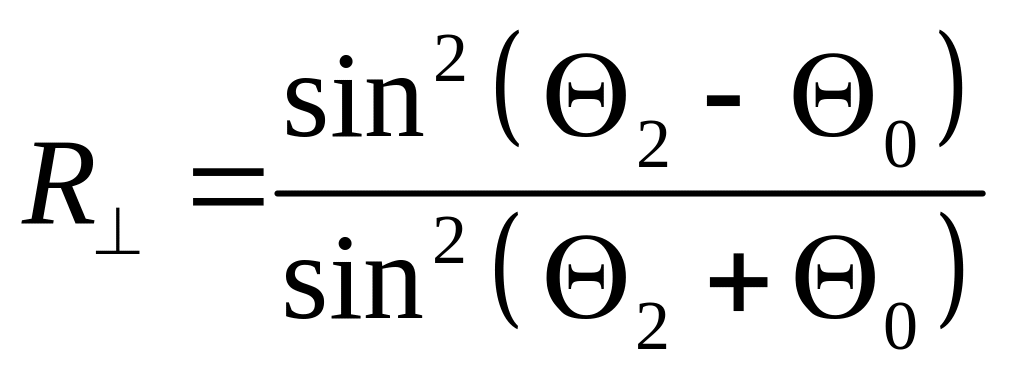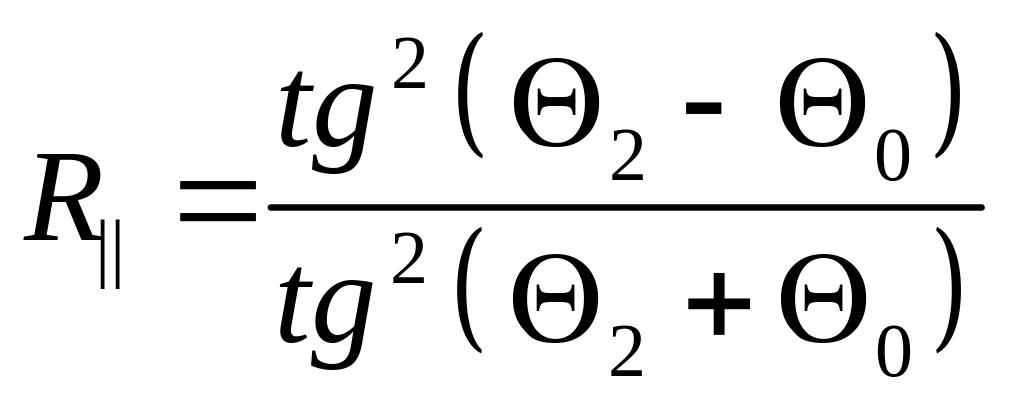, . (12)

Здесь и – коэффициенты отражения падающих волн, поляризованных, соответственно, перпендикулярно и параллельно плоскости падения.

Замечательным свойством обладает отражение света, падающего под таким углом _о, при котором _о+₂=/2 (отраженный и преломленный лучи при этом взаимно перпендикулярны).

Обозначим этот угол падения как _Б – угол Брюстера. Используя закон преломления получаем

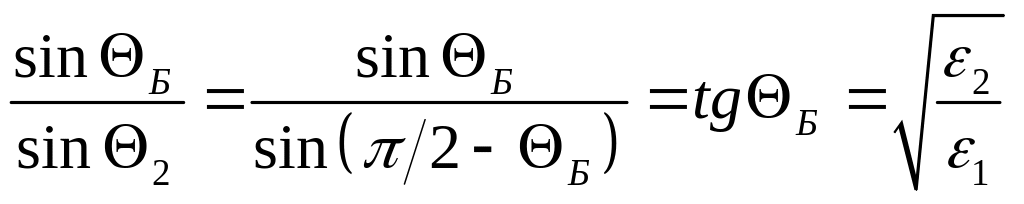(13)

При _о=_Б имеем и R_|| обращается в нуль. Поэтому при любой поляризации падающего под углом _Б пучка электромагнитных волн отраженные от среды II волны оказываются полностью поляризованными в плоскости, перпендикулярной плоскости падения. Преломленные же волны линейно-поляризованными не будут.

Другое важное явление, возникающее при падении электромагнитных волн на поверхность раздела двух сред – полное внутреннее отражение. Оно возникает при отражении от оптически менее плотной среды, т.е. при ₂<₁. Когда имеет место полное внутреннее отражение, то преломленная волна не проникает в оптически менее плотную среду: величины R_ и R_|| обращаются в единицу. Соответствующий угол падения _о=_r определяется из условия и равен

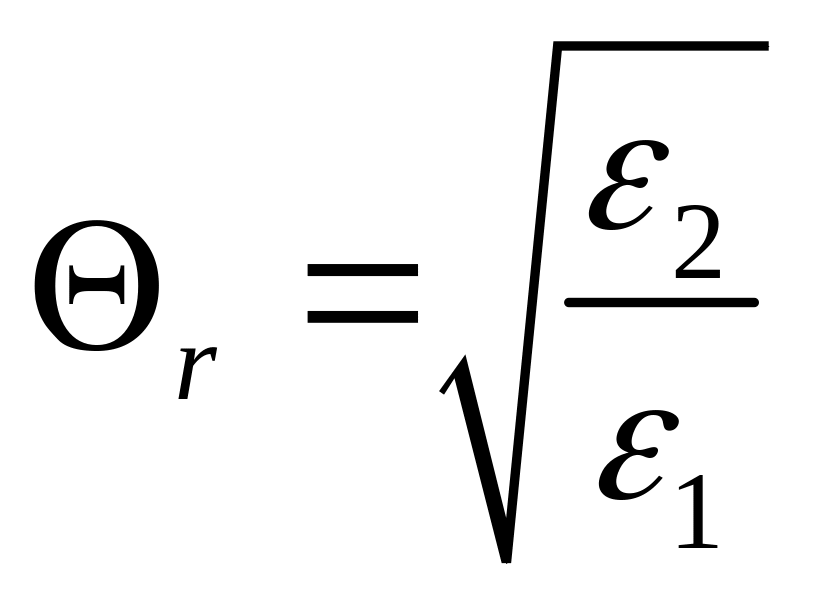, ₂  _1. (14)