Диэлектрическая проницаемость плазмы в магнитном поле

Магнитоактивными называются анизотропные гиротропные среды, приобретающие эти свойства под действием постоянного магнитного поля. Тензоры диэлектрической или магнитной проницаемости таких сред несимметричны. В магнитоактивной непоглощающей среде тензор ε_ij - эрмитов:

. (1)

Действительная и мнимая части ε_ij - должны быть соответственно симметричной и антисимметричной:

. (2)

Такими же свойствами обладает и μ_ij. Если тензором является диэлектрическая проницаемость, а μ_ij — скаляр, то среда называется гироэлектрической. Примером может служить плазма, находящаяся в постоянном магнитном поле (земная ионосфера, солнечная корона и т. п.). Если тензором является магнитная проницаемость, то среда называется гиромагнитной.

Перейдем к рассмотрению свойств магнитоактивной плазмы. Для того чтобы в явном виде получить выражение для тензора диэлектрической проницаемости, нужно рассчитать движение электронов, ионов и нейтральных молекул плазмы в присутствии постоянного магнитного поля и переменных волновых полей. При анализе произвольных движений в плазме исходными являются уравнения электромагнитного поля и кинетические уравнения для электронов, ионов и нейтральных молекул. Подобная система уравнений очень сложна, и поэтому большое значение приобретают различные приближенные решения динамической задачи. Если частота волны удовлетворяет условию

(3)

( - собственная частота вращения ионов в магнитном поле H, М – масса иона) то при определении поляризации среды можно считать ионы неподвижными и учитывать только движение электронов. Волны, для которых это условие выполнено, будем называть высокочастотными. Если, кроме того,

ω >> ν (4)

(где ν — эффективная частота соударений электронов с молекулами и ионами), то токи смещения в среде должны преобладать над токами проводимости. При выполнении условия в поле электромагнитной волны происходит пространственное разделение зарядов; это приводит к возникновению сильных электрических полей, стремящихся сблизить заряды. В результате возникают колебания плотности заряда с плазменной частотой

.

В низкочастотной области, когда , плазму можно рассматривать как электрически нейтральный проводящий газ, находящийся в электромагнитном поле. Механическое движение плазмы описывается в этом случае как движение сплошной проводящей среды (жидкости или газа) с помощью обычных гидродинамических переменных: плотности, скорости, давления. Иногда роль ионов оказывается существенной и при более высоких частотах. Например, при поперечном по отношению к внешнему магнитному полю распространении волн влиянием ионов можно пренебречь только при условии

,

- собственная частота вращения электрона в магнитном поле.

Будем считать, что условия (3), (4) выполнены и плазма представляет собой однородный ионизованный газ, в единице объема которого содержится N электронов. Условие (4) позволяет пренебречь токами проводимости и считать, что полный ток в среде равен току смещения, т.е.

. (5)

Здесь и в дальнейшем мы предполагаем, что все величины изменяются по времени по гармоническому закону. Поскольку D = Е + 4πР, с учетом (5) получим

. (6)

Здесь использованы следующие обозначения:

. (7)

Для определения величины V (а следовательно, и компонент тензора диэлектрической проницаемости) воспользуемся уравнением движения электрона

. (8)

H - внешнее постоянное магнитное поле создающее анизотропию плазмы. С учетом (7) уравнение (8) перепишем в виде

(9)

где . Выберем систему координат, ось z которой совпадает с направлением Н. Тогда величина , и мы получим следующую систему уравнений для определения компонент вектора V:

. (10)

Записав с помощью (10) компоненты вектора V = (V_x, V_y, V_z) и подставляя их в уравнение (6), получим выражение для компонент вектора D:

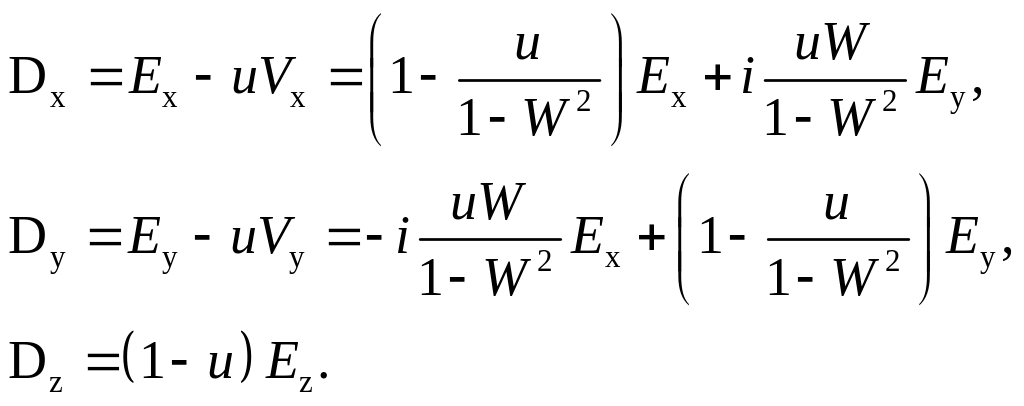(11)

Отсюда следует, что тензор диэлектрической проницаемости в выбранной системе координат имеет вид

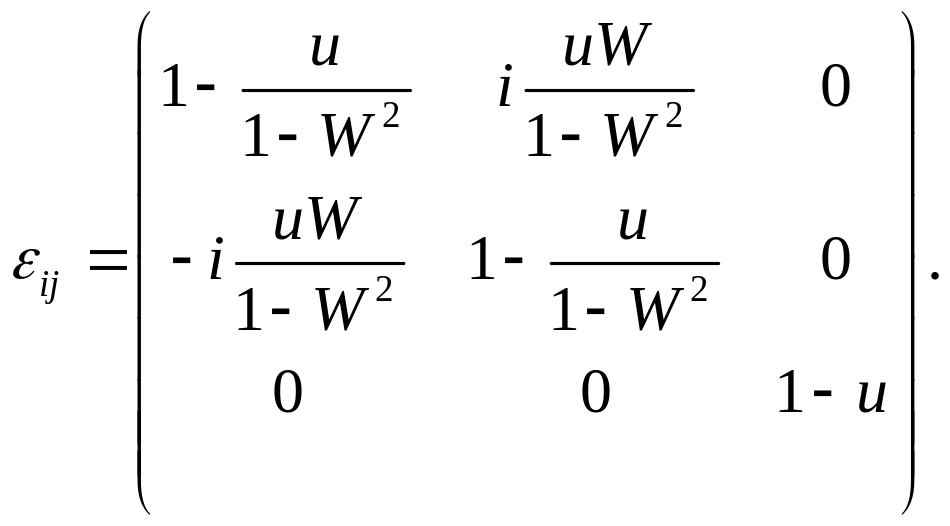(12)

Тензор ε_ij не является действительным (несмотря на то, что поглощение при выводе (12) не учитывалось). Его компоненты связаны соотношением , т. е. тензор эрмитов.

В направлении оси z векторы D и E параллельны, но в плоскости х, у векторы D и Е параллельны только для волн, имеющих круговую поляризацию. Действительно, из (11) получаем

. (13)

Комбинация , как следует из (12), является действительной величиной. Отсюда можно сделать заключение, что в магнитоактивной среде нормальные волны имеют круговую (или. эллиптическую) поляризацию. Согласно (12) с учетом введенных обозначений (7)

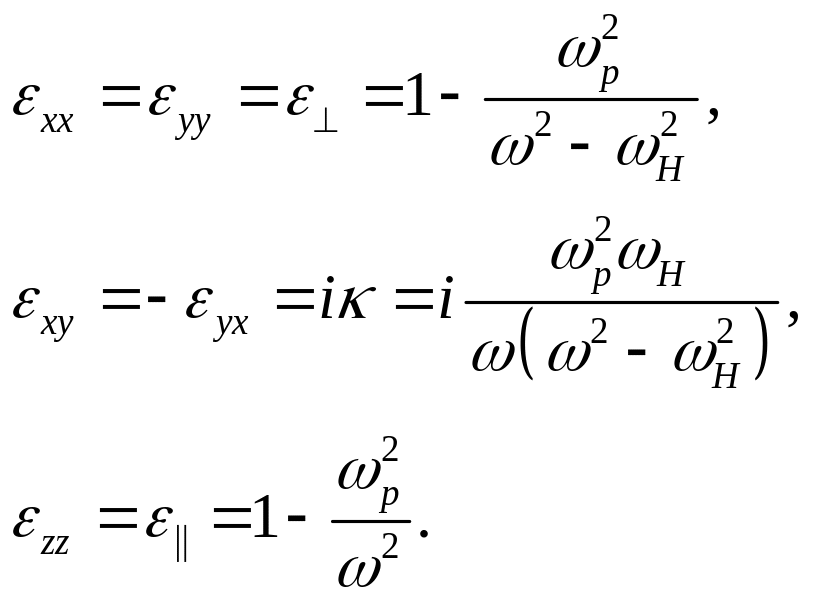(14)

Из формул (14) видно, что второй характерной особенностью магнитоактивной среды является существование резонансных явлений при . Действительно, при некоторые компоненты тензора ε_ij - обращаются в бесконечность. Необходимо, однако, иметь в виду, что при расчете тензора ε_ij мы не учитывали диссипативных процессов. Если учесть потери энергии из-за соударений увлекаемых волной электронов с ионами и нейтральными молекулами, то компоненты тензора диэлектрической проницаемости будут иметь следующий вид:

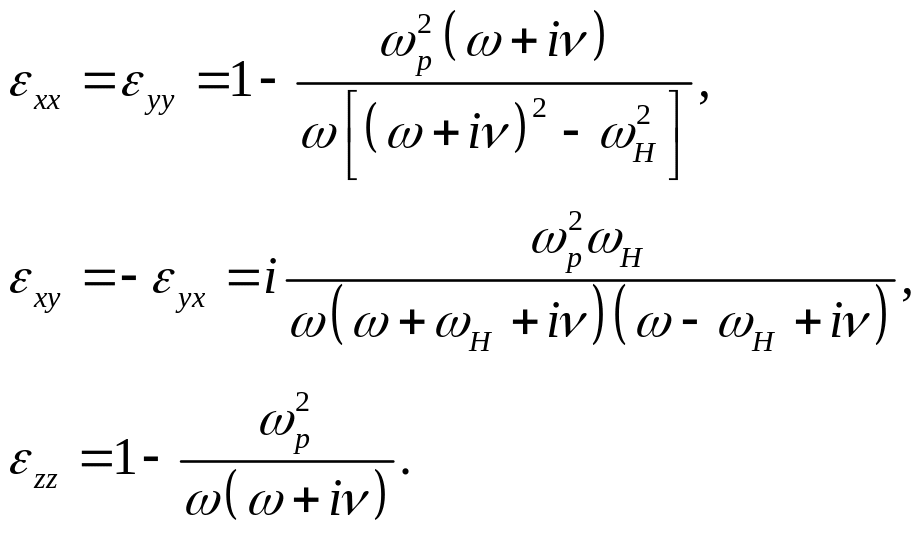
Тензор диэлектрической проницаемости в этом случае может быть представлен в виде

где , . С учетом соударений резонансные явления обычно проявляются в резком возрастании поглощения «необыкновенной» волны, направление вращения вектора Е в которой совпадает с направлением вращения электронов в магнитном поле Н.

Когда частота приближается к резонансной, радиус орбиты электрона увеличивается; следовательно, электрон проходит в среде больший путь и число его соударений с ионами и молекулами за единицу времени возрастает.

Если учесть движение ионов в поле волны, пренебрегая соударениями, то компоненты тензора примут вид

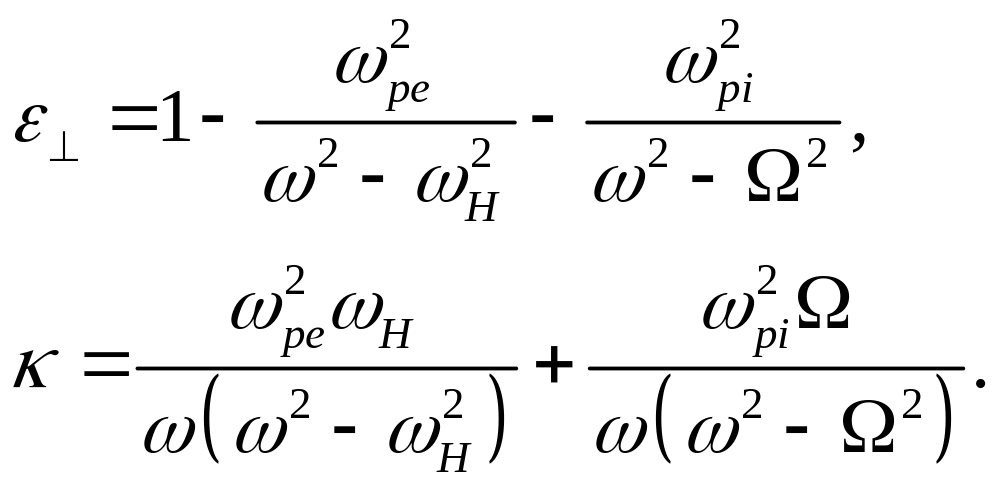(15)

В высокочастотном приближении, когда , из (15) следует прежний результат (14). В пределе низких частот имеем

Если считать, что плазма полностью ионизована, то N(m+M) =ρ — плотность среды. Следовательно,

. (16)