4.3. Точность оценивания параметров

О точности и надежности точечной оценки можно судить по величине доверительного интервала и соответствующей ему доверительной вероятности. Однако приведенные в разд. 4.2 формулы, как указывалось, относятся к случаю, когда наблюдаемая величина подчинена нормальному закону. Если выборка достаточно велика и оценка имеет вид суммы, то эти формулы можно применять и для наблюдаемых величин, распределенных отлично от нормального закона. Однако когда число наблюдений существенно ограничено, распределение используемых статистик отличается от нормального и связанных с ним

распределений χ² и Стьюдента, что приводит к ошибкам при вычислении вероятностей их попадания в доверительный интервал. В разд. 2 приведен алгоритм, позволяющий находить распределение любых статистик на основе генерации псевдовыборок произвольного объема. Согласно этой процедуре исследование точности оценивания параметров по выборкам малого объема можно осуществить следующим образом.

1.Задавшись распределением наблюдаемой случайной величины, генерируем N выборок объема п каждая. При этом N должно быть достаточно велико (N> 1000), а n, наоборот, незначительно ( 5; 10;15,…)

2.Для каждой выборки вычисляем оценку исследуемого параметра, например,

3.По множеству оценок параметра строим гистограмму. При до статочно большом N она должна хорошо отражать плотность распределения оценки, полученной по выборке объема п .

4.Задаемся величиной доверительного интервала (например, α % от значения параметра) и по гистограмме находим вероятность попадания в этот интервал, располагая его симметрично относительно параметра. Это будет доверительная вероятность γ для α-процентного ^{доверительного интервала.}

5. Вычисляем по формулам разд. 4.2.2 доверительную вероятность

^{для того же интервала и сопоставляем результаты.}

6. На основе проведенных исследований для разных объемов для случайных выборок, делаем выводы о точности оценивания точечных параметров по выборкам небольшого объема.

4.4.Контрольные вопросы

1.Какие оценки параметров называются точечными?

2.. .Что такое состоятельность, эффективность и несмещенность точечных оценок?

3.В чем состоит метод статистических моментов?

4.Что такое сходимость по вероятности (поясните это понятие, используя полученные Вами результаты)?

5.Какие оценки называются интервальными?

6.Что такое доверительный интервал, доверительная вероятность?

7.Что такое χ² -распределение?

8.Чему равны параметры χ² -распределения?

9.Охарактеризуйте распределение Стьюдента.

10.Объясните, почему способы вычисления доверительных интервалов, приведенные в разд. 4.2.1 и 4.2.2, применимы лишь к нормально распределенным величинам?

11.Почему в выборках малого объема распределение оценки, имеющей форму суммы, отличается от нормального? Приведите примеры.

12.Как вычисляется доверительный интервал и доверительная вероятность по экспериментальным данным?

13.Из каких соображений выбирается число N исследуемых выборок (число оценок)?

14.Какие выводы Вы можете сделать по окончании эксперимента по способу исследования точности оценивания, предложенного в разд. 4.3?

5. ПРОВЕРКА ПРОСТЫХ СТАТИСТИЧЕСКИХ ГИПОТЕЗ О ПАРАМЕТРАХ РАСПРЕДЕЛЕНИЯ ПО ОТНОШЕНИЮ

ФУНКЦИЙ ПРАВДОПОДОБИЯ

Метод последовательного анализа. Проверка статистических гипотез — одна из важных задач теории статистических решений. Гипотеза называется простой, если она определяет единственным образом распределение случайной величины, и сложной, если она определяет его в некоторой области.

Рассмотрим задачу проверки простой гипотезы с единственной альтернативой о параметре функции распределения случайной величины. Пусть распределение случайной величины X определено не полностью, и о некотором параметре а этого распределения мы выдвигаем гипотезу, что он равен a₀ (альтернатива состоит, в том что он равен a₁). Пусть по результатам независимых наблюдений X получена случайная выборка объемом n: {x₁,x₂,…,x_n}.

Для оценки правдоподобия гипотезы построим функцию правдоподобия для гипотезы a=a_0:

если X – непрерывная случайная величина,

(5.1)

если X – дискретная случайная величина,

(5.1΄)

Из (5.1΄) видно, что когда X дискретна, функция правдоподобия выражает вероятность того, что в результате выборки объема n будут получены значения именно x₁,x₂,…,x_n , если справедлива гипотеза a₀. Если X непрерывна, то функция правдоподобия пропорциональна этой вероятности.

Аналогичным образом можно построить функцию правдоподобия для альтернативной гипотезы: .

Метод отношения функций правдоподобия предписывает следующее, если принимается гипотеза a₀, в противном случае гипотеза a₀ отвергается (принимается альтернативная гипотеза a₁). Иными словами, принцип максимального правдоподобия предлагает принимать из двух альтернатив ту, при которой полученная случайная выборка не менее, чем в с раз представляется более вероятной. Этому методу можно дать более общее описание.

Рассматривается отношение функций правдоподобия

(5.2)

Область его возможных значений на две: область допустимых значений R₁, где

Если найденное по случайной выборке значение отношения правдоподобия попадает в область допустимых значений ( ), то принимается гипотеза a₀, если же отношение правдоподобия попадает в критическую область( ), гипотеза a₀ отвергается и принимается альтернативная гипотеза a₁.

В силу случайной выборки значение критерия также является случайной величиной, зависящей от параметра a. Пусть распределение нам известно. Тогда

(5.3)

есть вероятность того, что мы отбросим правильную гипотезу, т.е совершим ошибку первого рода. Аналогично

(5.4)

есть вероятность принять неверную гипотезу, т.е совершить ошибку второго рода.

Из формул (5.3) и (5.4) видно, что выбирая границу допустимой и критической области (т.е. точку С), мы управляем величинами вероятностей ошибок первого и второго рода. Именно поэтому С часто принимают отличной от единицы.

Использование описанного метода имеет тот недостаток, что объем выборки определяется заранее и уже после определяется достигнутая точность, т.е. ошибки первого и второго рода. Это обстоятельство учтено в предложенном А.Вальдом методе последовательного анализа [7]. Сущность его состоит в следующем. Все множество значений ζ делится не на две, а на три области: область допустимых значений R₁, критическая область R₂ и некоторую промежуточную область R₃. Значение ζ вычисляются последовательно после каждого наблюдения. Если после n-го (n=1,2,…) наблюдения получаем , то гипотеза a₀ принимается, и эксперимент на этом заканчивается; если , то гипотеза a₀ отвергается, и эксперимент также прекращается. Если же , то никого решения не принимается, и эксперимент продолжается далее (т.е. делается (n+1)-е наблюдение и оценивается принадлежность областям R_1, R₂ и R₃).

Вероятности ошибок первого и второго рода в этом случае соответственно будут

(5.5)

Из существа метода ясно, что вероятности ошибок при фиксированных областях R₁ и R₂ зависит от числа проведенных наблюдений. Рассеивание ξ убывает с ростом объема выборки n, и α и β, естественно, уменьшаются. Так как вероятности ошибок первого и второго рода однозначно связаны с областями R₁ и R₂, то разумно поступить следующим образом: зафиксировать допустимы е величины вероятностей ошибок первого и второго рода и для каждого n-го наблюдения определить соответствующие им области R_1n и R_2n (следует заметить что в общем случае задача отыскания границ этих областей весьма сложна).

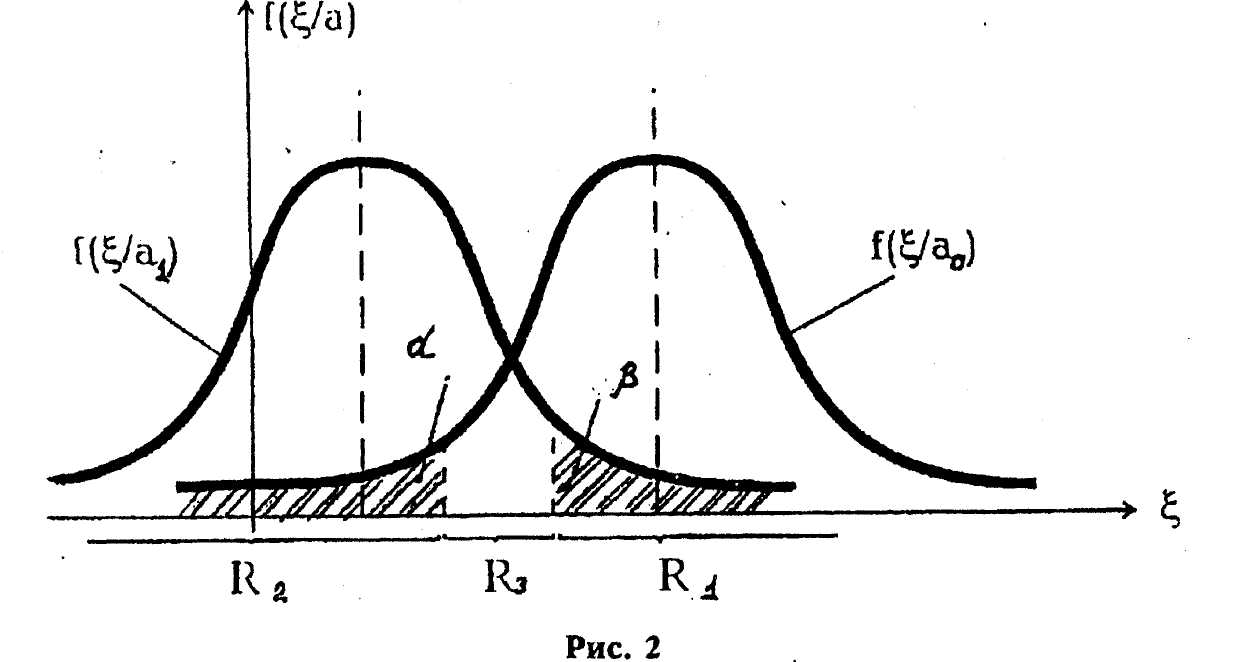
На рис.2 иллюстрируется области R_1n , R_2n и R_3n, а также вероятности ошибок первого и второго рода.

Применение метода последовательного анализа позволяет в среднем существенно сократить число наблюдений над случайной величиной (объем выборки) при сохранении той же точности решения о правдоподобии гипотезы. При практическом использовании изложенного метода часто бывает удобнее пользоваться не величиной ξ, а ее логарифмом.