4.2. Вычисление интервальных оценок
Рассмотрим вычисление интервальных оценок дисперсии и математического ожидания нормально распределенной величины X.
4.2.1.Интервальная оценка дисперсии
Обратимся к статистике (4.8) и несколько преобразуем ее:
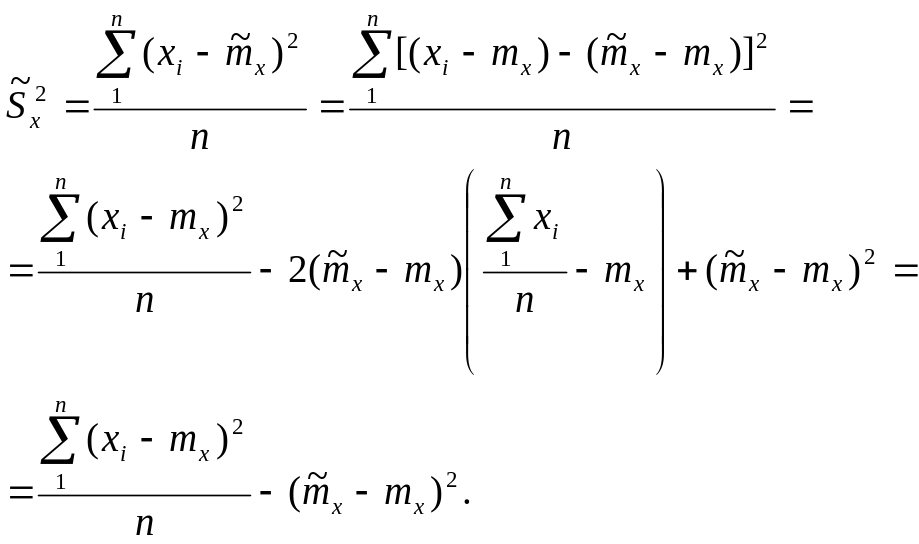
Умножим полученное выражение на
где
– оцениваемый параметр:
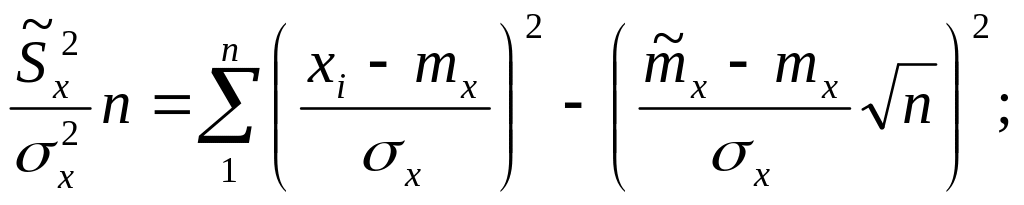(4.13)
Случайная величина
имеет нормированное нормальное
распределение. Случайная величина
также
имеет нормированное нормальное
распределение, так как оценка
,
вычисляемая по формуле (4.6), имеет
нормальное распределение с параметрами
и
Следовательно, случайная величина
представляет собой сумму квадратов
независимых нормированных нормально
распределенных величин. Число слагаемых
равно n-1. Значит
имеет
– распределение с r=ĉ
степенями свободы:
(4.13)
Напишем вероятность того, что
отношение
будет заключено в интервале [ a,
b ] :
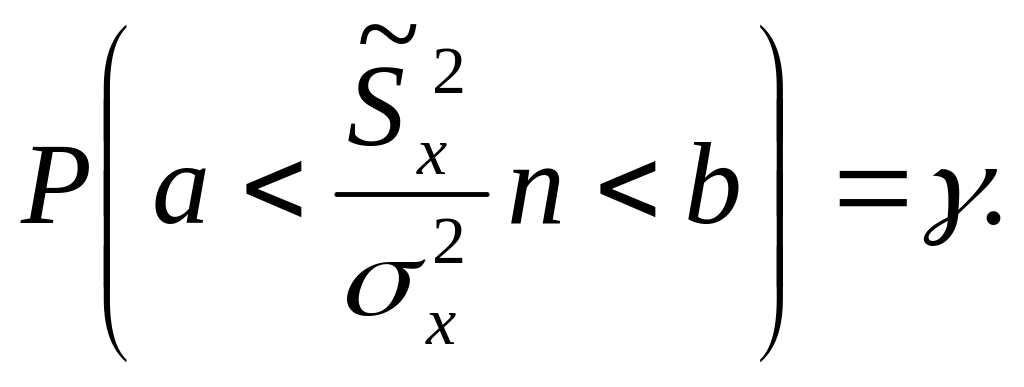
Пользуясь таблицами
– распределения с n-1
степенями свободы, найдем границы a
и b, обеспечивающие
минимальное значение интервала при
заданной вероятности γ. Обозначим их
и
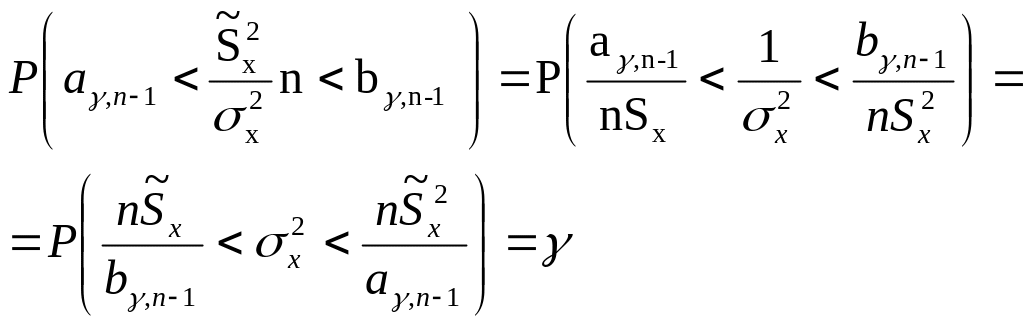
или
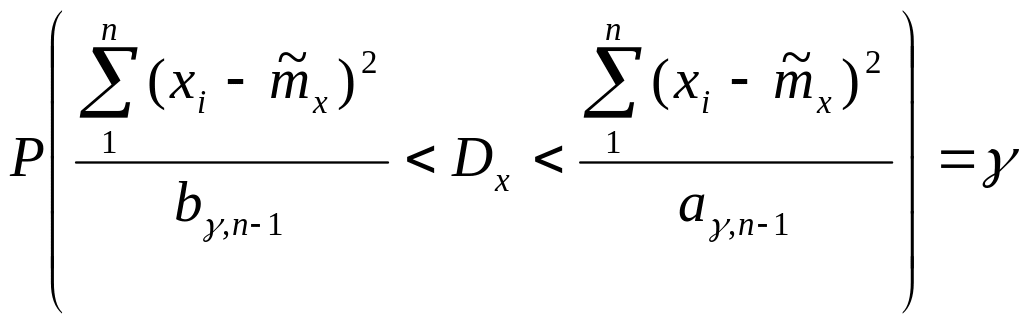(4.14)
Следовательно, с вероятностью
можно утверждать, что случайный интервал
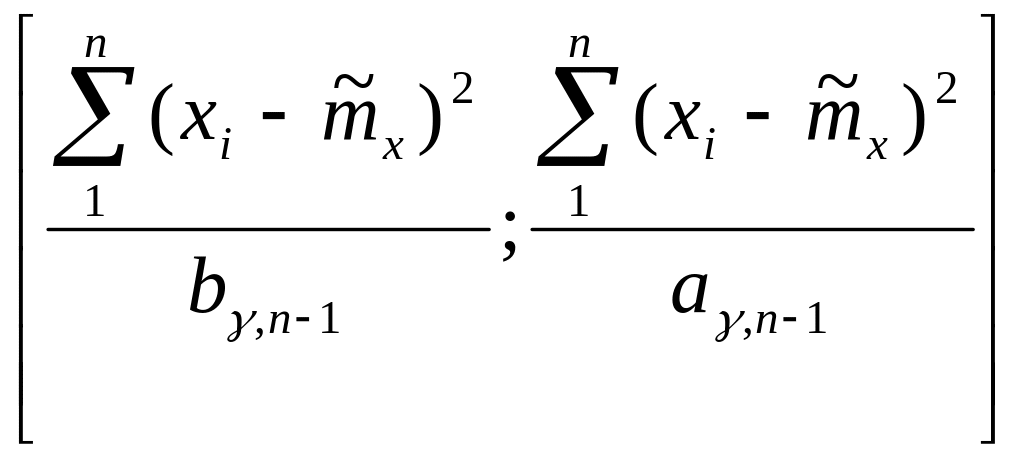накроет оцениваемый параметр D
x. Таким образом,
задача о вычислении доверительного
интервала для дисперсии нормально
распределенной величины решена. Наиболее
просто границы
и
находить из соотношений
Этот способ хотя и не обеспечивает минимальность доверительного интервала, но удобен для практического использования.
Соотношение (4.13) позволяет вычислить дисперсию оценки
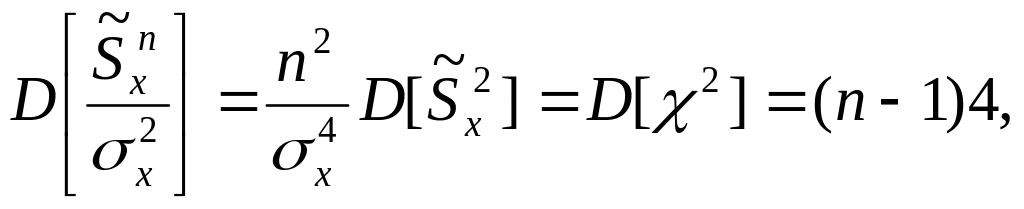
откуда
(4.15)
Если математическое ожидание наблюдаемой
величины X известно (т.е.
)
, то, как нетрудно видеть из вывода,
отношение
выражается суммой не (n-1)-го,
а n-слагаемых и число
степеней свободы
– распределения равно n,
что следует учитывать при обращении к
таблицам
– распределения.
4.2.2.Интервальная оценка математического ожидания
Введем случайную величину t, связывающую оцениваемое математическое ожидание с результатами эксперимента:
(4.16)
В числителе (4.16), как было показано в
разд.4.2.1, стоит нормированная нормально
распределенная величина, в знаменателе
– случайная величина, равная корню из
.
Следовательно, случайная величина t
подчинена распределению Стьюдента
(t-распределению) с n-1=r
степенями свободы. Дальше поступаем
аналогично разд. 4.2.1. Находим по таблицам
распределение Стьюдента интервал (
),
вероятность попадания в которой равна
доверительной вероятности γ:
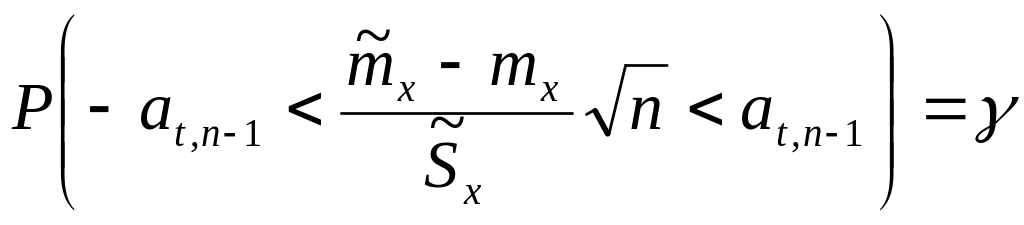
или после преобразований
(4.17)
где
и
находим по формулам (4.6) и (4.9).
Из (4.17) следует, что с доверительной
вероятностью γ случайный интервал
накрывает оцениваемый параметр m
x и, следовательно,
задача о вычислении доверительного
интервала для математического ожидания
решена.
Если дисперсия X известна,
то случайная величина t
подчинена нормальному закону распределения
с параметрами m x
= 0 и
=
1, и для нахождения границ a
и b надо обращаться к
интегралу вероятности Ф(x),
а не к распределению Стьюдента.