5.1. Проверка гипотезы о математическом ожидании

нормально распределенной случайной величины

Проверяется гипотеза о том что математическое ожидание нормальной случайной величины равно m_0, при единственной альтернативе m₁. Дисперсия σ² нормально распределенной случайной величины известна и выборка состоит из независимых элементов {x_1,x_2,…_,x_n}. Напишем сначала выражение для ln ξ_n в случае нормального распределения при независимых элементах выборки:

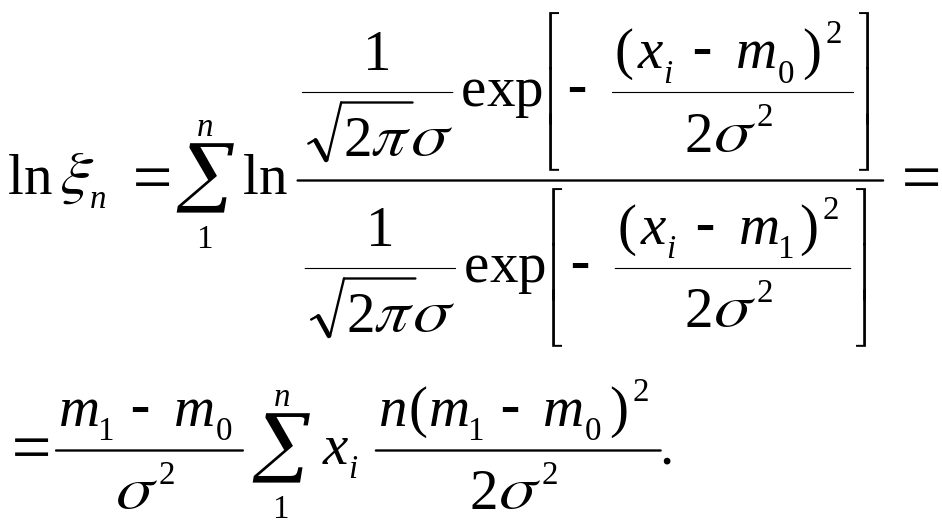(5.6)

Для простоты примем с=1, тогда m₀ принимается в случае Ln l(x₁,…,x_n)>0. Приравниваем (5.6) нулю, получаем граничную точку:

(5.6)

Следовательно, если m₀>m₁, то

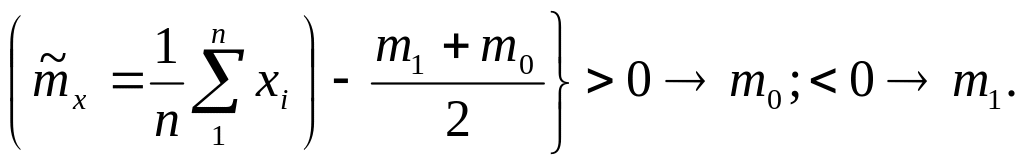(5.7)

Таким образом, процедура проверки гипотезы о математическом ожидании случайной величины сводится к сравнению среднего арифметического выборочных значений с некоторым порогом (если , то знак неравенства (5.7) меняется на противоположный).

В данной задаче в качестве критерия ξ принимается среднее арифметическое {x_i}, а область допустимых значений разделяется с критической в точке . Вероятности ошибок первого и второго рода запишутся:

Так как среднее арифметическое нормальной случайной величины распределено с то вероятности ошибок первого и второго рода

(5.8)

где Ф(x) – интеграл вероятности.

Если ошибки первого и второго рода не представляются равноценными (одинаково опасными), следует принять с≠1, что приведет к смещению границы допустимой и критической областей и перераспределению вероятностей α и β (α≠β). В этом случае граница допустимой R₁ и R₂ критической областей будет находится в точке а вероятности ошибок первого и второго рода соответственно равны:

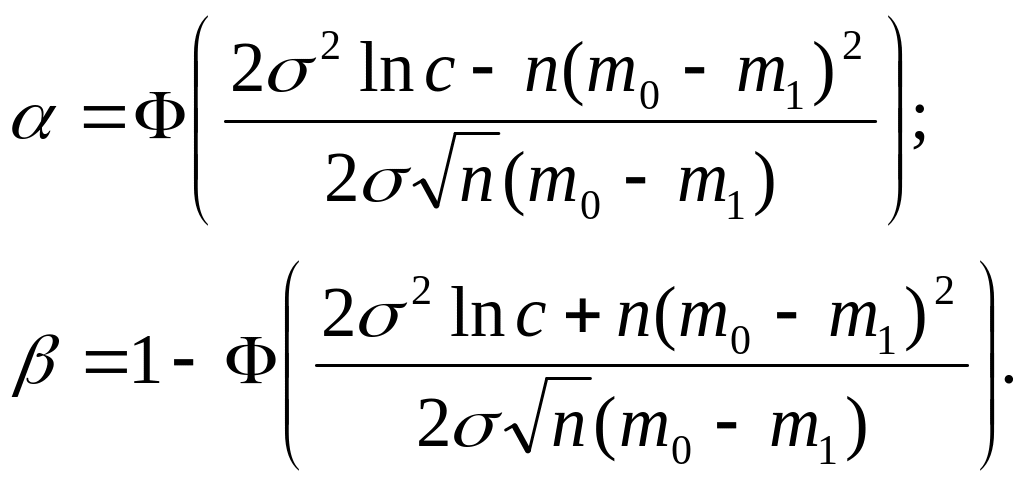(5.9)

При последовательном анализе, если в качестве критерия использовать, как и выше, оценку математического ожидания, то вероятности ошибок первого и второго рода на n-м шаге можно вычислить по формулам

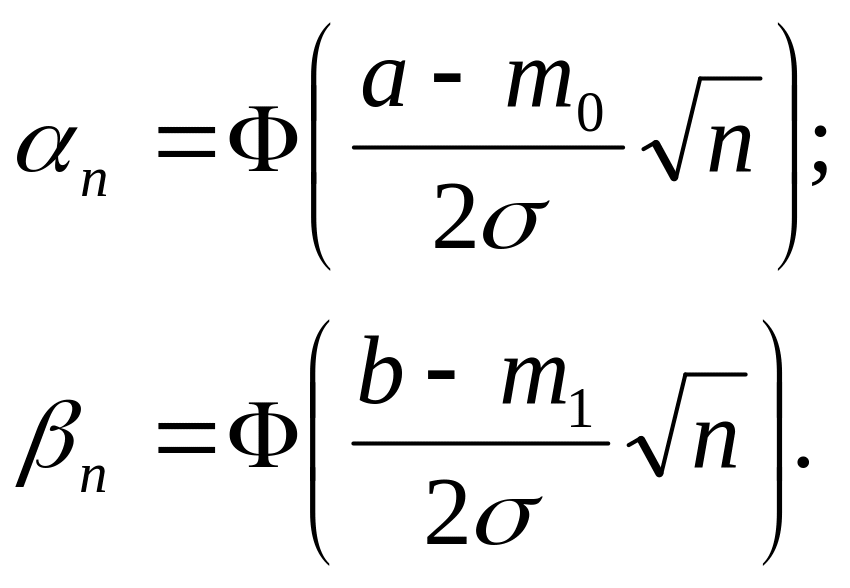(5.10)

При этом с увеличением числа шагов точность принимаемых решений, при неизменных границах a и b, будет расти. Если задаться точностью решений, т.е. вероятностями α и β, то из приведенных формул можно определить границы областей a_n и b_n, обеспечивающие эту точность на каждом шаге:

(5.11)

Если учесть, что α и β во всяком случае меньше, чем 0,5, то а и с ростом n границы областей сближаются, что способствует сходимости экспериментального процесса (рис. 2).

5.2. Проверка гипотезы о дисперсии нормально распределенной

случайной величины

Пусть среднее значение нормально распределенной случайной величины равно m, а относительно ее дисперсии выдвигается гипотеза, что она равна σ²₀, против альтернативы σ²₁,. Логарифм отношения функции правдоподобия имеет вид

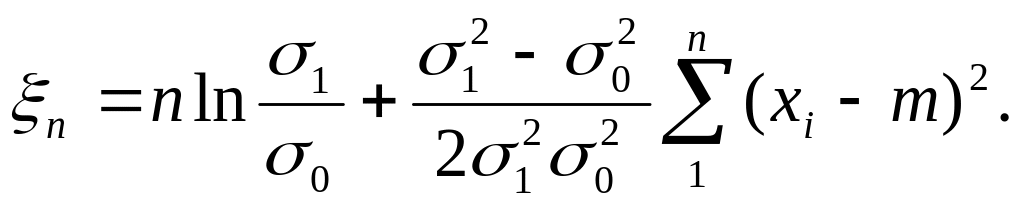(5.12)

Правило выбора решения при с=1 следующее.

Принимается, что дисперсия σ²₀, если при σ₁> σ₀

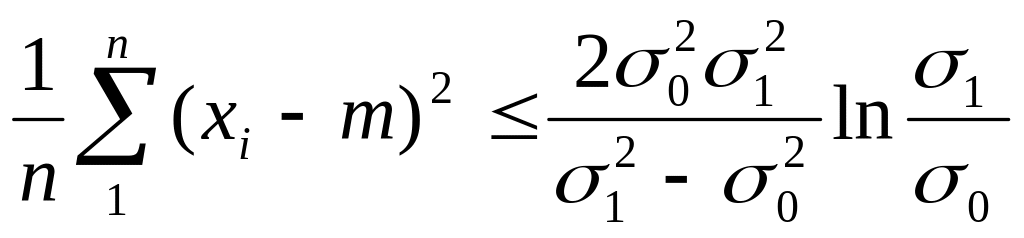(5.13)

и принимается, что дисперсия , если выполняется неравенство, противоположное (5.12).

Сумма квадратов нормированных нормально распределенных случайных величин имеет χ²-распределение с n степенями свободы и с помощью таблиц этого распределения можно найти вероятности ошибок первого и второго рода:

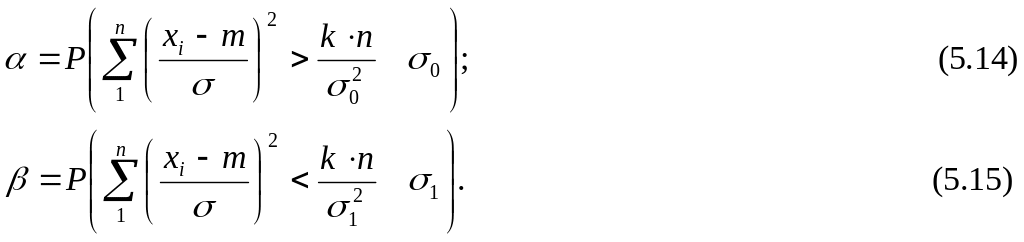
При последовательном анализе для заданных вероятностей ошибок α и β и σ₁> σ₀ принимается:

дисперсия нормальной случайной величины равна σ₀², если для наблюдаемой выборки

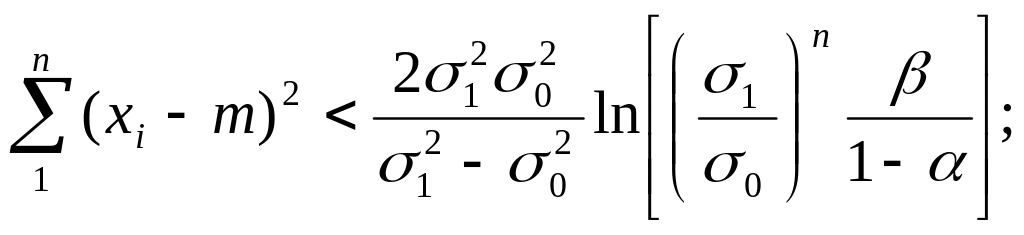(5.16)

дисперсия равна , если не выполняется ни одно из неравенств (5.16) или (5.17), т.е.

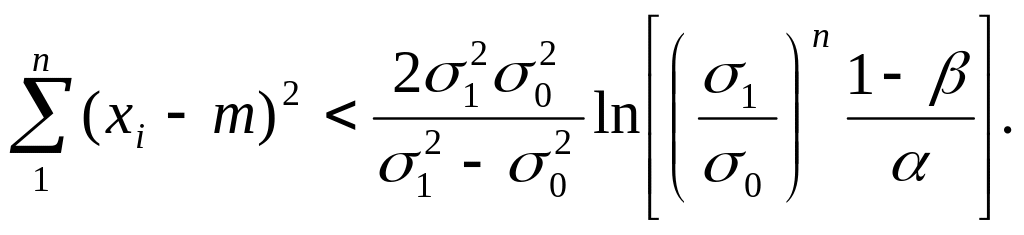(5.17)

Наблюдения продолжаются, если не выполняются ни одно из неравенств (5.16) или (5.17), т.е.

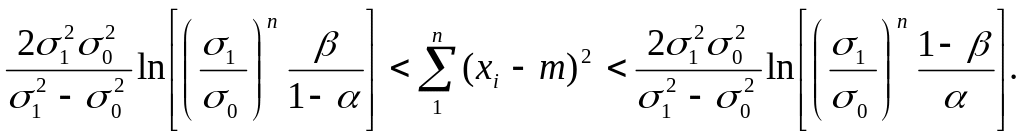(5.18)

Вывод неравенств (5.16) и (5.17) изложен в работе [5]. Из (5.16)-(5.17) видно, что границы областей R₁ и R₃ и R₂ и R₃ являются линейными функциями номера наблюдения.