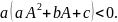МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАІЇНИ
ГИМНАЗІЯ №4
НАУКОВО-ДОСЛИДНИЦЬКА РОБОТА
На тему: розв’язування нестандартних рівнянь
Виконав:Яценко Олексій
Керівник:_____________
Миколаїв
2012
Квадратні рівняння
Квадратним
називається рівняння виду ax2
+
bx
+ c
=
0,
де
a,
b,
c
– фіксовані
дійсні числа, a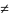 0.
0.
Якщо хоч один із коефіцієнтів b або c дорівнює нулю, квадратне рівняння називається неповним.
Розглянемо, як розв’язуються неповні квадратні рівняння:
а)
якщо c=0,
b≠0,
тоді ax2+bx=0
↔
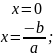 отже, рівняння має два корені: x1
=0,
x2=
-
отже, рівняння має два корені: x1
=0,
x2=
-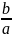 ;
;
б)
якщо
b
= 0, c
≠ 0, тоді
ax2
+ c
=
0, x2
=
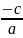 , причому при
, причому при
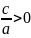 рівняння не має розв’язків, якщо ж
рівняння не має розв’язків, якщо ж
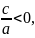 рівняння має два розв’язки:
рівняння має два розв’язки:
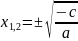 ;
;
в)
якщо
 тоді
тоді
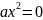 і
і
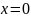 .
.
Приклади
Розв’язати рівняння

*
Відповідь:
 .*
.*
2.
Розв’язати
рівняння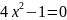 .
.
*
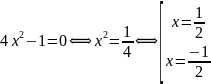
Відповідь: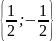 .*
.*
3.
Розв’язати
рівняння
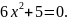
*
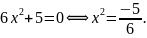 Відповідь:
розв’язків
немає. *
Відповідь:
розв’язків
немає. *
При
досліджені квадратного тричлена було
доведено, що квадратне рівняння має два
різних корені:
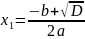 , де
, де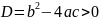 .
Якщо
.
Якщо
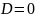 ,
то квадратне рівняння має один корінь
,
то квадратне рівняння має один корінь
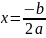 .
Нарешті, якщо
.
Нарешті, якщо
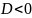 ,
розв’язків немає.
,
розв’язків немає.
Приклади
1.Розв’язати
рівняння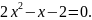
*
Послідовно
знаходимо:
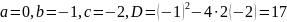 ;
;
17
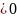 .
Рівняння має два розв’язки:
.
Рівняння має два розв’язки:
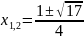 .
Відповідь:
.*
.
Відповідь:
.*
2.
Розв’язати
рівняння
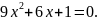
*
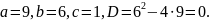 Рівняння має два розв’язки:
Рівняння має два розв’язки:
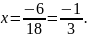 Відповідь:
Відповідь:
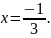 *
*
3.
Розв’язати
рівняння
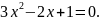
*
 Рівняння
не має розв’язків.
Відповідь:
розв’язків
немає.*
Рівняння
не має розв’язків.
Відповідь:
розв’язків
немає.*
4.
Розв’язати
рівняння
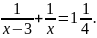
* Це рівняння не є квадратним, але зводиться до квадратного:
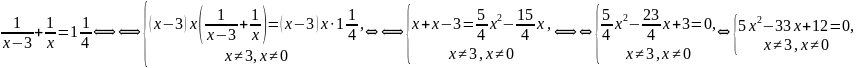
Розв’яжемо
рівняння
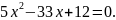 Маємо
Маємо
 .
.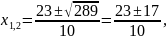 звідки
звідки
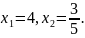 Маємо систему:
Маємо систему:
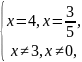
звідки
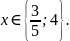 Відповідь:
Відповідь:
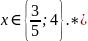
У випадку,
коли середній коефіцієнт
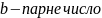 ,
формула розв’язків
квадратного рівняння спрощується.
Нехай
,
формула розв’язків
квадратного рівняння спрощується.
Нехай
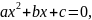 тоді
тоді
Приклади
5.
Розв’язати
рівняння

* Тут
 За
формулою маємо
За
формулою маємо
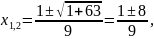 звідки
звідки
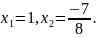 Відповідь:
*
Відповідь:
*
6.
Розв’язати
рівняння

* Це
рівняння з параметром не є квадратним,
але зводиться до квадратного. ОДЗ:
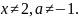 В
області допустимих значень маємо
В
області допустимих значень маємо
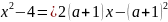 ,
або
,
або
 звідки
звідки
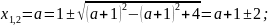 отже,
отже,
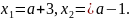 Згадаємо,
що
Згадаємо,
що
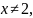 таким
чином,
таким
чином,
 звідки
звідки
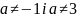 .
При
.
При
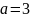 дане
рівняння має вигляд
дане
рівняння має вигляд
 ,
звідки
,
звідки
 Відповідь:
при
Відповідь:
при
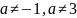 рівняння має два розв’язки:
рівняння має два розв’язки:
 при
при
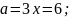 при
при
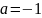 рівняння
втрачає сенс.*
рівняння
втрачає сенс.*
Нехай
квадратне рівняння
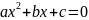 має
корені
має
корені
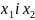 (можливо,
(можливо,
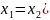 . Помітимо,
що
. Помітимо,
що
 .
.
У
випадку, коли
 Многочлени
Многочлени
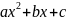 і
і
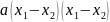 тотожно рівні. Отже,
тотожно рівні. Отже,
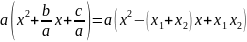 ,
звідки
виходять рівності
,
звідки
виходять рівності
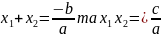 .
.
З
наведених міркувань випливає справедливість
теореми
Вієта:
для того щоб числа
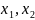 коренями
квадратного рівняння
,
необхідно і достатньо,щоб виконувалися
рівності
коренями
квадратного рівняння
,
необхідно і достатньо,щоб виконувалися
рівності
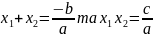 .
.
Зокрема,
якщо
-
корені квадратного рівняння
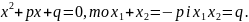
Приклади
Знайти суму квадратів коренів рівняння
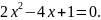
* Нехай
- корені даного рівняння (вони існують,
бо
 ).
Згідно з теоремою Вієта,
).
Згідно з теоремою Вієта,
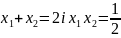 .
Тепер маємо
.
Тепер маємо
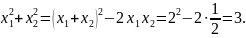 Відповідь: 3. *
Відповідь: 3. *
2.
При яких значеннях параметрів
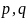 рівняння
рівняння
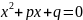 має корені
має корені
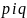 ,
якщо
,
якщо
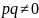 ?
?
* Згідно з теоремою Вієта, маємо систему рівнянь
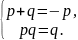
Враховуючи,
що
,
здобудемо
значення цих параметрів:
 .
.
ПЕРЕВІРКА.
Рівняння
 має корені
має корені
 ВІДПОВІДЬ:
ВІДПОВІДЬ:
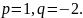 *
*
3.
При якому значенні
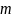 корені
рівняння
корені
рівняння
 задовольняють
умову
задовольняють
умову
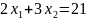 ?
?
* Згідно
з теоремою Вієта,
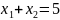 .
Маємо систему
.
Маємо систему
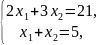
звідки
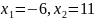 .
Тепер, згідно з теоремою Вієта, одержимо
.
Тепер, згідно з теоремою Вієта, одержимо
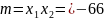 .
ВІДПОВІДЬ:
.
ВІДПОВІДЬ:
 *
*
4.
Обчислити суму обернених величин коренів
рівняння

* Нехай
 корені
даного рівняння. За теоремою Вієта
корені
даного рівняння. За теоремою Вієта

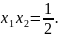
Далі
маємо
 ВІДПОВІДЬ:
ВІДПОВІДЬ:
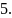 *
*
5.
При якому значенні параметра
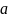 різниця
коренів рівняння
різниця
коренів рівняння
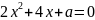 дорівнює
дорівнює
 ?
?
* Нехай
корені
даного рівняння і
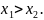 Згідно
з теоремою Вієта,
Згідно
з теоремою Вієта,
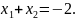 Маємо
систему
Маємо
систему
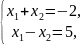
звідки
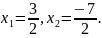 За
теоремою Вієта
За
теоремою Вієта
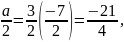 отже,
отже,
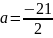
ВІДПОВІДЬ:
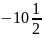 .
*
.
*
6.
Сума квадратів коренів рівняння
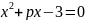 дорівнює
10. Знайти
дорівнює
10. Знайти
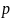 .
.
*
Нехай
корені
квадратного рівняння. Згідно з теоремою
Вієта,
 .
За
умовою,
.
За
умовою,
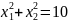 .
Отже,
.
Отже,
 звідки
звідки
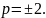 ВІДПОВІДЬ:
ВІДПОВІДЬ:
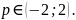 *
*
ЗАУВАЖЕННЯ.
Дискримінант даного рівняння
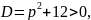 отже,
корені існують при будь якому
отже,
корені існують при будь якому
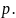
7.
Скоротіть дріб
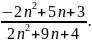
*
Якщо
корені квадратного тричлена
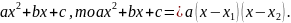 Розкладемо
чисельник і знаменник даного дробу на
множники.
Чисельник:
Розкладемо
чисельник і знаменник даного дробу на
множники.
Чисельник:
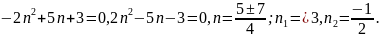 Отже,
Отже,
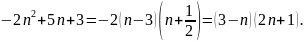 Знаменник:
Знаменник:
 Отже,
Отже,
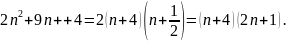 Тепер
маємо
Тепер
маємо
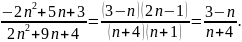 ВІДПОВІДЬ:
ВІДПОВІДЬ:
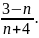 *
*
8.
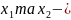 корені
рівняння
корені
рівняння
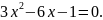 Скласти
квадратне рівняння, коренями якого є
числа
Скласти
квадратне рівняння, коренями якого є
числа
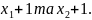
*
1-й
спосіб. Шукане рівняння має вигляд
 звідки
звідки
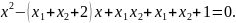
Згідно
з теоремою Вієта,
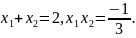 Тепер із рівняння маємо
Тепер із рівняння маємо
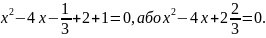 При бажанні одержати рівняння із цілими
коефіцієнтами, до множимо обидві частини
останнього рівняння на 3 і одержимо
При бажанні одержати рівняння із цілими
коефіцієнтами, до множимо обидві частини
останнього рівняння на 3 і одержимо
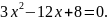
2-й
спосіб. Якщо
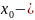 корінь рівняння
корінь рівняння
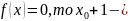 корінь рівняння
корінь рівняння
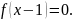 Отже, якщо
корені рівняння
Отже, якщо
корені рівняння
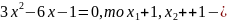 корені рівняння
корені рівняння
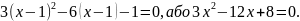 ВІДПОВІДЬ:
ВІДПОВІДЬ:
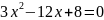 .
*
.
*
9.
корені
рівняння
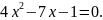 Скласти квадратне рівняння, коренями
якого є числа
Скласти квадратне рівняння, коренями
якого є числа
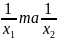 .
.
*
1-й
спосіб. За теоремою Вієта
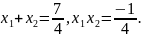 Нехай шукане рівняння має вигляд
,
тоді
Нехай шукане рівняння має вигляд
,
тоді


Отже,
шукане рівняння
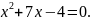
2-й
спосіб.
Якщо
 корінь
рівняння
корінь
рівняння
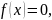 то
то
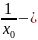 корінь
рівняння
корінь
рівняння
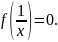 Тому
, якщо
корені
рівняння
Тому
, якщо
корені
рівняння
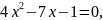 то
то
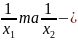 корінь
рівняння
корінь
рівняння
 ВІДПОВІДЬ:
*
ВІДПОВІДЬ:
*
10.
При якому значенні параметра
рівняння
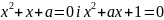 мають
спільний корінь?
мають
спільний корінь?
*
1-й
спосіб. Нехай перше рівняння має корені
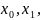 а
друге
а
друге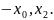 Згідно
з теоремою Вієта, маємо дві системи
Згідно
з теоремою Вієта, маємо дві системи
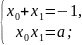
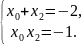
Ясно,
що жодне з чисел
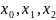 не
дорівнюють нулю. Розділивши другі
рівняння, маємо
не
дорівнюють нулю. Розділивши другі
рівняння, маємо
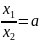 .
Віднявши від рівняння
.
Віднявши від рівняння
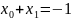 рівняння
рівняння
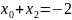 ,
одержимо, що
,
одержимо, що
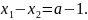 Тепер маємо систему
Тепер маємо систему
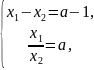
звідки
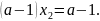
При
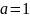 дані
рівняння не мають коренів, отже,
дані
рівняння не мають коренів, отже,
 ,
із останього рівняння одержимо
,
із останього рівняння одержимо
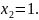 Тепер із рівняння
Тепер із рівняння
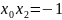 маємо
маємо
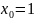 ,
з
рівняння
,
з
рівняння
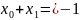 одержимо
одержимо
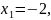 а
з рівняння
а
з рівняння
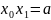 здобудемо
здобудемо
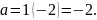
2-й
спосіб. Нехай
спільний корінь даних рівняння. Тоді
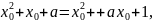 звідки
звідки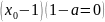 .
Оскільки
.
Оскільки
 З рівності
З рівності
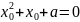 маємо
маємо
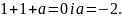
ПЕРЕВІРКА.
При
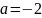 перше задане рівняння має корені
перше задане рівняння має корені
 , а друге
, а друге
 один корінь (або два однакових корені)
1. ВІДПОВІДЬ: при
.
*
один корінь (або два однакових корені)
1. ВІДПОВІДЬ: при
.
*
У деяких випадках можна розв’язати квадратне рівняння усно.
Теорема.
Якщо
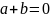 ,
то квадратне рівняння
,
то квадратне рівняння
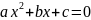 має
корені
має
корені

*
Дійсно,
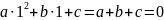 (за
умовою). Згідно з теоремою Вієта,
(за
умовою). Згідно з теоремою Вієта,
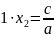 ,
звідки
,
звідки
 *
*
Наприклад,
рівняння
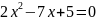 має
корені
має
корені
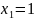 (бо
(бо
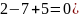 і (за теоремою Вієта)
і (за теоремою Вієта)
 Рівняння
Рівняння
 має корені
має корені
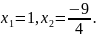 Рівняння
Рівняння
 має корені
має корені

Розглянемо ряд типових задач, пов’язаних із розв’язанням квадратних рівнянь з параметром.
Нехай
корені
рівняння
мають
різні знаки. Тоді
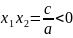 ,
тобто коефіцієнти
,
тобто коефіцієнти
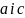 мають різні знаки. Ця умова є необхідною
і достатньою для того, щоб корені існували
і мали різні знаки, бо
,
оскільки
мають різні знаки. Ця умова є необхідною
і достатньою для того, щоб корені існували
і мали різні знаки, бо
,
оскільки
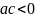 .
Ми довели теорему. Для
того щоб числа 0 знаходилось між коренями
рівняння
,
необхідно і достатньо, щоб виконувалася
умова
.
.
Ми довели теорему. Для
того щоб числа 0 знаходилось між коренями
рівняння
,
необхідно і достатньо, щоб виконувалася
умова
.
Розглянемо
задачу, що узагальнює одержаний результат.
З’ясуємо,
за
яких умов фіксоване число
знаходиться
між коренями рівняння
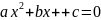 ,
тобто виконується умова
,
тобто виконується умова

З
умови випливає, що
 Нехай
Нехай
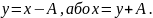 Тоді
Тоді
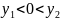 ,
де
,
де
 корені
рівняння
корені
рівняння
 або
або
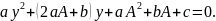 Як
було з’ясовано раніше, для виконання
умови
необхідно і достатньо, щоб виконувалася
умова
Як
було з’ясовано раніше, для виконання
умови
необхідно і достатньо, щоб виконувалася
умова