Таким образом, получаем окончательно (6) Проверка дает и

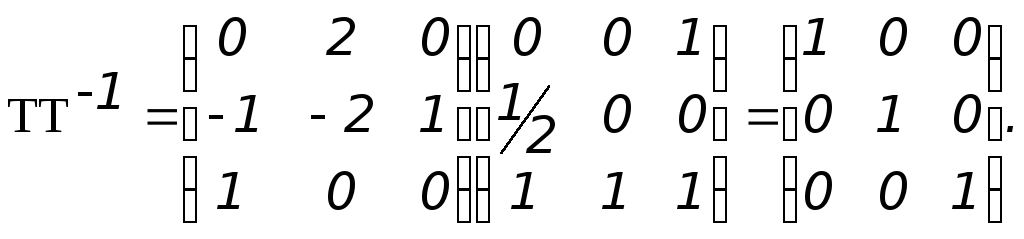
1.3. Построить невырожденную матрицу Т преобразования подобия другим методом (путем построения преобразующей матрицы по матрицам элементарных операций).

Этот метод состоит в следующем. Из подобия матриц A и J следует, что характеристические матрицы E - A и E - J эквивалентны, т.е. по теореме о связи между подобием и эквивалентностью имеет место тождество

E - J = P() (E-A) Q(), (7)

где P() и Q() - преобразующие -матрицы с постоянными, (независимыми от ) и отличными от нуля определителями. Воспользуемся следующим фактом из теории -матриц (следствие из доказательства теоремы о связи между подобием и эквивалентностью): если A и J - две подобные матрицы, т.е.

A = T J T ^-1 , (8)

или J = T ^-1 A T, то в качестве преобразующей матрицы Т можно взять правое Q^ПР.ЗН(J) или левое обратное [P^ЛЕВ.ЗН.(J)]^-1 матричные значения преобразующей матрицы, полученные при подстановке в них справа или слева матрицы J вместо скалярной переменной :

T = Q^{П Р.ЗН.}(J) = [P^ЛЕВ.ЗН.(J)]^-1 (9)

где Q() и P() - - матрицы из тождества (7).

Замечание 1. Важно обратить внимание на однозначную связь между видом соотношений (7), (8) и (9) с точки зрения местоположения матриц A и J. Так, если в (8) поменять местами матрицы A и J, то и в соотношениях (7) и (9) надо также переставить их местами.

Замечание 2. Разумеется, что в приведенном факте матрица J не обязательно должна быть жордановой формой, а может быть любой матрицей, подобной А.

Из изложенного вытекает следующая методика вычисления матрицы Т.

Шаг 1. Приведем к канонической диагональной форме ( обозначим ее как D()), каждую из -матриц E-A и E-J при помощи соответствующих левых и правых элементарных операций. Очевидно, что в силу эквивалентности E-A и E-J они приводятся к одной и той же диагональной форме:

diag (i₁()...i_n()) = D() = P₁()( Е-А)Q₁() = P₂()(E-J)Q₂() (10)

Шаг 2. Матрицы P₁(), P₂() и Q₁(),Q₂() вычислим, перемножая соответствующие левые и правые элементарные матрицы.

Шаг 3. Вычислим Q() или P(), приравнивая тождества (10) друг другу и приводя к тождеству вида (7) E-J= P₂^-1()P₁()(E-A)Q₁()Q₂^-1().

Таким образом, получим, что

Q()= Q₁()Q₂^-1(); P()= P₂^-1()P₁() (11)

Шаг 4. Подставим в матрицу Q() справа или в матрицу P() слева вместо переменной  матрицу J и получим матрицу Т по формуле (9).

Замечание 3. Достаточно рассчитать одну матрицу Q() = Q₁()Q₂^-1() и получить Т = Q^П(J). Ясно, что матрица Т при этом не будет равна числовой матрице Т, полученной в пункте 1.2 в виде (5), но она, конечно, будет удовлетворять соотношению подобия (8).

Проведем конкретные расчеты по изложенной методике. Мы уже преобразовали матрицу Е-А к диагональному виду в пункте 1.2. Запишем этот результат в виде (10):

diag{1;1;( -2)( -4)²}= P₁()( E-A)Q₁(). (12)

Вычислим Q₁() как произведение всех правых элементарных матриц, соответствующих правым элементарным операциям в (2). Но это равносильно тому, чтобы вычислить Q₁(), применяя последовательно к столбцам единичной матрицы Е эти правые элементарные операции:

,

Теперь приведем характеристическую матрицу E-J к каноническому диагональному виду, очевидно, тому же, что и (12): diag{1; 1; (-2) ( -4)²} = P₂() ( E-J) Q₂().

Легко проверить, что применяя к ней следующие элементарные операции:

(13)

получим каноническую диагональную форму для матрицы E-J, что и запишем в виде (10): diag{1,1,(-2)(-4)²}= P₂()( E-J)Q₂().

Вычислим Q₂(), применяя к столбцам единичной матрицы Е последовательно только правые элементарные операции из (13):

Итак, вычислили Q₁() и Q₂(). Заметим, что detQ₁() = -1/4, detQ₂() = 4, т.е. Q₁() и Q₂() удовлетворяет условиям теоремы о первом признаке эквивалентности.

Для того, чтобы рассчитать матрицу Q()=Q₁()Q₂^-1() надо обратить матрицу Q₂(). Чтобы избежать этой трудоемкой операции , поступим иначе.

Так как Q₂()=T₂T₃T₆T₇T₁₂T₁₃, где Т_i -правые элементарные матрицы правых операций из (18), то Q₂^-1()=T₁₃^-1T₁₂^-1T₇^-1T₆^-1T₃^-1T₂^-1.

Обращая эти операции, получим

Q₂^-1()=[3+(-4)²2][(1/4) 3],[2-(1)3], [2,1],[3,2],[2-(-4)3].

Тогда применяя эти обратные операции к единичной матрице Е, получим

Проверим правильность обращения Q₂(). Должно быть det [Q₂()Q₂^-1()] = = det Q₂() det Q₂^-1()= 4 1/4=1.

Проверим также , что выполняется равенство Q₂()Q₂^-1()=E ( самостоятельно).

Рассчитаем Q()=Q₁()Q₂^-1(),

Q()=

Заметим для проверки, что det Q() = det Q₁()det Q₂^-1() = -1/4 1/4 = -1/16. Перепишем Q() в форме матричного многочлена:

Вместо  подставим справа: . (14)

Легко проверить, что det T = т.е. матрица T – неособенная, а значит, обратная матрица T^-1 существует. Теперь, чтобы окончательно убедиться в правильности расчета Т, проверим выполнение равенства (8) А = ТJT^-1, записывая его в виде АТ = ТJ:

Вывод: Рассчитали преобразующую матрицу T вида (14) другим методом. Разумеется, в силу её неединственности получили другую числовую матрицу T, чем в пункте 1.2 в формуле (5), и проверим, что она удовлетворяет соотношению, записанному в виде (3). Отметим, что для такой проверки не надо вычислять обратную матрицу T^-1. Её вычисление необходимо только для выполнения следующего пункта.