10

Санкт-Петербургский государственный

электротехнический университет “ЛЭТИ”

Кафедра систем автоматического управления курсовая работа

по дисциплине

Математические основы теории систем

(4-й семестр)

Лектор: д.т.н. проф. Путов В.В.

Консультант: асп. Гайдым Д.А.

Выполнил: студент группы 7323

подпись Ф.И.О.

Проверил Гайдым Д.А.

с оценкой

Санкт-Петербург. 1999 г.

Задание 1. Для данной числовой матрицы

А= (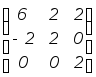1) с помощью элементарных операций привести её характеристическую матрицу (Е-А) к каноническому диагональному виду, определить элементарные делители и построить нормальную жорданову форму J. Рассчитать матрицу преобразования Т и вычислить экспоненциалы матриц F и J с параметром (t-t₀).

1.1 Построить нормальную жорданову форму заданной числовой матрицы.

Для этого введем следующие символические обозначения для левых (S) и правых (T) элементарных операций и соответствующих им матриц

S^I={(c) i}; S^II={i+(b()) j}; S^III={ij}; T^I=[(c) i] T^II=[i+b()) j], T^III=[ij],

где S^I( T^I) - первая левая (правая) элементарная операция умножения i-ой строки (i-го столбца) на число C0; S^II( T^II) - вторая левая (правая) элементарная операция прибавления к i-ой строке ( i-ому столбцу) другой j-ой строки ( j-го столбца), предварительно умноженной ( умноженного) на произвольный многочлен b(); S^II( T^II) - третья левая ( правая) элементарная операция перестановки местами i-ой строки ( i-го столбцу) и j-ой строки ( j-го столбца).

Характеристическая -матрица имеет вид Е -А =.

Следуя методике диагонализации -матрицы, описанной в теореме о существовании канонической диагональной формы -матрицы, выполним последовательно над матрицей (1) следующие элементарные операции:

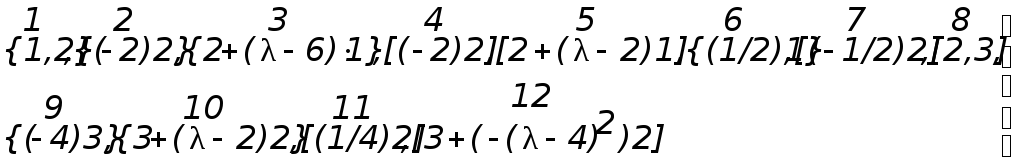(2)

пронумерованные цифрами 1, ... ,12, стоящими над обозначениями операций.

Легко проверить ,что с помощью этих элементарных операций матрица (1) приводится к канонической диагональной форме:

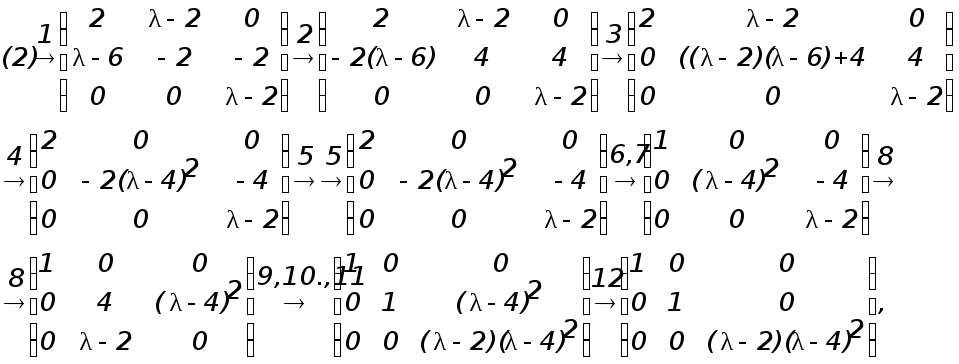
где над стрелками указаны порядковые номера элементарных операций.

Из канонического диагонального вида характеристической матрицы (1) видно, что эта матрица имеет инвариантные множители вида:

где - минимальный многочлен матрицы А. Следовательно, имеется два элементарных делителя (-2) и (-4)². Поэтому исходная матрица А вида (1) имеет следующую жорданову форму J=.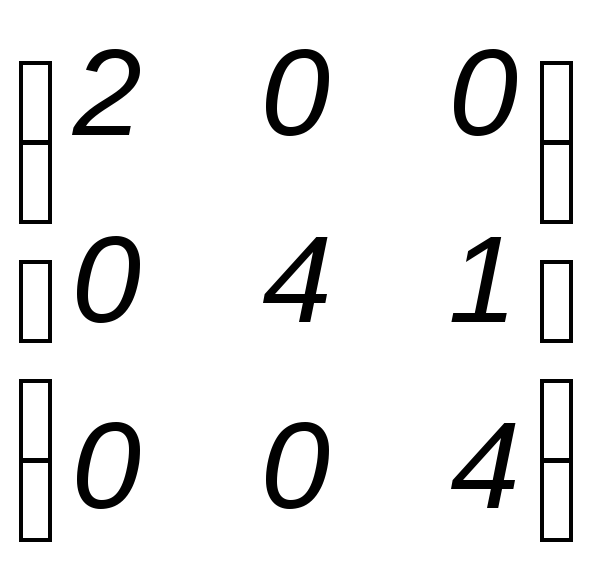

1.2. Построить невырожденную матрицу Т преобразования подобия методом прямого решения матричного уравнения.

Преобразование подобия имеет вид , где Т - числовая невырожденная матрица. Непосредственно решаем матричное уравнение

АТ - ТJ=0. (3)

Уравнение (3) имеет множество решений Т, поэтому нужно наложить дополнительное условие det T 0.

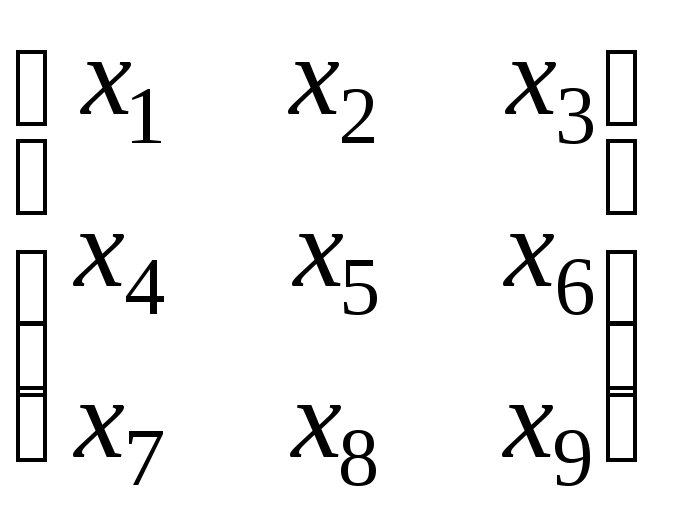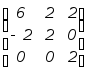
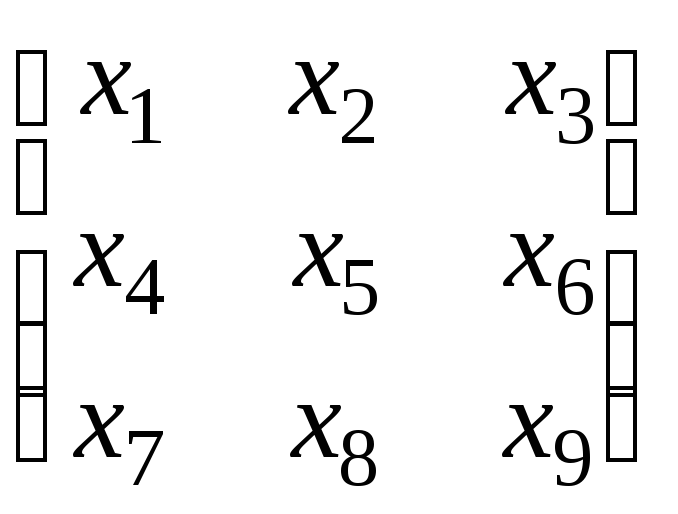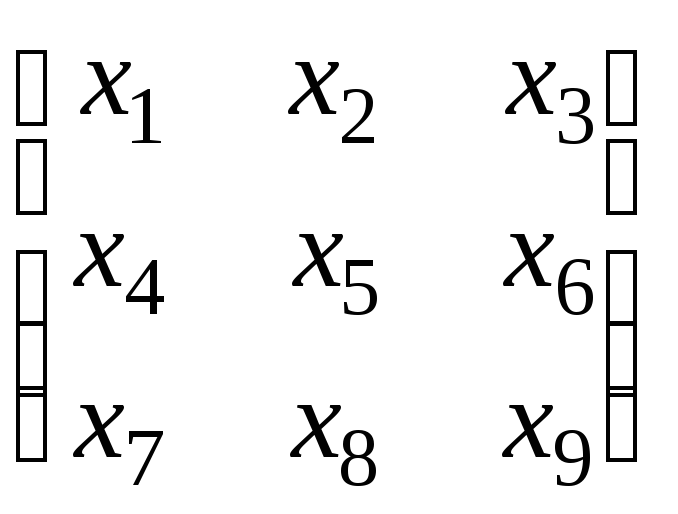
Обозначая элементы матрицы Т=, раскроем матричное уравнение (3) =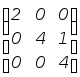. (3’)

Выполняя действия над матрицами, запишем 9 скалярных уравнений:

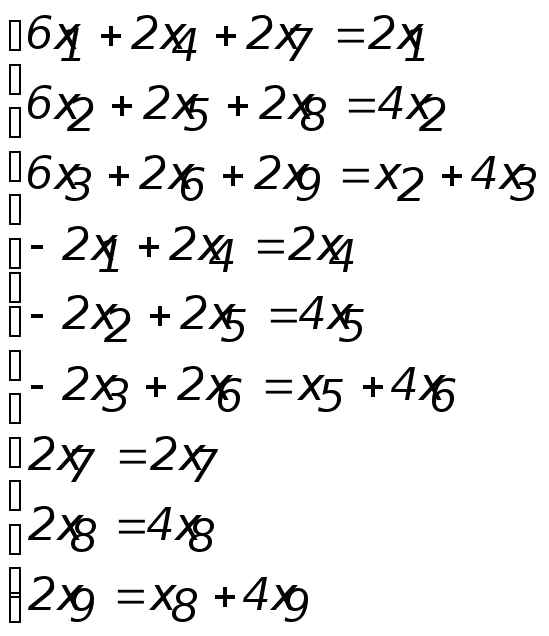(4)

Из 4-го уравнения системы (4) будет х₁=0; Из 8-го и 9-го уравнения х₈ = 0, х₉ = 0.

Получили матрицу Т=.

Из 7-го уравнения системы (4) х₇ можно принять любым, но из условия det T 0 элемент х₇ не может быть равен нулю, поэтому примем х₇=1, тогда х₄ = - х₇ = -1.

Получили

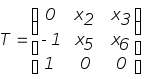
Оставшиеся уравнения системы (4) -x + x₅ = 2x₅  x₂ + x₅ = 0 ; 2( x₃ + x₆) = x₂

решаем с дополнительным условием, чтобы

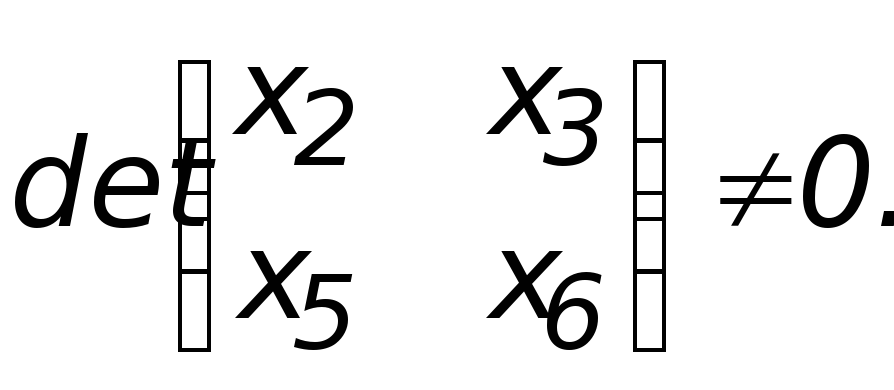
Пусть x₃ = 0, тогда x₆ = 1, и пусть x₂ = 2, тогда x₅ = -2.

Окончательно получим

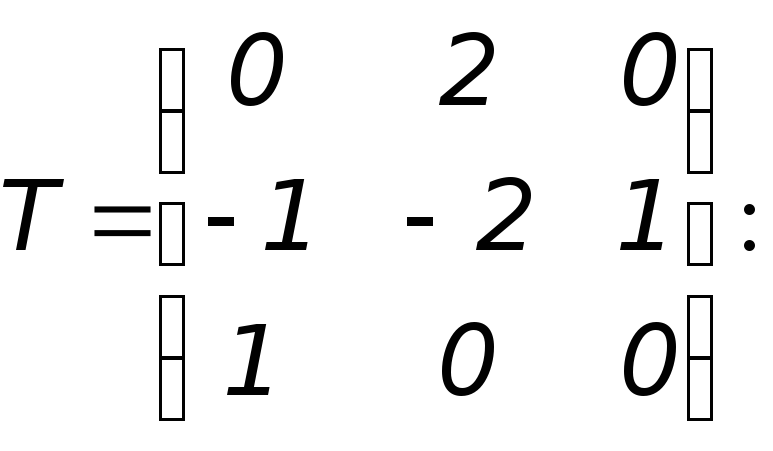det T = 2  0 (5)

Для проверки подставим матрицу (5) в уравнение (3). Получим

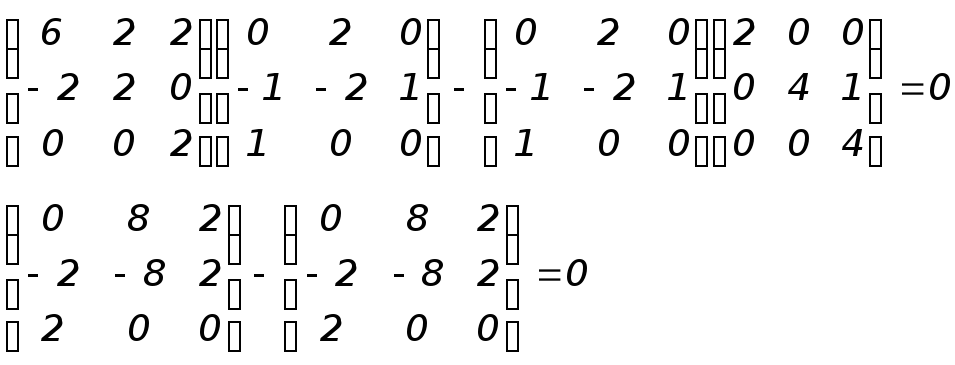
Проверили, что матрица Т удовлетворяет уравнению (3) и, следовательно, рассчитана правильно.

Вычислим матрицу Т^-1 по формуле Т^-1 = ,где Т^* - присоединенная матрица к матрице Т, т.е. матрица, составленная из алгебраических дополнений к элементам матрицы Т и транспонированная. Пусть Т = {t_ij}, i,j = 1,2,3. Алгебраическим дополнением для t_ij будет A_ij = (-1)^i+jM_ij, где M_ij - ij-й минор матрицы Т есть определитель числовой матрицы, составленной из оставшихся элементов матрицы Т после вычеркивания ее i -ой строки и j -го столбца.

Вычисляя, получим