Оверлей полігонів
Прості алгоритми, розглянуті раніше, формують базис для більш складних алгоритмів ГІС-аналізу, таких, як оверлеї полігонів. Ця операція традиційно використовується в ландшафтному плануванні, де з метою управління використання земель досліджуються просторові взаємозв'язки між накладеними один на одного географічними шарами.
Оверлеї полігонів ізоморфні операціям теорії множин. Коли накладаються два полігони A і B, виходить графічна інтерпретація об'єднання або перетину множин A і B. На рис. 4.8 показані шістнадцять можливих оверлейних операцій з двома полігонами, виражені через об'єднання, перетин і заперечення помічених цифрами 1 ... 4 множин.
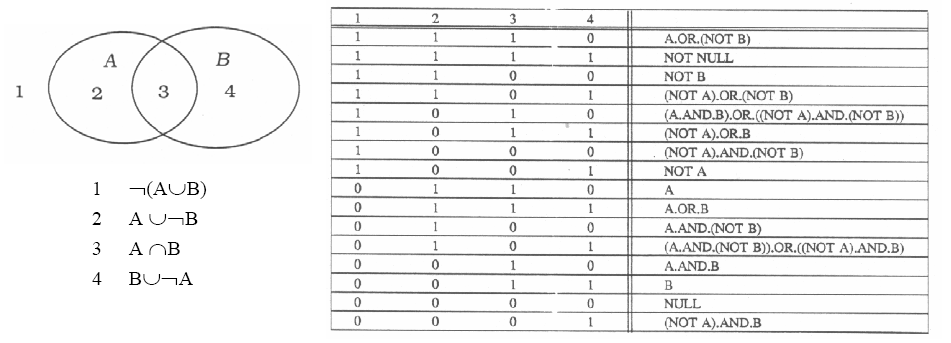
Рисунок 4.8 – Зв'язок оверлеїв полігонів з операціями теорії множин.
На основі оверлейних операцій будуються деякі інші функції ГІС. При візуалізації даних інтерес представляють тільки об'єкти, які потрапляють у "вікно" користувача, а інші об'єкти для прискорення відображення повинні бути пропущені. Для цього на шари карти накладається прямокутник – екстент карти, поза яким об'єкти не відображаються. При побудові буферів навколо точок, сегментів поліліній і полігонів створюються кола та прямокутники, які згодом оверлейною операцією зливаються в один об'єкт.
Оверлейні операції застосовуються при площинній інтерполяції. Тут потрібно розподілити деяку величину, пов'язану з полігоном A, між перетином A ∩ B і різницею A – B пропорційно їх площі. При цьому вважається, що щільність цієї величини по всьому полігону постійна.
Перейдемо тепер до способів реалізації оверлейних операцій. Будемо розглядати найбільш поширений в ГІС-аналізі випадок, коли накладаються два шари з непересічними полігонами. Уявімо, що в одному з шарів містяться "червоні" полігони, а в іншому – "сині". Тоді завдання полягає в пошуку полігонів на комбінованому "фіолетовому" шарі. Атрибути цього шару містять характеристики "синіх" і "червоних" полігонів. Кількість полігонів, одержаних в результаті накладення шарів, заздалегідь передбачити не можливо. З перетинання "синього" і "червоного" полігонів може вийти як завгодно багато "фіолетових".
Щоб отримати оверлей двох полігонів, спочатку необхідно обчислити всі перетини між їх границями. На рис. 4.9 зображений "червоний" полігон з атрибутом "A" (тонкі лінії) і синій полігон з атрибутом "1" (товсті лінії). Зовнішня частина на обох картах має атрибут "0". Кожен полігон представлений однією дугою, для кожної з них відомо, з якого боку розташований полігон. Після обчислення перетинів цих дуг утворюються шість нових дуг і чотири нових полігонів, що наслідують атрибути 00, A0, A1, 01. Для нових дуг також відомо, які полігони лежать праворуч і ліворуч.
По таблиці суміжності одержаних дуг і полігонів можна сформувати будь-який з можливих шістнадцяти полігонів, показаних на рис. 4.8.
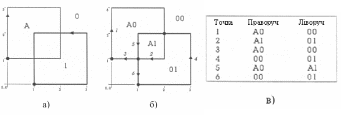
Рисунок 4.9 – Оверлей полігонів в моделі "дуга-вузол": а) вихідні об'єкти;
б) обчислення перетинів дуг; в) мітки суміжності дуг і полігонів
Розглянемо більш складний приклад (рис. 4.10). Тут накладаються шар з об'єктом "1" і шар з трьома об'єктами "A", "B" і "C". Обчислимо перетин дуг об'єктів і отримаємо мітки правих і лівих полігонів нових дуг. Як видно з рисунка, дуги 3, 6 і 8 не мають перетинів з об'єктом "1". Визначимо мітки для третьої дуги. Зрозуміло, що мітки всередині полігону можуть передаватися від дуги до дуги. Правий полігон третьої дуги той же, що і праві полігони другої та четвертої дуги – "А1". Лівий полігон шостої дуги той же, що і ліві полігони другої та четвертої дуги – "А1". Для третьої дуги, як для частини мережі "червоного" шару, відома "червона" частина мітки лівого полігону – це "B". "Синя" частину лівої мітки береться з мітки правого полігону. У результаті виходить мітка "B1". Аналогічно, мітка правого полігону для шостої дуги буде "B1".
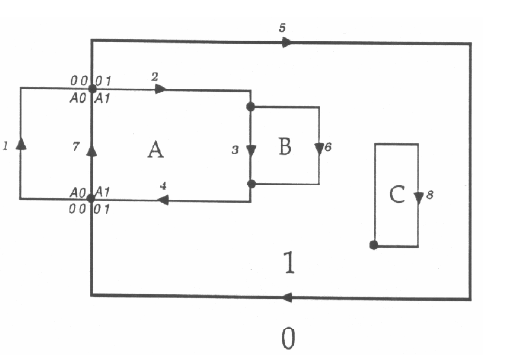
Рисунок 4.10 – Оверлей полігонів з непересічними границями
Восьма дуга не перетинається з межею полігона "1" і не є суміжною з іншими дугами границі "червоного" шару. Для ізольованої дуги за допомогою алгоритму "точка в полігоні" слід визначити вміст полігону "синього" шару. Отримаємо для восьмої дуги правий полігон "С1" і лівий полігон "01". Останній крок оверлейного алгоритму полягає у формуванні полігонів з нових дуг шляхом обходу полігону від дуги до дуги до тих пір, поки полігон не замкнеться. Точність подання координат сегментів в машинній формі більш висока, ніж похибки оцифрування і векторизації. Тому при пошуку перетинань сегментів полігону можуть виникати помилки, пов'язані з відсутністю відомостей про топологічну структурі об'єктів. На рис. 4.11-а і на рис. 4.11-б показані два різних випадки перетину ліній.
З рисунків видно, що в першому випадку лінії перетинаються насправді, а в другому випадку пересічні ділянки ліній представляють одну і ту ж границю. Необхідно складати оверлейні алгоритми таким чином, щоб розрізняти ці ситуації. Полігони, які утворюються при оверлеї двох полігонів з помилково векторизованими спільними кордонами, називаються розщепленими. Розщеплені полігони можуть бути усунуті або в процесі оверлейної операції, або після її виконання.
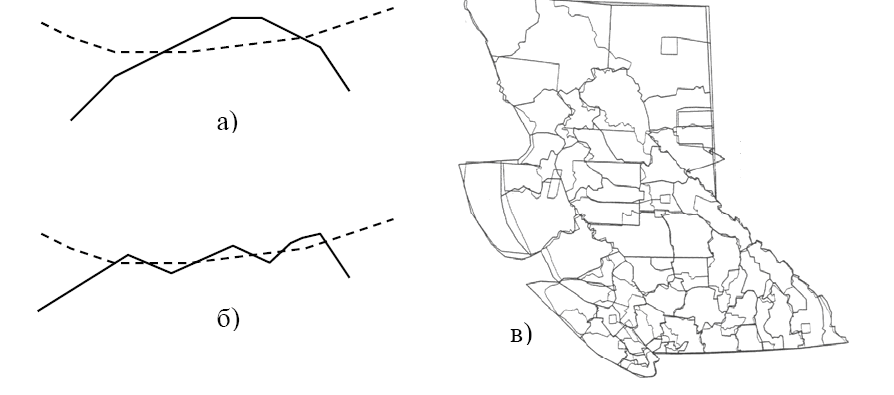
Рисунок 4.11 – Проблеми пошуку перетину полігонів: а) пересічні сегменти; б) помилкові перетини сегментів суміжних полігонів; в) розщеплені полігони
У більшості комерційних ГІС використовується перший підхід, що полягає в "нечіткому" поданні ліній. При цьому для кожної лінії задається рівень толерантності, пов'язаний з виникненням, через помилки векторизациї, невизначеністю геометрії лінії. Пошук перетинань ведеться для "смуг", заданих самою лінією і рівнем толерантності (рис. 4.12-а). Слід зауважити, що визначення перетинів для нечітких ліній не є транзитивним.
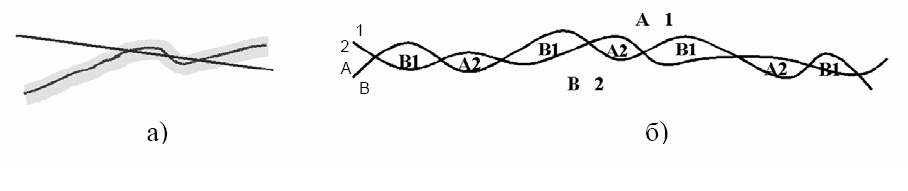
Рисунок 4.12 – Видалення розщеплених полігонів: а) до оверлейної операції; б) після оверлейної операції
Для усунення розщеплених полігонів після оверлейної операції необхідно визначити критерії, за якими розщеплений полігон можна відрізнити від справжнього. Розщеплені полігони зазвичай мають невелику площу і витягнуту форму. Вони найчастіше складаються з двох дуг. Розщеплені полігони характеризуються також "переміжними" атрибутами. Якщо синя дуга з атрибутами "1" і "2" накладається на "червону" дугу з атрибутами "A" і "B", розщеплені полігони будуть мати атрибути "B1" і "A2" (рис. 4.12, б).