Теория

1 Вероятность события. Классическое и статистическое определение вероятности. Основные теоремы теории вероятности

1.1 Вероятность события

Случайное событие — факт, который в результате опыта может либо произойти, либо не произойти.

Вероятность события — количественная мера степени его объективной возможности.

Достоверным называется событие, которое в результате опыта заведомо произойдет.

Невозможным называется событие, которое в результате опыта заведомо не произойдет.

Вероятность любого события есть число от 0 до 1!!!!

1.2 Классическое и статистическое определение вероятности

Классическое: вероятность события равна отношению количества благоприятных этому событию исходов к общему числу всех несовместных равновозможных исходов опыта, образующих полную группу.

Два события называются несовместными, если они не могут одновременно произойти в одном опыте.

Несколько событий называются равновозможными, если нет оснований считать какое-либо из них более возможным, чем другое.

Несколько событий образуют полную группу, если в результате опыта одно из них обязательно произойдет.

При подсчете значений n и m целесообразно пользоваться формулами комбинаторики:

а) число перестановок из k элементов:

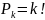
б) число размещений из k элементов по l:

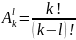
в) число сочетаний из k элементов l (порядок следования элементов не существенен):

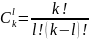
Статистическая вероятность события (частота) в данной серии опытов равна отношению количества опытов, в которых событие А появилось к общему количеству опытов.

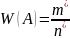
Статистическая вероятность справедлива только для данной серии опытов.

Если n^*→∞, то W(A)→P(A).

1.3 Основные теоремы теории вероятности

Сумма и произведение двух событий. Суммой двух событий А и В называется событие С, которое состоит в появлении либо А, либо В, либо А и В одновременно («ИЛИ»).

Сумма нескольких событий А_і, і=1,2,..,n состоит в появлении хотя бы одного из А_і.

Произведением двух событий А и В называется событие С, состоящее в одновременном появлении А и В («И»).

Произведение нескольких событий А_і, і=1,2,..,n состоит в совместном появлении всех этих событий.

Противоположными называются два несовместных события, образующих полную группу.

Теорема сложения вероятностей. Вероятность суммы двух НЕсовместных событий равна сумме их вероятностей

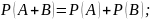
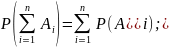
Вероятность суммы двух совместных событий равна сумме их вероятностей минус вероятность их совместного появления.

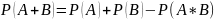
Теорема умножения вероятностей. Вероятность произведения двух НЕзависимых событий равна произведению их вероятностей.

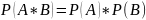
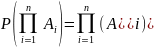
Вероятность произведения двух зависимых событий равна вероятности первого события на условную вероятность второго события.

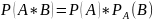
Два события А и В называются независимыми, если вероятность каждого из них не зависит от того, произошло другое событие или нет.

Событие В называется зависимым от события А, если его вероятность зависит от появления события А.

Вероятность появления хотя бы одного события. Вероятность появления хотя бы одного события А_і, і=1,2,..,n равна разности между единицей и вероятностью произведения противоположных событий 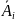, і=1,2,..,n.

2 Случайные величины и способы их задания. Числовые характеристики случайных величин и из свойства

2.1 Случайные величины и способы их задания

Случайной называется такая величина, которая в результате опыта принимает единственное значение, заранее неизвестно, какое.

Дискретной называется СВ, которая принимает дискретные значения с определенной вероятностью их появления.

Непрерывной называется СВ, которая принимает любое значение из некоторого конечного или бесконечного промежутка.

Закон распределения вероятностей дискретной СВ — соответствие между всеми возможными значениями СВ и вероятностями, с которыми эти значения наблюдаются.

Способы задания дискретных СВ:

1) табличный;

2) графический;

3) аналитический .

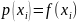2.2 Числовые характеристики св и их свойства

1) Математическое ожидание дискретной СВ — сумма произведений всех ее возможных значений на их вероятности.

Математическое ожидание характеризует среднее значение величины.

Свойства математического ожидания:

а) математическое ожидание постоянной равно самой постоянной;

б) постоянный множитель можно выносить за знак мат. ожидания;

в) мат. ожидание произведения двух независимых СВ равно их произведению;

г) мат. ожидание суммы двух СВ равно сумме их мат. ожиданий.

2) Дисперсия дискретной СВ — мат. ожидание квадрата отклонения СВ от ее мат. ожидания.

эта характеристика является квадратичной и характеризует отклонение дискретной СВ как выше мат. ожидания, так и ниже.

Дисперсия равна разности мат. ожидания квадрата и квадрата мат. ожидания.

Свойства дисперсии:

1) дисперсия постоянной равна самой постоянной;

2) постоянный множитель выносится за знак дисперсии, возведенный в квадрат;

3) дисперсия суммы независимых СВ равна сумме их дисперсий;

4) дисперсия разности независимых СВ равна сумме их дисперсий.

3) Среднее квадратическое отклонение равно корню квадратному из дисперсии.

4) Начальный момент порядка k — мат. ожидание СВ Х^k.

5) Центральным моментом порядка k наз. мат. ожидание СВ (Х-М(Х))^k.