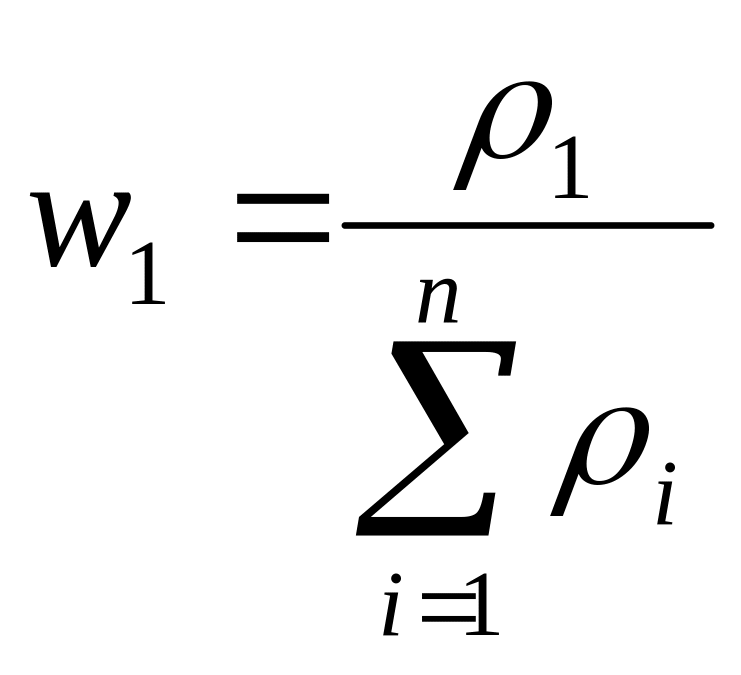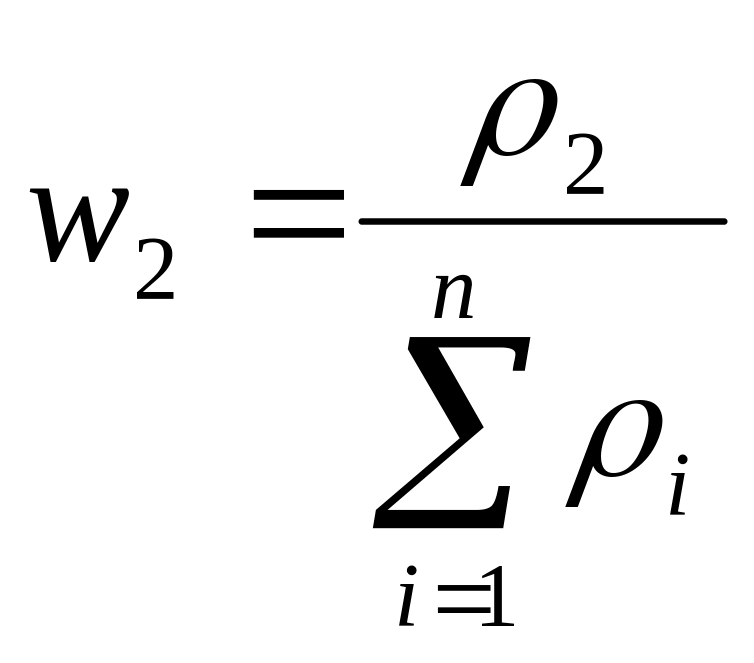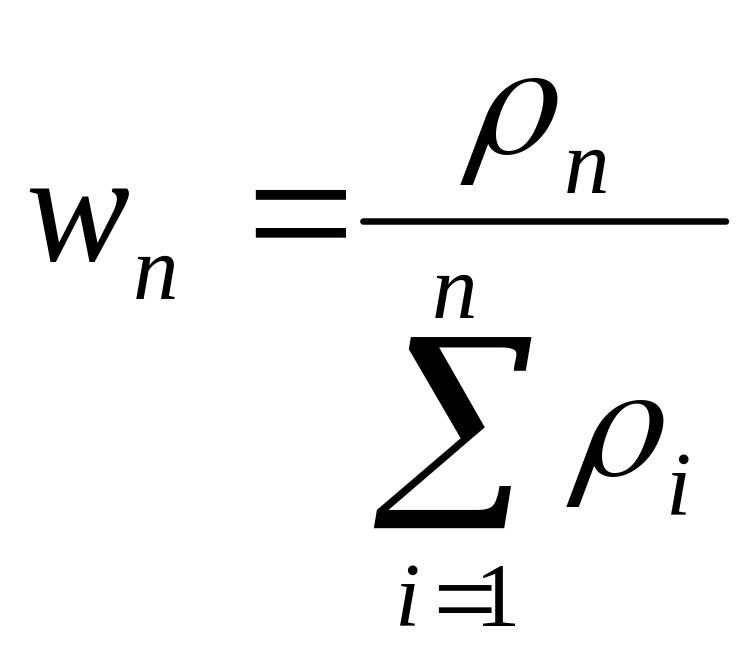2.2. Применение метода анализа иерархий при отборе кадров

Сущность метода анализа иерархий (МАИ), который был предложен американским ученым Т. Саати, заключается в декомпозиции сложной проблемы путем построения иерархии (главная цель разбивается на подчиненные ей задачи, которые в свою очередь разбиваются на более простые подзадачи и так далее). В МАИ проблема субъективизма разрешается за счет применения шкалы попарных сравнений, которую разработал Т. Саати.

Построение иерархической структуры цели «Отбор кандидата на должность» (рис. 1) предлагается осуществлять так:

• на вершине иерархии изображается главная цель (в нашем случае это – отбор кандидата на должность);

• для каждой должности в организации разрабатывается перечень требований или критериев (второй иерархический уровень): уровень образования, общий и специальный опыт работы, владения иностранными языками, личные характеристики и т.д.; наличие, и степень проявления этих критериев у кандидатов оценивается экспертами, осуществляющими отбор;

• нижний уровень иерархии формируют возможные претенденты на замещение вакансии, то есть альтернативные варианты достижения главной цели.

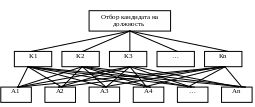
Рис. 1. Иерархическая структура цели «Отбор кандидата на должность»

Следующий шаг в реализации МАИ – построение множественного числа попарных сравнений для каждого иерархического уровня. Оценки во время сравнения отдельных элементов выставляются, исходя из следующей шкалы (табл.1).

Таблица 1

Шкала попарных сравнений, предложенных Т. Саати

Степень важности	Определение	Объяснение
1	Одинаковая значимость	Альтернативы одинаковы с точки зрения достижения цели
3	Слабая значимость	Опыт и суждения дают легкое преимущество одной альтернативе над другой
5	Существенная или сильная значимость	Опыт и суждения дают сильное преимущество одной альтернативе над другой
7	Очень сильная или очевидная значимость	Преимущество одной альтернативы над другой становится практически явным
9	Абсолютная значимость	Преимущество одной альтернативы над другой становится очевидным и подтверждается в большинстве случаев
2,4,6,8	Промежуточные значения между соседними значениями шкалы	Ситуации, которые требуют компромиссных решений
Обратные значения чисел	Если альтернативе і во время сравнения с альтернативой j дается одна из оценок приведенных выше, то альтернативе j во время сравнения с альтернативой і дается обратная оценка

В первую очередь строится матрица С попарных преимуществ для перечня критериев (табл. 2).

Таблица 2

Общая структура матрицы попарных сравнений критериев

			…		Собственный вектор ( )	Нормированный вектор или весовые коэффициенты ( )
	1	с12	…	с1n
		1	…	с2n
…	…	…	1	…	…	…
			…	1
						1

Таким образом, матрица С имеет следующий вид:

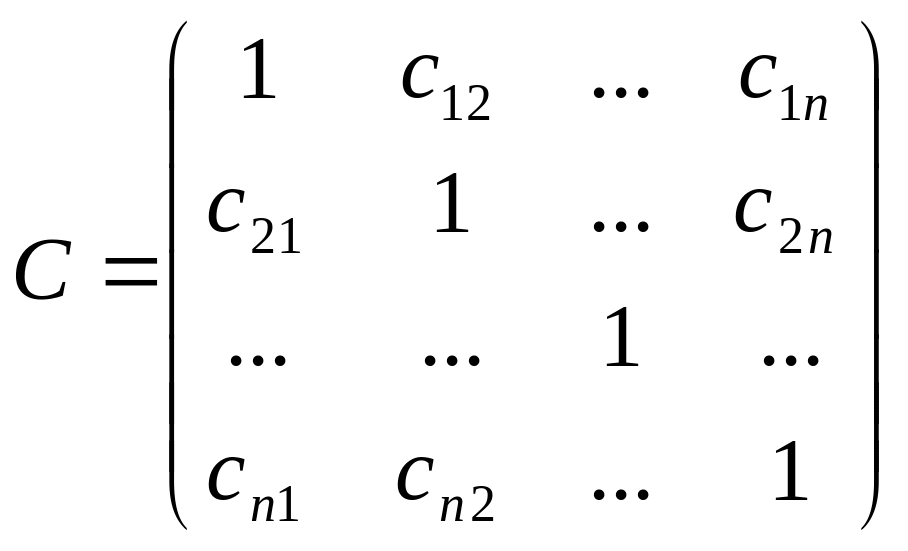
Матрица строится по следующим правилам. Она является квадратной, размерность матрицы С соответствует количеству критериев – n. Если і-й критерий важнее j-го, то при помощи шкалы из табл. 1 ему присваивается соответствующая балльная оценка (элементу присваивается соответствующее значение в баллах, а элементу - обратное значение ). То есть, матрица С является обратно симметрической, для всех элементов выполняется равенство , а элементы главной диагонали равняются 1.

Для элементов матрицы рассчитывается собственный вектор ( ) и нормированный вектор ( ) по формулам, которые изображены в таблице 2. Отдельные элементы нормированного вектора являются весовыми коэффициентами ( ), то есть отображают значимость каждого из элементов.

По тем же правилам строится матрица альтернатив А. Определяются весовые коэффициенты альтернатив ( ).

Принятие окончательного решения базируется на расчете значения вектора глобальных приоритетов, который определяется как произведение соответствующих весовых коэффициентов:

(1)

Номер максимального значения вектора глобальных приоритетов соответствует порядковому номеру победителя отбора.

Задание: определить наиболее подходящего претендента в заданных условиях.

В качестве критериев отбора претендентов были выбраны следующие:

1. уровень образования;

2. стаж работы;

3. возраст;

4. результаты профессионального тестирования;

5. общее впечатление о претенденте по итогам собеседования (включает такие параметры, как коммуникабельность, мотивационные установки, эмоциональный интеллект и т.д.).

Руководством предприятия было проведено попарное сравнение критериев и было определено:

1. Стаж работы существенно значимее, чем уровень образования;

2. Возраст чуть значимее, чем уровень образования;

3. Результаты профессионального тестирования существенно значимее, чем уровень образования;

4. Общее впечатление существенно значимее, чем уровень образования;

5. Стаж работы чуть значимее, чем возраст;

6. Стаж работы чуть значимее, чем результаты профессионального тестирования;

7. Общее впечатление существенно значимее, чем стаж работы;

8. Результаты профессионального тестирования чуть значимее, чем возраст;

9. Общее впечатление значительно значимее, чем возраст;

10. Общее впечатление чуть значимее, чем результаты профессионального тестирования.

На замещение вакансии претендуют следующие кандидаты:

Кандидат А:

• специалист в данной сфере с отличием;

• стаж работы – 3 года;***

• возраст – 39 лет;

• результаты проф. тестирования – 86%.

Кандидат Б:

• магистр;

• стаж работы – до 1 года;

• возраст – 37 лет;

• результаты проф. тестирования – 96%.

Кандидат В:

• магистр в данной сфере;

• стаж работы – 2 года;

• возраст – 24 лет;

• результаты проф. тестирования – 46%.

Кандидат Г:

• специалист с отличием;

• стаж работы – 4 года;

• возраст – 28 лет;

• результаты проф. тестирования – 76%.

*** - в случае если отсутствуют комментарии, то опыт работы в данной сфере

Общее впечатление о претендентах:

1. А чуть лучше, чем Б;

2. В существенно лучше, чем А;

3. Г значительно лучше, чем А;

4. Б чуть лучше, чем В;

5. Г абсолютно лучше, чем Б;

6. Г существенно лучше, чем В.

Значения критериев переводятся в баллы на основании следующей информации (табл. 3).

Таблица 3

Соответствие баллов и значений критериев отбора

Критерий	Баллы и значение критериев отбора
	1	2	3	4	5	6	7	8	9
Уровень образования	Бакалавр	Специалист	Магистр	Специалист с отличием	Магистр с отличием	Специалист в данной сфере	Магистр в данной сфере	Специалист в данной сфере с отличием	Магистр в данной сфере с отличием
Стаж работы	0	до 1 г. в другой сфере	более 1 г. в другой сфере	до 1 года	от 1 года до 3х включительно	от 3х лет до 5 включительно	от 5 лет до 7 включительно	от 7 лет до 10 включительно	более 10 лет
Возраст (лет)	18-22; 43-45	23; 42	24; 41	25; 40	26; 39	27; 38	28; 37	29; 36	30-35
Результаты проф. тестирования (%)	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
Общее впечатление о претенденте	Проводится попарное сравнение в соответствии со шкалой Саати

На основании имеющейся информации строится матрица попарных сравнений критериев.

Таблица 4

Структура матрицы попарных сравнений критериев

	Уровень образования	Стаж работы	Возраст	Результаты профессионального тестирования	Общее впечатление о претенденте
Уровень образования	1	1/5	1/3	1/5	1/5
Стаж работы	5	1	3	3	1/5
Возраст	3	1/3	1	1/3	1/7
Результаты профессионального тестирования	5	1/3	3	1	1/3
Общее впечатление о претенденте	5	5	7	3	1

Тогда, матрица будет иметь вид:

Для каждой строки матрицы рассчитываем значение собственного вектора и весовые коэффициенты каждого из критериев.

Таблица 5

Расчет собственных и нормированных векторов для критериев отбора

Критерии	Собственный вектор ( )	Нормированный вектор или весовые коэффициенты ( )
Уровень образования
Стаж работы
Возраст
Результаты профессионального тестирования
Общее впечатление о претенденте
		1

Таким образом, нами получен нормированный вектор для перечня критериев отбора со следующими координатами (координаты нормированного вектора являются весовыми коэффициентами соответствующих критериев):

Таблица 6 заполняется на основании информации, представленной в таблице 3 (значения критериев переводятся в баллы).

Таблица 6

Балльная оценка степени проявления критериев у кандидатов

	Образование	Стаж работы	Возраст	Результаты проф. тестирования
А	8	5	5	8
Б	3	4	7	9
В	7	5	3	4
Г	4	6	7	7

То есть, если мы сравниваем кандидата Б с кандидатом Г по критерию «стаж работы», получим 4/6, а кандидата Г с кандидатом Б 6/4 и т.д.

Теперь проведем попарное сравнение кандидатов по каждому из критериев.

1. Уровень образования:

	А	Б	В	Г	Собственный вектор ( )	Нормированный вектор ( )
А	1	8/3	8/7	2
Б	3/8	1	3/7	3/4
В	7/8	7/3	1	7/4
Г	1/2	4/3	4/7	1

2. Стаж работы:

	А	Б	В	Г	Собственный вектор ( )	Нормированный вектор ( )
А	1	5/4	1	5/6
Б	4/5	1	4/5	4/6
В	1	5/4	1	5/6
Г	6/5	6/4	6/5	1

3. Возраст

	А	Б	В	Г	Собственный вектор ( )	Нормированный вектор ( )
А	1	5/7	5/3	5/7
Б	7/5	1	7/3	1
В	3/5	3/7	1	3/7
Г	7/5	1	7/3	1

4. Результаты профессионального тестирования:

	А	Б	В	Г	Собственный вектор ( )	Нормированный вектор ( )
А	1	8/9	2	8/7
Б	9/8	1	9/4	9/7
В	1/2	4/9	1	4/7
Г	7/8	7/9	7/4	1

5. Общее впечатление

	А	Б	В	Г	Собственный вектор ( )	Нормированный вектор ( )
А	1	3	1/5	1/7
Б	1/3	1	3	1/9
В	5	1/3	1	1/5
Г	7	9	5	1

Таким образом, матрица нормированных векторов для различных критериев и кандидатов имеет вид:

Вектор глобальных приоритетов находится по формуле 1 и представляет собой произведение весовых коэффициентов каждого из критериев:

Так как максимальное значение у элемента с порядковым номером 4, то кандидат Г является наилучшим в данных условиях.

Решение задачи отбора оптимального кандидата при помощи MS Excel

Для расчета значения собственного вектора целесообразно пользоваться функцией ПРОИЗВЕД, а извлечение корня n-й степени соответствует возведению в степень 1/n. Тогда, например, функция корня 4-й степени из произведения чисел имеет вид:

=(ПРОИЗВЕД(ЧИСЛО1:ЧИСЛО2))^(1/4)

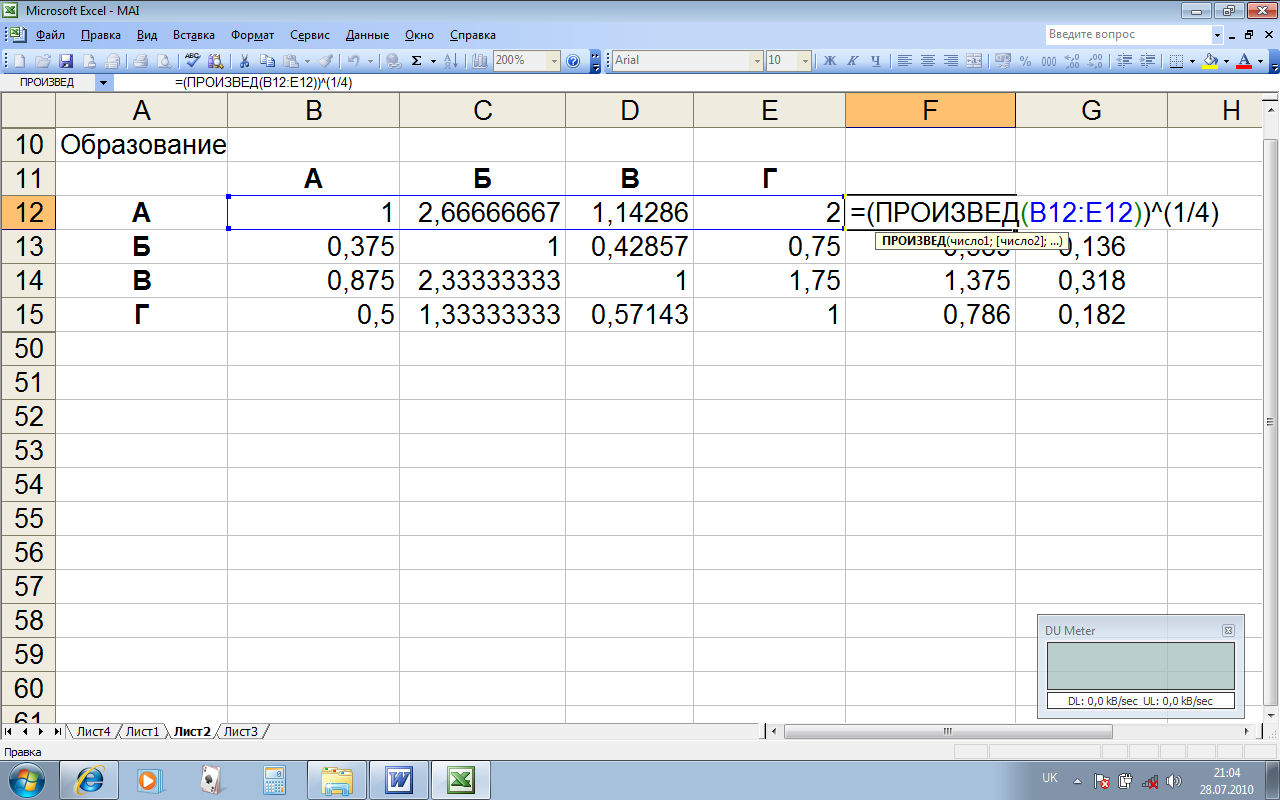
Перемножение матриц.

1. Требование: количество столбцов матрицы 1 должно быть таким же, как количество сток матрицы 2, и оба массива должны содержать только числа.

2. Функция перемножения матриц МУМНОЖ.

3. В качестве Массива 1 вводятся данные матрицы 1, в качестве массива 2 значения матрицы 2.

4. Выделяется диапазон размерностью соответствующей матрице произведения (число строк, как матрица 1 и с таким же числом столбцов, как матрица 2).

5. Нажимается клавиша F2, затем сочетание клавиш CTRL+SHIFT+ENTER.