1.5.14.3. Формула конечных приращений (теорема Лагранжа)

Теорема. Если функция определена и непрерывна на [a,b] и дифференцируема на (a,b), то внутри сегмента [a,b] найдется точка  такая, что справедлива формула f(b)-f(a)= (b-a).

(Формула f(b)-f(a)= (b-a) называется формулой Лагранжа или формулой конечных приращений).

Доказательство. Рассмотрим на сегменте [a,b] вспомогательную функцию (рис.1)

.

Проверим, что для функции F(x) выполнены все условия теоремы Ролля.

1) F(x)C[a,b] (как разность f(x) и линейной функции);

2)  ;

3) F(a)=F(b)=0.

По теореме Ролля , т.е.

.

Теорема доказана.

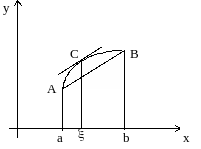
Рис. 1

Замечание 1. Напишем уравнение прямой l, проходящей через точки A(a, f(a)) и B(b,f(b)).

.

Отсюда .

Вычитая эту функцию из f(x), получим F(x), для которой F(a)=F(b)=0.

Угловой коэффициент построенной прямой l равен . Теорема Лагранжа утверждает, что найдется такая точка (a,b), в которой угловой коэффициент касательной совпадает с угловым коэффициентом прямой l, т.е. касательная к графику функции в точке С(,f()) параллельна прямой l, проходящей через точки A и В.

Замечание 2. Другой вид формулы Лагранжа.

Пусть х₀ -любое значение аргумента из [a,b], а х- произвольное приращение аргумента, но такое, что Тогда формула Лагранжа для сегмента [x₀ ,x₀+ х] имеет следующий вид: , где - некоторая точка из интервала

(x₀ ,x₀+ х) (см. рис.2).

Рис. 2

Можно утверждать, что найдется такое число  (0<<1), зависящее от х, что = x₀+ х, тогда , где некоторое число: 0<<1.

Этот вид формулы оправдывает термин “формула конечных приращений”, ибо дается выражение для приращения функции через вызвавшее его произвольное конечное приращение х аргумента.

Следствие 1.

Доказательство. Пусть x₀ (a,b)- фиксированна, x (a,b)- произвольная точка. На [x₀, x] (и [x, x₀] соответственно) f(x) дифференцируема. Применим теорему Лагранжа на этом сегменте: Но

1.5.14.4. Обобщенная формула конечных приращений (формула Коши).

Теорема. (теорема Коши)

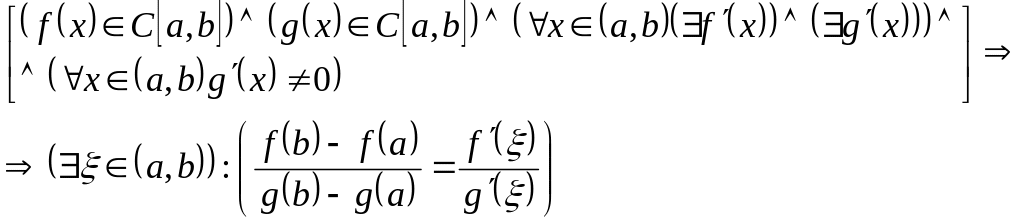
(Формула называется обобщенной формулой конечных приращений (формулой Коши)).

Доказательство.

1) Докажем, что g(a)g(b). Предположим, что g(a)= g(b), тогда к функции y=g(x) применима теорема Ролля на сегменте [a,b], по этой теореме

. Противоречие с условием теоремы Таким образом, g(a)g(b).

2) Рассмотрим вспомогательную функцию

Для функции F(x) выполнены на сегменте [a,b] все условия теоремы Ролля, действительно:

1)

2)

3)

По этой теореме

Теорема доказана.

Замечание. Формула Лагранжа является частным случаем формулы Коши для g(x)=x . (Теорема Ролля является частным случаем теоремы Лагранжа лишь формально, так как доказательство теоремы Лагранжа основано на теореме Ролля).

1.5.14.5. Раскрытие неопределенностей (правило Лопиталя).

Раскрытие неопределенностей вида .

Будем говорить, что представляет собой при xa неопределенность вида , если

Теорема. (первое правило Лопиталя).

Пусть функции f(x) и g(x) определены и дифференцируемы в проколотой окрестности точки а. Пусть, кроме того, и . Тогда, если существует (конечный или бесконечный), то существует , причем справедливо равенство .

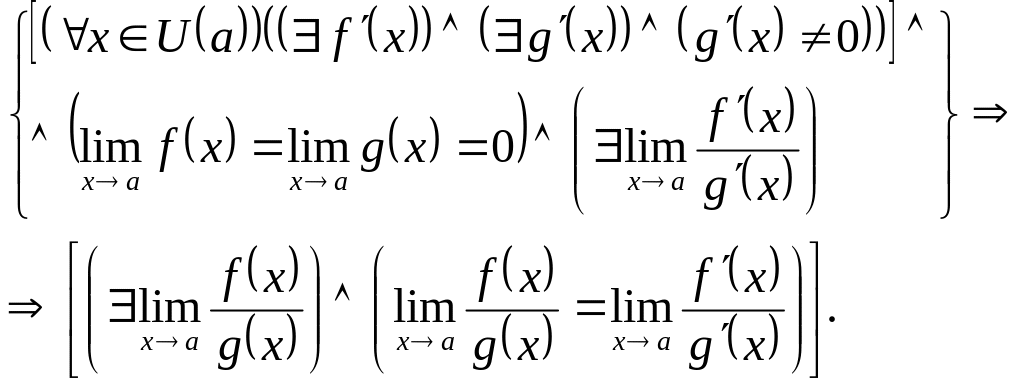
Замечание 1. Предел отношений производных может не существовать, в то время, как предел отношения функций существует.

Пример 1. а=0,

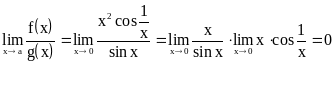
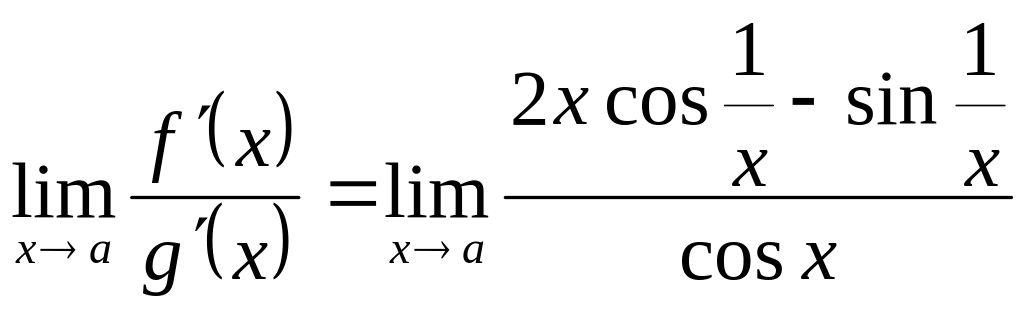не существует, так как 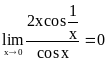, а 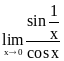не существует (см. пример 4 п.3.17.).

Замечание 2. Если производные обладают теми же свойствами, что и функции f(x) и g(x) , то правило Лопиталя можно применить повторно

Пример 2.

Замечание 3. Правило Лопиталя для неопределенности справедливо для случаев 1) ха+0, 2) ха-0, 3) х  , 4) х  -, 5) х  +.

Раскрытие неопределенностей вида .

Будем говорить, что представляет собой при ха неопределенность вида , если .

Теорема 2. (второе правило Лопиталя).

Пусть функции f(x) и g(x) определены и дифференцируемы в проколотой окрестности точки а и, кроме того, . Пусть, далее, . Тогда, если существует (конечный или бесконечный предел) то существует

Замечание 4. Второе правило Лопиталя также имеет место для случаев 1) ха0, 2) х, 3) х. Изменения в доказательстве аналогичны теореме 1.

Пример 3.

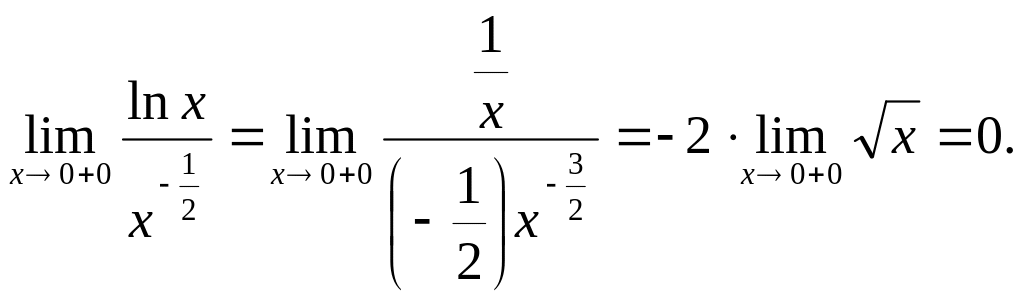
Раскрытие неопределенностей других видов.

Кроме неопределенностей , часто встречаются неопределенности вида: 0, -, 1^, ⁰, 0⁰. Все эти неопределенности сводятся к изученным выше двум неопределенностям. Рассмотрим неопределенность вида -. Пусть имеем выражение f(x)-g(x), причем , тогда 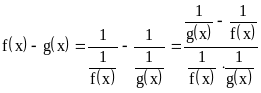, а это неопределенность вида .

Рассмотрим теперь неопределенности типа 1^, 0⁰, ⁰. Каждая из этих неопределенностей имеет вид y=f(x)^g(x), где при xa f(x)1; 0; , a g(x) ; 0; а. Логарифмируя это выражение (считая, что f(x)>0), получим lny=g(x)lnf(x). В любом из трех случаев это выражение представляет собой при ха неопределенность вида 0.

Покажем теперь, как сводить эту неопределенность к виду и . Итак, пусть z=(x) (x), причем

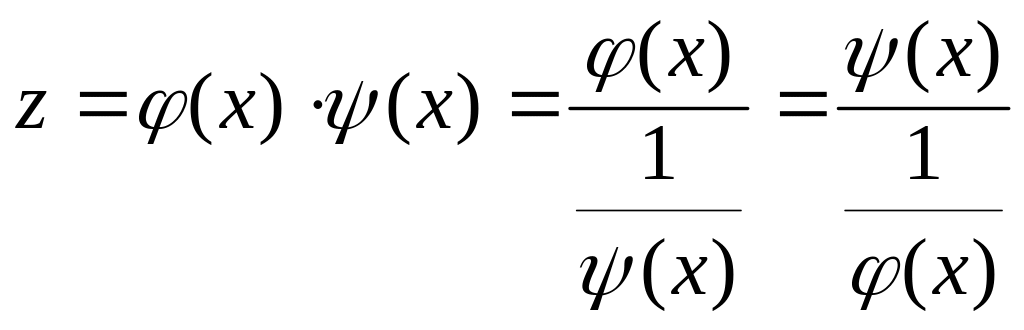. Это неопределенности и .

Пример 4. . Здесь y=x^-2x, тогда

.
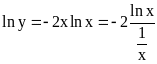
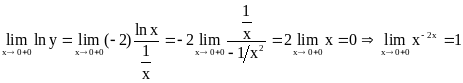