
- •1.5. Дифференциальное исчисление Для замечаний
- •1.5. Дифференциальное исчисление
- •1.5.1. Определение производной
- •1.5.2. Геометрический смысл производной
- •1.5.3. Дифференциируемость функции
- •1.5.4. Правила вычисления производных,
- •1.5.5. Вычисления производных некоторых элементарных функций
- •1.5.6. Правило дифференцирования сложной функции
- •1.5.7. Дифференциал функции
- •1.5.8. Геометрический смысл дифференциала функции
- •1.5.9. Дифференциал независимой переменной
- •1.5.10. Инвариантность формы первого дифференциала
- •1.5.11. Производные высших порядков
- •1.5.12. Дифференциалы высших порядков
- •1.5.13. Дифференцирование функции, заданной параметрически
- •1.5.14. Свойства дифференцируемых функций
- •1.5.14.1. Возрастание (убывание) функций в точке. Локальный экстремум.
- •1.5.14.2. Теорема о нуле производной
- •1.5.14.3. Формула конечных приращений (теорема Лагранжа)
- •1.5.14.4. Обобщенная формула конечных приращений (формула Коши).
- •1.5.14.5. Раскрытие неопределенностей (правило Лопиталя).
- •1.5.14.6. Формула Тейлора с остаточным членом в общей форме (в форме Шлемильха-Роша)
- •1.5.14.7. Остаточный член в форме Лагранжа, Коши, Пеано
- •1.5.14.8. Формула Маклорена
- •1.5.14.8.1. Оценка остаточного члена в форме Лагранжа.
- •1.5.14.8.2. Разложение по формуле Маклорена некоторых элементарных функций
- •1.5.14.8.3. Приложения формулы Маклорена Приближенное вычисление числа е
- •1.5.14.8.4. Вычисление пределов с помощью формулы Маклорена
1.5.6. Правило дифференцирования сложной функции
Теорема. Пусть
1)
задана сложная функция
![]() где x=(t)
и
где x=(t)
и
y=f(x),
2)
функция x=(t)
дифференцируема в точке t0
, а функция y=f(x) дифференцируема в
соответствующей точке x0=(t0).
Тогда сложная функция
![]() дифференцируема в точке t0,
причем
дифференцируема в точке t0,
причем![]()
Замечание.
Обычно
формулу для производной сложной функции
записывают в виде
![]() .
.
Пример
1. Найти
производную функции
![]() Имеем
Имеем
![]() где
x=arctg t. Поэтому
где
x=arctg t. Поэтому
![]()
Пример 2. Найти производную функции
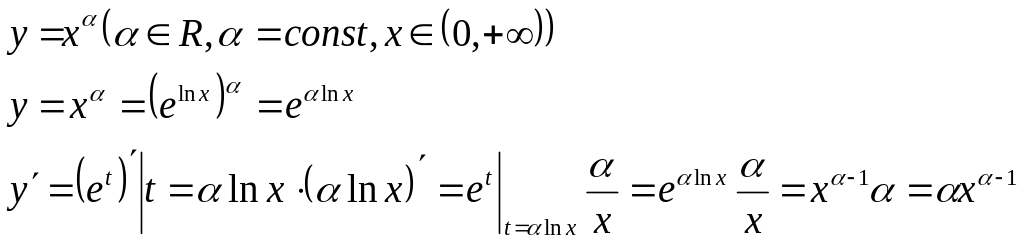
1.5.7. Дифференциал функции
Пусть y=f(x)C1(x), тогда y=x+(x)x (1.)
Если
А,
то слагаемое Аx
есть линейная и однородная относительно
x
функция.*
При x
![]() и поэтому Аx
бесконечно малая того же порядка, что
и x.
и поэтому Аx
бесконечно малая того же порядка, что
и x.
![]() т.е. второе слагаемое x
при x
есть бесконечно малая более высокого
порядка, чем x.
Итак, при А
первое слагаемое Аx
является главной частью приращения
дифференцируемой функции.
т.е. второе слагаемое x
при x
есть бесконечно малая более высокого
порядка, чем x.
Итак, при А
первое слагаемое Аx
является главной частью приращения
дифференцируемой функции.
Определение.
При А
дифференциалом функции y=f(x) в данной
толчке x , соответствующим приращению
аргумента x,
называют главную линейную относительно
x
часть приращения этой функции в точке
x. Символическое обозначение дифференциала
функции
![]() dy.
dy.
Итак,
по определению, dy=Ax
или
![]() (вытекает из теоремы 1 п.4.3.).
(вытекает из теоремы 1 п.4.3.).
Если А=0, то первое слагаемое Ax равенства (1) перестает быть главной частью приращения дифференцируемой функции, ибо Ax=0, а x однако, по договоренности и в этом случае считают
dy= Ax=0.
1.5.8. Геометрический смысл дифференциала функции
|
Пусть дана кривая
y=f(x). Точка М на кривой соответствует
значению аргумента x, а точка Р-(x+x).
МТ - касательная к кривой y=f(x) в точке
М. Очевидно, что y=PN
и
|
щение ординаты кривой, то dy является соответственным приращением ординаты касательной.
1.5.9. Дифференциал независимой переменной
Под дифференциалом dx независимой переменной x понимают любое, не зависящее от x, число, поэтому, по определению, дифференциалом независимой переменной x называют ее приращение x, т.е. полагают, что dx=x.
Введенное определение оправдывается следующими рассуждениями.
Рассмотрим
независимую переменную x как функцию
вида y=x, тогда
![]() .
.
Таким
образом, если аргумент x функции y=f(x)
является независимой переменной, то
![]()
Замечание.
![]() есть число, а
есть число, а
![]() - отношение неопределенных чисел dy и
dx, которые изменяются пропорционально
c
коэффициентом пропорциональности
.
- отношение неопределенных чисел dy и
dx, которые изменяются пропорционально
c
коэффициентом пропорциональности
.
1.5.10. Инвариантность формы первого дифференциала
В предыдущем пункте было показано, что если x есть независимая переменная функции y=f(x), то dy=f(x)dx. Покажем, что эта формула справедлива и в том случае, когда аргумент x является дифференцируемой функцией некоторой новой переменной t. Это свойство дифференциала называется инвариантностью его формы.
Итак,
пусть дана функция
![]() Рассмотрим сложную функцию y=f[(t)].
Если рассматривать здесь t как независимую
переменную, то по определению дифференциала
функции
Рассмотрим сложную функцию y=f[(t)].
Если рассматривать здесь t как независимую
переменную, то по определению дифференциала
функции
![]() (1)
(1)
Аналогично
этому
![]() (2)
(2)
Используя
теорему о сложной функции :
![]() равенство (1) можно переписать в виде
равенство (1) можно переписать в виде
![]() и из (2) имеем
и из (2) имеем
![]()
Итак,
в любом случае дифференциал функции
y=f(x) может быть записан в форме
![]() ,
будет ли x независимой переменной или
нет; разница будет в том, что если за
независимую переменную выбрано t, то dx
означает не произвольное приращение
x,
а дифференциал x как функции от t.
,
будет ли x независимой переменной или
нет; разница будет в том, что если за
независимую переменную выбрано t, то dx
означает не произвольное приращение
x,
а дифференциал x как функции от t.

