ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ.
Дискретная математика.
Лекции.
(для студентов физического факультета)
Чванова А.Н.
доцент кафедры математического анализа
Челябинск 2011г.
Теория графов
Историческая справка.
17 в. – начало использования графов в ходе решения головоломок.
1736 г. – появление теории графов (Эйлер опубликовал 1-ую статью о графах).
19в. – теория графов получила серьёзные применения в химии, биологии, электросхемах и т.д.
30-е гг., 20 в. –теория графов была впервые представлена как отдельная математическая дисциплина в работах венгерского математика Кёнига.
Современные области применения теории графов:
1. теория планирования и управления,
2. теория расписаний,
3. социология,
4. математическая лингвистика,
5. экономика,
6. биология,
7. медицина,
8. электроника,
9. программирование,
11. решение вероятностных и комбинаторных задач
и другие области.
Графы и их простейшие свойства.
Графом на плоскости или в пространстве называется конечное множество точек, некоторые из которых соединены линиями. Эти точки называются вершинами графа, а соединяющие их линии – рёбрами.
Примеры графов:
чёртёж многоугольника,
карта автомобильных дорог,
электросхема,
план предприятия,
блок-схема и др.
Вершина графа называется изолированной, если из неё не выходит ни одного ребра.
Если все вершины графа – изолированные, то он называется «нуль-граф».
Граф называется полным, если любые две его вершины соединены непосредственно ребром, причём желательно, чтобы при этом не было пересечений ребер.
С
войство
полного графа:
Если у полного
графа n
вершин, то число его рёбер
.
Доказать
применяя комбинаторный анализ (количество
сочетаний из n
элементов по 2).
Д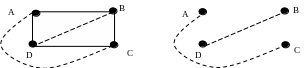
ополнением
данного неполного графа
называется такой новый граф, у которого
вершины те же самые, что и у первого
графа, а рёбрами являются те рёбра,
которые нужно добавить к первому графу,
для того, чтобы он стал полным.
С
тепенью
вершины графа
называется число рёбер, выходящих из
этой вершины.
Степень вершины графа называется чётной (нечётной), если число рёбер, выходящих из этой вершины чётно (нечётно).
Теорема1:
У любого графа сумма степеней всех вершин – есть число чётное, равное удвоенному числу рёбер графа.
Доказательство:
Пусть n- число вершин графа, k – число рёбер.
,
т.к. каждое ребро принадлежит двум
вершинам, следовательно:
. чтд
Следствие:
Число нечётных вершин графа чётно (если сумма n слагаемых – число чётное, то среди них нечётных слагаемых может быть только чётное число)
Задача:
Можно ли 15 телефонов соединить между собой так, чтобы каждый был связан ровно с 9-ю другими?
N=15, стАi = 9.
Выходит противоречие следствию, т.к нечётное число вершин (15) имеют нечётную степень (9).
Ответ: не возможно.
Теорема2:
У любого графа с числом вершин n≥2 имеются хотя бы 2 вершины одинаковой степени.
Доказательство:
Каждому из шахматистов поставим в соответствие вершину графа, соединим рёбрами попарно вершины, соответствующие шахматистам уже сыгравшим между собой партию.
Каждая вершина графа с n вершинами может иметь степень равную 0,1,2,…,(n-1). предположим, что существует граф, все вершины которого имеют разную степень, т.е. каждое из чисел последовательности 0,1,2,…,(n-1) является степенью одной и только одной из его вершин. Но этого не может быть, т.к. если в графе есть вершина А со степенью 0, то в нём не найдётся вершина B cо степенью (n-1), т.к. эта вершина д.б. соединена рёбрами со всеми вершинами, включая вершину A. Т.е. не могут в графе находится одновременно вершины со степенью 0 и (n-1), а значит, не могут все вершины иметь разную степень и есть хотя бы две вершины с одинаковой степенью. чтд
Теорема 3:
Если в графе с n>2 вершинами в точности 2 вершины имеют одинаковую степень, то эти вершины не могут быть степени 0, либо степени (n-1).
Доказательство:
1. Допустим, что всё же найдётся граф с n вершинами, в котором ровно 2 вершины изолированы (т.е. степени 0), а все остальные имеют разные между собой степени. Тогда, если не рассматривать эти две изолирование вершины, останется граф с (n-1) вершинами, степени которых не совпадают. Но такого графа не существует по теореме 2, значит предположение не является верным.
2. Допустим, что существует граф с n вершинами, в котором ровно 2 вершины имеют степень (n-1), а все остальные несовпадающие степени. Рассмотрим дополнение этого графа до полного графа. Тогда эти две вершины (которые имели степень (n-1)) будут иметь степень 0, а этого не может быть из 1-ой части доказательства. чтд