П.2. Примеры уравнений математической физики

1. При изучении различных видов волн – упругих, звуковых, электромагнитных, а также других колебательных явлений приходим к уравнению гиперболического типа – волновому уравнению

, (1.3)

2. Процессы распространения тепла в однородном изотропном теле, так же как и явления диффузии, описываются уравнением параболического типа – уравнением теплопроводности

, (1.4)

2. Математической моделью установившегося теплового состояния в однородном изотропном теле является уравнение эллиптического типа – уравнение Пуассона:

. (1.5)

При отсутствии внутренних источников тепла уравнение (1.5) переходит в уравнение Лапласа

. (1.6)

Потенциалы поля тяготения и стационарного электрического поля также удовлетворяют уравнению Лапласа, в котором отсутствуют соответственно массы и электрические заряды.

Уравнения (1.3) – (1.6) часто называют основными уравнениями математической физики. Их подробное изучение дает возможность построить теорию физических явлений разной природы и решить широкий круг инженерно-технических задач.

П. 3. Постановка задач для уравнений математической физики.

Каждое из уравнений (1.3) – (1.6) имеет бесчисленное множество частных решений. При решении конкретной физической задачи из всех этих решений необходимо выбрать то, которое удовлетворяет некоторым дополнительным условиям, вытекающим из ее физического смысла. Дополнительные условия, заданные на границе исследуемой области, называются граничными или краевыми условиями. А дополнительные условия, относящиеся к моменту времени, с которого начинается изучение данного физического явления, называются начальными условиями.

Для уравнений эллиптического типа задаются только граничные условия. Для уравнений гиперболического и параболического типов задаются одновременно начальные и граничные условия.

Математическая задача, описывающая реальный физический процесс должна удовлетворять трем требованиям – разрешимости, однозначности и непрерывной зависимости от исходных данных (иначе, устойчивости). Задача, удовлетворяющая этим требованиям, называется корректно поставленной задачей. Соблюдение требований корректности постановок задач математической физики обеспечивает физическую содержательность их решения.

П. 4. Постановка задач для уравнения теплопроводности

Тепловые явления играют в природе особую роль, ведь практически все процессы в той или иной степени связаны с изменением температурного состояния и переносом теплоты. Поэтому в дифференциальных уравнениях математической физики исключительное внимание уделяется теории теплообмена, особенно в связи с созданием и развитием аналитических методов решения краевых задач уравнения теплопроводности и ему родственных.

Аналитическое изучение процессов теплопроводности является одним из основных разделов современных инженерных исследований в различных отраслях промышленности, так как целый ряд физических и химико-технологических процессов аналогичен задачам стационарной и нестационарной теплопроводности.

Рассмотрим изотропное твердое тело, температура которого в точке в момент времени определяется функцией . Будем считать тело изотропным в отношении теплопроводности, что означает, что коэффициент внутренней теплопроводности зависит только от точки тела и не зависит от направления нормали к поверхности в этой точке. Пусть в данном теле распространяется тепло, причем, если различные части тела находятся при различной температуре, то в теле будет происходить движение тепла от более нагретых частей к менее нагретым. С помощью закона Фурье можно вывести уравнения распространения тепла в данном теле:

, (1.7)

где – теплоемкость вещества, – его плотность.

Это уравнение называется уравнением теплопроводности неоднородного изотропного тела.

Для полного математического описания процесса распределения тепла в изотропном твердом теле дифференциальное уравнение (1.7) необходимо дополнить условиями однозначности, которые включают в себя

• геометрические условия, характеризующие форму и размеры тела;

• физические условия, характеризующие физические свойства тела и окружающей среды;

• временные условия, определяющие распределение температуры внутри тела в начальный момент времени;

• граничные условия, определяющие взаимодействие тела с окружающей средой.

Начальное условие задает значение искомой функции во всех точках тела в начальный момент времени . Полагая , имеем

, (1.8)

где – известная функция, определенная и непрерывная во всех точках тела.

Граничные условия задаются различными способами в зависимости от температурного режима на границе исследуемой области:

1. граничное условие первого рода – в каждой точке поверхности тела задается значение искомой функции

, (1.9)

где – известная функция, определенная и непрерывная во всех точках поверхности и любой момент времени ;

2. граничное условие второго рода – в каждой точке поверхности тела задается тепловой поток 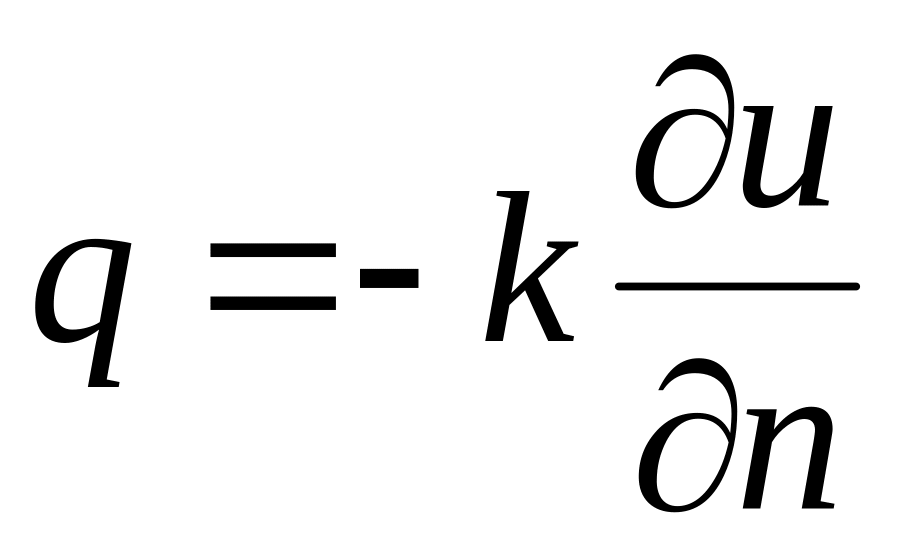, откуда

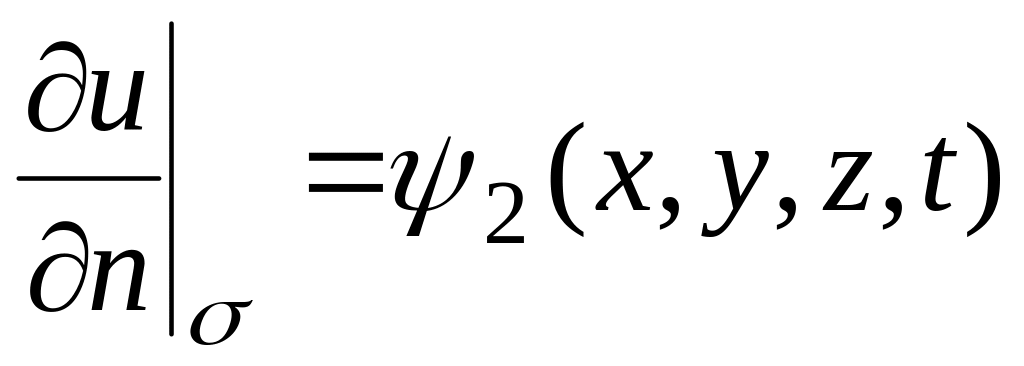3. , (1.10)

где – известная функция, определенная и непрерывная во всех точках поверхности и любой момент времени ;

4. граничное условие третьего рода – на поверхности тела происходит теплообмен с окружающей средой, температура которой 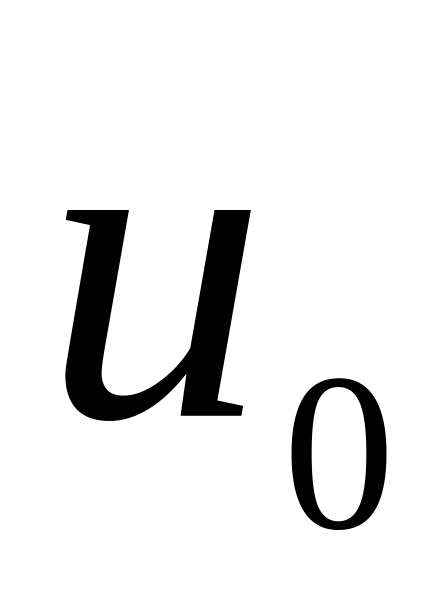известна. По закону Ньютона–Рихмана количество тепла, передаваемое за единицу времени с единицы площади поверхности тела в окружающую среду, пропорционально разности температур поверхности тела и окружающей среды , где – коэффициент теплообмена. По закону сохранения энергии это количество тепла равно количеству тепла, передаваемому через единицу поверхности за единицу времени вследствие внутренней теплопроводности тела. Поэтому на поверхности имеем 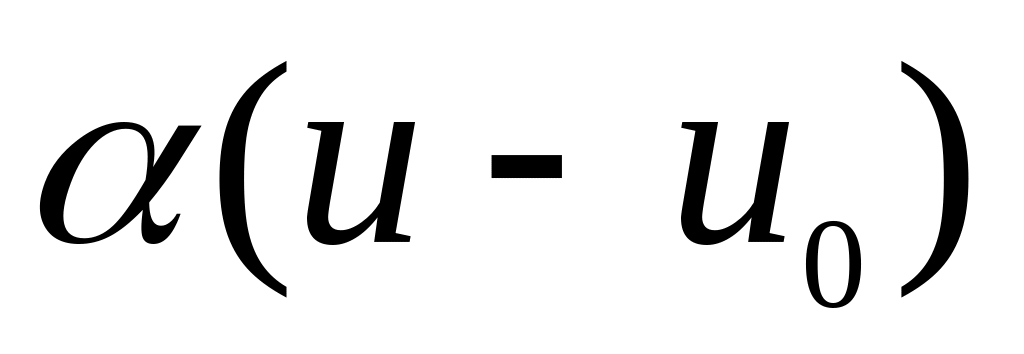= 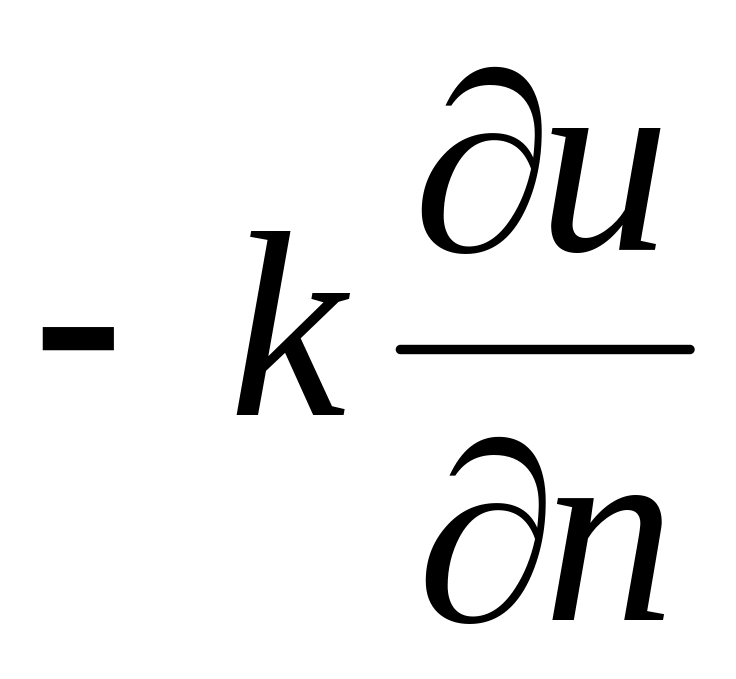. Полагая, 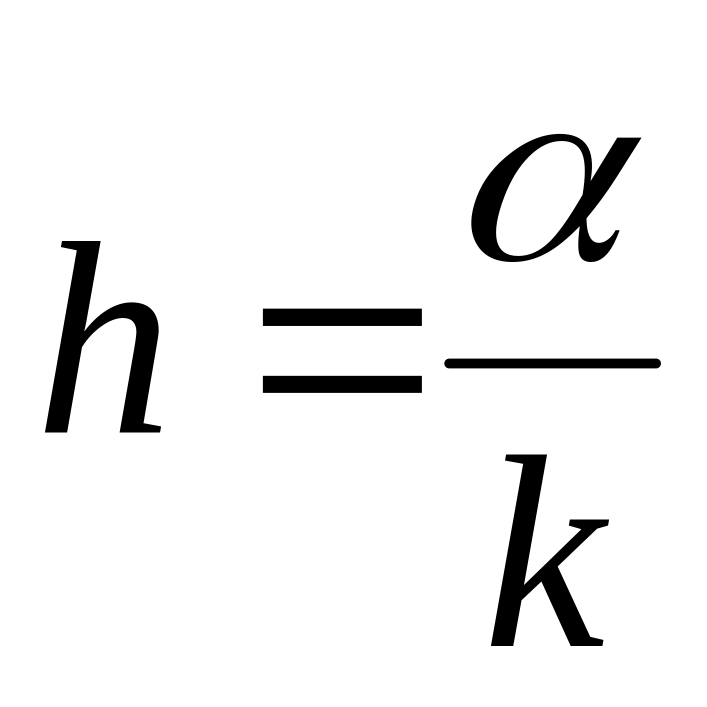, приходим к следующему граничному условию

, (1.11)

где – единичный вектор внешней нормали к поверхности .

Таким образом, задача о распространении тепла в изотропном твердом теле формулируется так: найти решение уравнения теплопроводности (1.7), удовлетворяющее начальному условию (1.8) и одному из граничных условий (1.9), (1.10) или (1.11).