Основные уравнения математической физики. Введение.

Математические задачи, возникающие при изучении различных физических процессов и явлений, содержат много общих элементов и составляют предмет математической физики. Эта отрасль науки и ее методы начали формироваться в XVIII веке при изучении колебаний струны и стержня, при решении задач акустики, гидродинамики и аналитической механики. Новое развитие идеи математической физики получили в XIX веке в связи с задачами теплопроводности, диффузии, упругости, оптики, электродинамики, нелинейными волновыми процессами и теорией устойчивости движения. Круг вопросов, относящихся к математической физике, чрезвычайно широк. В XX веке в нее включаются задачи теории относительности, квантовой физики, новые проблемы газовой динамики, кинетических уравнений, теории ядерных реакторов и физики плазмы.

Постановка задач, связанных с изучением физических проблем, имеет специфические особенности. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов. Основными математическими средствами исследования задач математической физики служат теория дифференциальных уравнений с частными производными, функциональный анализ, численные методы и вычислительная математика.

П. 1. Классификация дифференциальных уравнений с частными производными

Уравнение, связывающее неизвестную функцию , независимые переменные и частные производные от неизвестной функции, называется дифференциальным уравнением с частными производными.

Оно имеет вид

, (1.1)

где – заданная функция своих аргументов.

Порядок старшей производной, входящей в уравнение (1.1), называется порядком уравнения с частными производными.

При решении задач математической физики наиболее часто встречаются дифференциальные уравнения второго порядка.

Решением уравнения с частными производными (1.1) называется всякая функция , которая, будучи подставлена в уравнение вместо неизвестной функции и ее частных производных, обращает это уравнение в тождество по независимым переменным.

Уравнение с частными производными называется линейным, если оно линейно относительно неизвестной функции и ее частных производных.

Так, например, уравнение

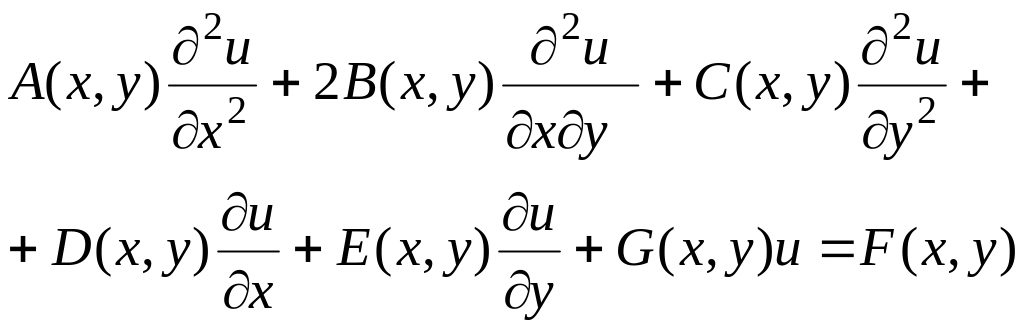(1.2)

есть линейное уравнение второго порядка относительно неизвестной функции , где – функции, имеющие непрерывные производные до второго порядка включительно и не обращаются одновременно в нуль. Если коэффициенты уравнения (1.2) не зависят от и , то оно представляет собой линейное уравнение с постоянными коэффициентами. Уравнение (1.2) называется однородным, если .

Доказано, что любое дифференциальное уравнение вида (1.2) с помощью преобразования независимых переменных и можно привести к каноническому виду. Дифференциальное уравнение (2) принадлежит:

1. гиперболическому типу, если ;

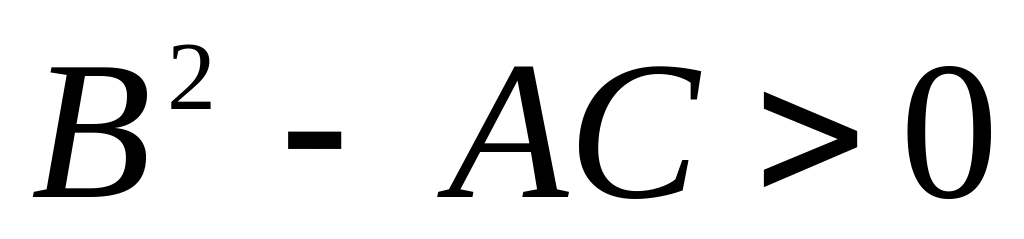2. параболическому типу, если ;

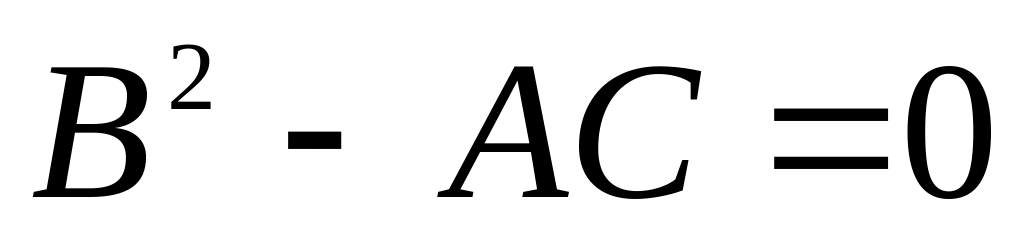3. эллиптическому типу, если .

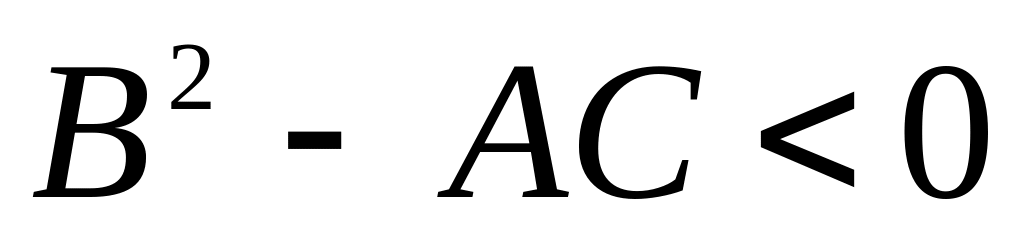Дифференциальные уравнения с частными производными классифицируются и по другому принципу. Одна из независимых переменных искомой функции трактуется как время , а остальные переменные имеют смысл пространственных координат. Если в записи уравнения (1.2) нет переменной , то оно называется стационарным и описывает физические процессы, установившиеся во времени (уравнение эллиптического типа). При наличии в записи уравнения переменной оно описывает процессы, развивающиеся во времени, и называется нестационарным (уравнения гиперболического и параболического типов).

Для каждого типа канонических уравнений разработаны определенные методы как аналитического, так и численного решения.