
- •Раздел 2. Кинематика.
- •Тема 1. Введение в кинематику
- •Тема 2. Кинематика точки
- •Способы задания движения точки. Скорость и ускорение
- •Тема 3. Простейшие движения твердого тела. Поступательное движение твердого тела
- •Тема 4. Сложное движение точки
- •Тема 5. Плоское движение твердого тела.
- •Тема 6. Движение твердого тела вокруг неподвижной точки. (сферическое движение)
- •Тема 7. Движение свободного твердого тела.
- •Тема 8. Сложное движение твердого тела
- •1. Вращения имеют одинаковые направления
- •2. Вращения имеют противоположные направления с неравными угловыми скоростями
- •3. Пара вращений (вращения имеют противоположные направления с равными угловыми скоростями)
- •1. Скорость поступательного движения перпендикулярна оси относительного движения
- •2. Скорость поступательного переносного движения параллельна вектору угловой скорости относительного вращения
- •3. Скорость поступательного переносного движения направлена под углом к вектору угловой скорости относительно вращательного движения
Тема 5. Плоское движение твердого тела.
П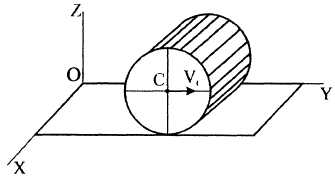 лоским
или плоскопараллельным называют
такое движение твердого
тела, при котором все его точки перемещаются
в плоскостях,
параллельных некоторой неподвижной
плоскости.
лоским
или плоскопараллельным называют
такое движение твердого
тела, при котором все его точки перемещаются
в плоскостях,
параллельных некоторой неподвижной
плоскости.
П
Рисунок 1
Уравнения плоского движения твердого тела
Д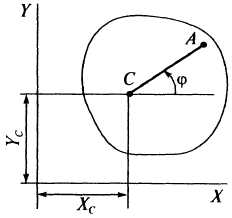 ля
задания движения сечения твердого тела
достаточно описать движение какого-либо
отрезка
ля
задания движения сечения твердого тела
достаточно описать движение какого-либо
отрезка
![]() ,
принадлежащего этому сечению. Положение
отрезка
определяется координатами точки
,
принадлежащего этому сечению. Положение
отрезка
определяется координатами точки
![]() ,
выбранной за полюс, и углом поворота
отрезка, который отсчитывается от
выбранного начального положения (рис.
2). Тогда уравнениями плоского движения
твердого тела будут
,
выбранной за полюс, и углом поворота
отрезка, который отсчитывается от
выбранного начального положения (рис.
2). Тогда уравнениями плоского движения
твердого тела будут
Рисунок 2![]()
![]() ,
,
![]() (1)
(1)
Выражения
![]() ,
,
![]() формулы (1) описывают поступательное
движение плоской фигуры, определяемое
движением полюса
Поступательное движение плоской фигуры
зависит от выбора полюса. Если выбрать
за полюс точку
формулы (1) описывают поступательное
движение плоской фигуры, определяемое
движением полюса
Поступательное движение плоской фигуры
зависит от выбора полюса. Если выбрать
за полюс точку
![]() ,
то выражения
,
будут иметь другой вид. Выражение
,
то выражения
,
будут иметь другой вид. Выражение
![]() формулы
(1) описывает вращательное
движение плоской фигуры, которое
не зависит от выбора полюса.
формулы
(1) описывает вращательное
движение плоской фигуры, которое
не зависит от выбора полюса.
Скорость точек плоской фигуры
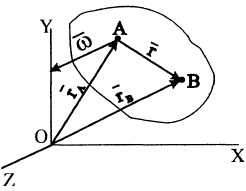
Определим положение точки
![]() в выбранной системе отсчета, принимая
за полюс точку
(рис. 3):
в выбранной системе отсчета, принимая
за полюс точку
(рис. 3):
![]() (2)
(2)
Вектор
![]() постоянного модуля (расстояние между
точками
и
не изменяется) меняет свое направление
вследствие вращения плоской фигуры.
Дифференцируем формулу (2) по времени:
постоянного модуля (расстояние между
точками
и
не изменяется) меняет свое направление
вследствие вращения плоской фигуры.
Дифференцируем формулу (2) по времени:
![]()
 ,
где
,
где
![]() — скорость выбранной точки
;
— скорость выбранной точки
;
Рисунок 3![]()
![]() — скорость точки
во вращательном
движении вокруг полюса
,
которую определим по
формуле Эйлера:
— скорость точки
во вращательном
движении вокруг полюса
,
которую определим по
формуле Эйлера:
![]() .
.
В
соответствии с правилом векторного
произведения вектор
![]() лежит
в плоскости фигуры, перпендикулярен
лежит
в плоскости фигуры, перпендикулярен
![]() (
(![]() )
и
направлен в сторону вращения плоской
фигуры, т. е. в соответствии
с направлением
)
и
направлен в сторону вращения плоской
фигуры, т. е. в соответствии
с направлением
![]() .
Модуль вектора
равен:
.
Модуль вектора
равен:
![]() .
Так
как
.
Так
как
![]() ,
то
,
то
![]() .
Поэтому
.
Поэтому
![]() .
Получим
.
Получим
![]() ,
(3)
,
(3)
или
![]() ,
(4)
,
(4)
Скорость любой точки тела в плоском движении равна геометрической сумме скорости полюса и скорости этой точки во вращательном движении вместе с телом вокруг полюса.
Так как вектор скорости перпендикулярен отрезку, соединяющему точки и , то из этого вытекает следствие.
Проекции скоростей двух точек твердого тела на прямую, соединяющие эти точки, равны между собой. При этом проекции должны иметь одинаковый знак.
Мгновенный центр скоростей
М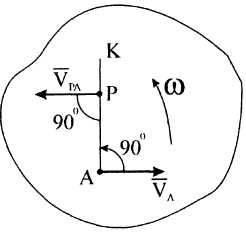 гновенным
центром скоростей (МЦС) называется точка
в плоскости движения плоской фигуры,
скорость которой в данный момент равна
нулю.
гновенным
центром скоростей (МЦС) называется точка
в плоскости движения плоской фигуры,
скорость которой в данный момент равна
нулю.
Д
Рисунок 4![]() .
Повернем вектор
.
Повернем вектор
![]() на 90° по направлению вращения и проведем
луч
на 90° по направлению вращения и проведем
луч
![]() .
От точки
отложим отрезок
.
От точки
отложим отрезок
![]() :
:![]() .
.
Определим
скорость точки
![]() во вращательном движении вокруг точки
,
приняв ее за полюс:
во вращательном движении вокруг точки
,
приняв ее за полюс:
![]() .
Вектор
.
Вектор
![]() перпендикулярен
и направлен
в соответствии с угловой скоростью
(рис. 4), т. е.
перпендикулярен
и направлен
в соответствии с угловой скоростью
(рис. 4), т. е.
![]() .
Запишем
уравнение (3) теоремы о сложении
скоростей плоской фигуры для точки Р,
приняв
за полюс точку
А:
.
Запишем
уравнение (3) теоремы о сложении
скоростей плоской фигуры для точки Р,
приняв
за полюс точку
А:
![]()
Скорость
точки
равна нулю, следовательно, точка
является МЦС. Если за полюс выбрать
точку
,
то уравнение (3) принимает вид
![]() .
.
Однако
![]() ,
,
![]() ,
тогда
,
тогда
![]() (5)
(5)
И
Рисунок 5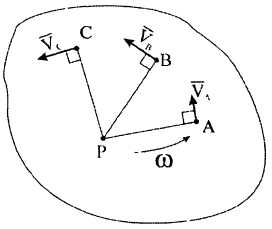
![]() ,
,
![]() ,
,
![]() .
.
Откуда
![]() .
.
Отношение скорости любой точки плоской фигуры к ее расстоянию до МЦС является величиной, равной угловой скорости вращения.
Если известны направления векторов скоростей двух точек плоской фигуры, то МЦС находится в точке пересечения перпендикуляров, проведенных к векторам скоростей в точках их приложения.
Если известны МЦС и угловая скорость вращения, то вектор скорости любой точки будет перпендикулярен отрезку, соединяющему МЦС с данной точкой, и направлен в соответствии с угловой скоростью. Модуль скорости равен произведению угловой скорости на расстояние от точки до МЦС.
Ч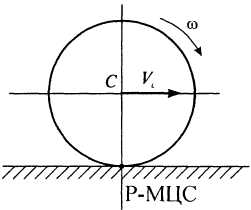 астные
случаи определения МЦС
астные
случаи определения МЦС
а)
Колесо
катится без скольжения. МЦС
находится в точке соприкосновения
колеса с неподвижной поверхностью
(рис. 6).
![]() .
.
б
Рисунок 6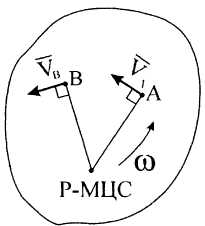 )
Известны скорости двух точек или величина
и направления скорости одной точки
)
Известны скорости двух точек или величина
и направления скорости одной точки
![]() и направление другой.
Для нахождения МЦС
проводим перпендикуляры к
векторам скоростей в точках
и
.
Точка пересечения
перпендикуляров будет МЦС (рис.
7).
и направление другой.
Для нахождения МЦС
проводим перпендикуляры к
векторам скоростей в точках
и
.
Точка пересечения
перпендикуляров будет МЦС (рис.
7).
Рисунок 7![]()
 ;
;
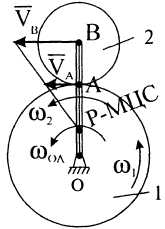
в) Известны скорости точек и механизма
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
М
Рисунок 8![]() вращаются вокруг
точки
.
Колесо 2
совершает плоское
движение (рис. 8).
вращаются вокруг
точки
.
Колесо 2
совершает плоское
движение (рис. 8).
![]() ,
,
![]() ,
,
![]()
или
![]() .
Откладываем
на прямой
отрезок
и
получаем точку
(МЦС).
.
Откладываем
на прямой
отрезок
и
получаем точку
(МЦС).
![]() .
.
Н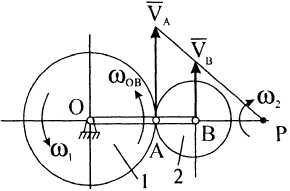 аправление
угловой скорости
аправление
угловой скорости
![]() определяется направлениями скоростей
(рис. 8).
определяется направлениями скоростей
(рис. 8).
г)
Известны угловая скорость кривошипа
![]() и
угловая скорость
колеса 1:
и
угловая скорость
колеса 1:
Рисунок 9![]()
Колесо
1
и кривошип
вращаются
вокруг точки
![]() .
Колесо
2
совершает
плоское движение:
,
.
Колесо
2
совершает
плоское движение:
,
![]() ,
,
![]() .
.
Откладываем на прямой
![]() отрезок
отрезок
![]() и получаем точку
(МЦС).
и получаем точку
(МЦС).
![]() .
.
Направление угловой скорости определяется векторами скоростей (рис. 9).
д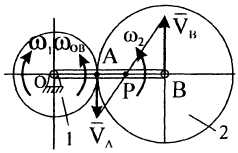 )
Известно, что векторы скоростей точек
и
параллельны
и
противоположно направлены.
)
Известно, что векторы скоростей точек
и
параллельны
и
противоположно направлены.
, .
К
Рисунок 10
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Направление
угловой скорости
![]() определяется векторами скоростей (рис.
10).
определяется векторами скоростей (рис.
10).
е)
Четырехзвенник
![]() занимает положение, показанное на рис.
11,
занимает положение, показанное на рис.
11,
![]() ,
,
![]() .
Вектор скорости
.
Вектор скорости
![]() перпендикулярен
и направлен в соответствии с угловой
скоростью. Скорость точки
также перпендикулярна
перпендикулярен
и направлен в соответствии с угловой
скоростью. Скорость точки
также перпендикулярна
![]() ,
так как звенья
и
,
так как звенья
и
![]() совершают вращательное движение.
Стержень
совершает плоское движение. Строим МЦС
стержня
.
Перпендикуляры к скоростям точек
и
будут параллельны, т. е. пересекаются в
бесконечности. Поэтому МЦС не существует.
совершают вращательное движение.
Стержень
совершает плоское движение. Строим МЦС
стержня
.
Перпендикуляры к скоростям точек
и
будут параллельны, т. е. пересекаются в
бесконечности. Поэтому МЦС не существует.
С
Рисунок 11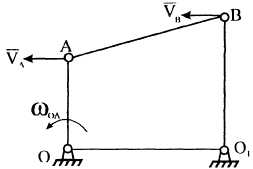
![]() .
.
Ускорения точек плоской фигуры
Для определения ускорения дифференцируем формулу (4) по времени:
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Т огда
огда
![]() ,
где
,
где
![]() —
вращательное ускорение
точки
во
вращательном движении
плоской фигуры вокруг полюса
;
—
вращательное ускорение
точки
во
вращательном движении
плоской фигуры вокруг полюса
;
![]() —
центростремительное
ускорение точки
во
вращательном
движении плоской фигуры вокруг полюса
.
—
центростремительное
ускорение точки
во
вращательном
движении плоской фигуры вокруг полюса
.
В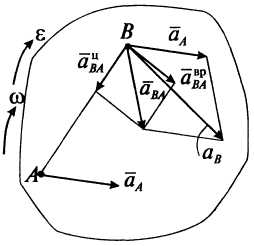 екторы
екторы
![]() и
и
![]() в
соответствии с правилом векторного
произведения
будут направлены следующим образом
(рис. 12).
в
соответствии с правилом векторного
произведения
будут направлены следующим образом
(рис. 12).
В
Рисунок 12
![]() ,
,
![]() .
.
Получим
![]() (6)
(6)
или
![]() (7)
(7)
Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения данной точки во вращательном движении плоской фигуры вокруг полюса.
Для нахождения модуля ускорения точки следует спроектировать уравнение (6) на выбранные оси координат.
Мгновенный центр ускорений
Мгновенный центр ускорений (МЦУ) — это точка в плоскости движения плоской фигуры, ускорение которой равно нулю.
Д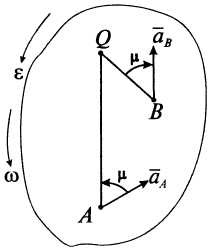 ля
построения МЦУ при известных ускорении
точки плоской фигуры, угловой скорости
и ускорении необходимо (рис. 13):
ля
построения МЦУ при известных ускорении
точки плоской фигуры, угловой скорости
и ускорении необходимо (рис. 13):
Определить угол
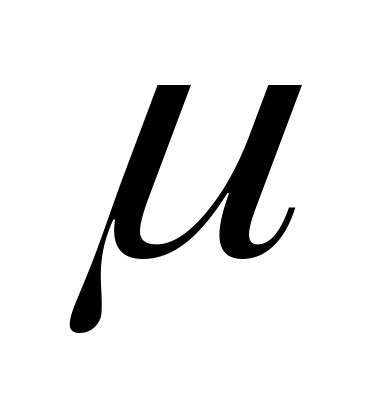 по формуле:
по формуле:
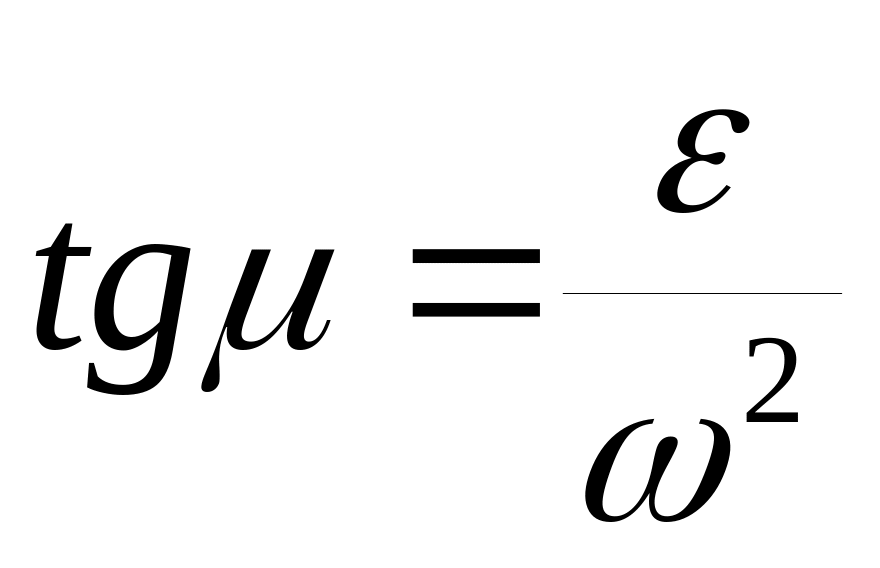 .
.Повернуть вектор ускорения точки на угол в направлении углового ускорения.
О
Рисунок 13
тложить отрезок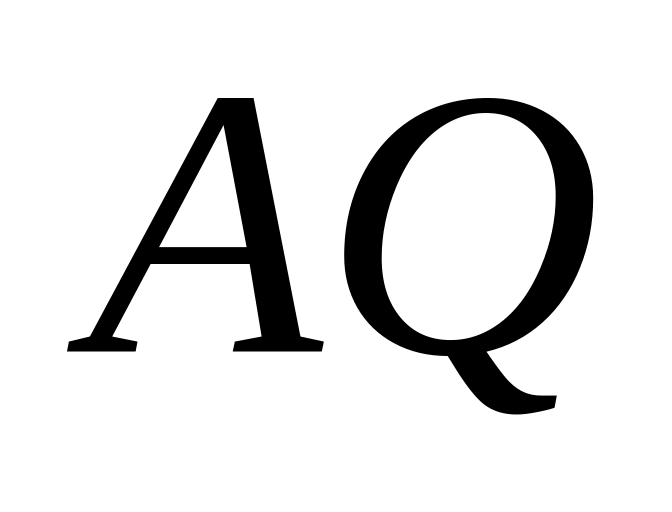 :
:
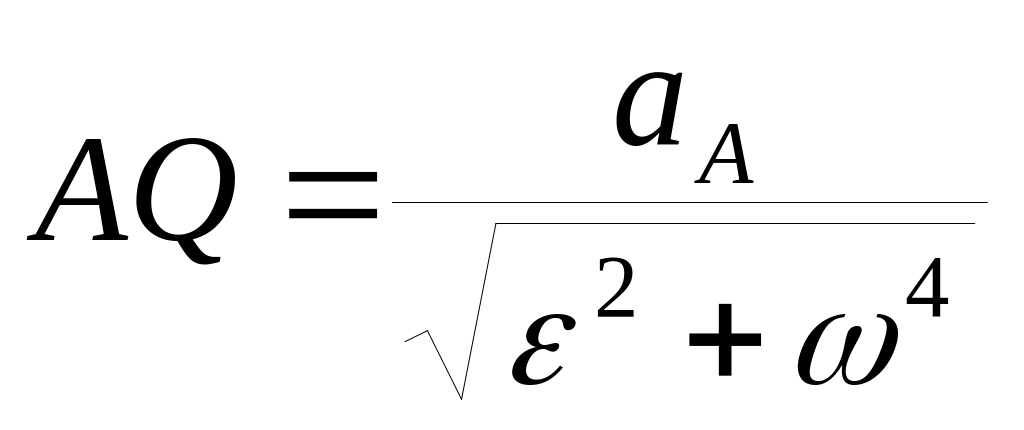 по направлению повернутого
вектора ускорения
по направлению повернутого
вектора ускорения
 .
.
С помощью
МЦУ можно найти ускорение любой точки.
Для этого находим величину
ускорения точки
:
![]() .
От отрезка
.
От отрезка
![]() под
углом
откладываем в направлении,
противоположном угловому ускорению,
вектор ускорения точки
(рис.
13). МЦУ
и МЦС в общем случае — разные
точки.
под
углом
откладываем в направлении,
противоположном угловому ускорению,
вектор ускорения точки
(рис.
13). МЦУ
и МЦС в общем случае — разные
точки.
