2.3. Электродинамика

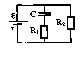
Пример 3.1. (С3). Чему равен электрический заряд на обкладках конденсатора электроемкостью С = 1000 мкФ (см. рисунок), если внутреннее сопротивление источника тока r =10 Ом, ЭДС его 30 В, а сопротивления резисторов R₁ = 40 Ом и R₂ = 20 Ом?

Особенностью схемы в рассматриваемом нами примере является включение в нее конденсатора, который не пропускает ток по сопротивлению R₁. При решении задачи необходимо было учесть, что значения напряжения на конденсаторе и параллельно подсоединенном резисторе одинаковы и равны U = IR₂, U = Ed, где Е — напряженность поля в конденсаторе. Отсюда d = 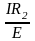. Согласно закону Ома, I = . Следовательно, d = .

П ример 3.2. (С3). До замыкания ключа К на схеме (см. рисунок) идеальный вольтметр V показывал напряжение 7 В. Внутреннее сопротивление источника 0,75 Ом. Что показывает идеальный амперметр А после замыкания ключа? Сопротивления резисторов указаны на рисунке.

Решение задачи предполагает расчет сопротивления внешней цепи, подсоединенной к ЭДС, R= 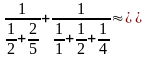2,24 Oм. (1)

По условию задачи до замыкания ключа вольтметр показывает значение ЭДС ε = 7 В. (2)

П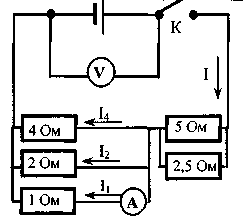 осле замыкания ключа ЭДС рассчитывается по закону Ома для полной цепи ε = I(r + R), (3)

где r - внутреннее сопротивление источника. Так как при параллельном соединении ток распределяется обратно пропорционально сопротивлениям (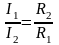 = 2 => I₂ = 0,5 I₁ и т.д.), то

I = I₁ + 0,5I₁+ 0,25I₁ = 1,75I₁ (4). Подставляя (1) (2) (4) в (3), находим

I₁ = = 1,3 А .

Пример 3.3. (С3) В закрытом сосуде вместимостью 20 л находится воздух при нормальных условиях. Воздух начали греть электрическим нагревателем, и через 10 мин давление в сосуде повысилось до 4·10⁵ Па. Какова сила тока в нагревателе, если известно, что КПД нагревателя 13 %, и он работает при напряжении 100 В? Удельная теплоемкость воздуха в данных условиях равна 716 Дж/(кг·К), а его плотность при нормальных условиях равна 1,29 кг/м³.

Начало решения составляет формула для расчета КПД нагревателя:

η =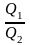 , где Q₁ = сm(Т₂-Т₁); Q₂ = IUt.

Применение закона Шарля позволяет рассчитать температуру Т₂ =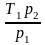 . Следовательно, η = . С учетом того, что m = ρV, рассчитывается значение искомой величины: I = .

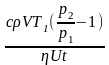Пример 3.4. (С3)

По прямому горизонтальному проводнику длины L = 1 м с площадью поперечного сечения S = 1,25·10^-5 м², подвешенному с помощью двух одинаковых невесомых пружинок с коэффициентами упругости k, течет электрический ток I = 10 А. При включении вертикального магнитного поля с индукцией В = 0,1 Тл проводник отклоняется так, что оси пружинок составляют с вертикалью угол а (см. рисунок). Абсолютное удлинение каждой из пружинок при этом составляет Δl= 7·10^-3 м. Каков коэффициент упругости каждой из пружинок? (Плотность материала проводника

ρ = 8·10³ кг/м³.)

Запись условия механического равновесия проводника в проекции на ось Х и У приводит к системе уравнений:

2k Δl cos α = mg,

2k Δl sin α = IBL.

Возведение обоих равенств в квадрат и их сложение дает возможность рассчитать искомую величину: (2k Δl)² = (mg)² + (IBL)², отсюда k = . С учетом того, что масса провода m = ρ LS, результат имеет вид k = .

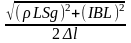Закон электромагнитной индукции являлся стержневым в четырёх группах заданий: пятой, шестой, седьмой и восьмой (примеры 3.5; 3.6; 3.7 и

Пример 3.5. (С4). Металлическое кольцо, диаметр которого 20 см, а диаметр провода кольца 2 мм, расположено в магнитном поле, магнитная индукция которого меняется по модулю со скоростью 1,09 Тл/с. Плоскость кольца перпендикулярна вектору магнитной индукции. Возникающий в кольце индукционный ток 10 А. Определите удельное сопротивление металла, из которого изготовлено кольцо.

ЭДС индукции в кольце ε = -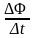 . Изменение магнитного потока за время Δt равно ΔФ = Δ(BS), где S (площадь кольца) постоянна и равна S = . Следовательно, |ε| = S . По закону Ома для участка цепи ε = IR = I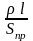 , где S_np - площадь сечения медного провода кольца S_np =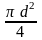 , длина кольца l = πD. Сочетание всех этих формул позволяет найти искомую величину, а расчет позволяет определить материал проводника:

ρ = ≈1,7·10^-8 Oм·м.

Сравнение полученного значения удельного сопротивления с табличным значением этой величины позволяет выявить материал проводника: медь.

Пример 3.6. (С4). Плоская горизонтальная фигура площадью S = 0,1 м², ограниченная проводящим контуром, имеющим сопротивление R = 5 Ом, находится в однородном магнитном поле. Какой заряд протечет по контуру за большой промежуток времени, пока проекция магнитной индукции на вертикаль равномерно меняется с B_1z = 2 Тл до B_2z = - 2 Тл ?

Для решения этой задачи достаточно было использовать закон электромагнитной индукции для случая однородного поля по закону электромагнитной индукции . С другой стороны, |ε_i | = IR. Поэтому |Δq| = IΔt = 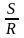|В_2z – B_1z|.

В отличие от примера 3.6, где условие задачи несколько упрощено тем, что плоская фигура не вращалась, в примере 3.7 (седьмая группа задач) катушка вращается. Поэтому поток магнитной индукции в этом случае изменяется благодаря изменению угла поворота катушки (угла между нормалью к плоскости катушки и линиями магнитной индукции).

Пример 3.7. (С4) Плоская катушка диаметром 6 см, состоящая из 120 витков, находится в однородном магнитном поле. Катушка поворачивается вокруг оси, перпендикулярной линиям магнитной индукции, на угол 180° за 0,2 с. Плоскость катушки до и после поворота перпендикулярна линиям магнитной индукции. Чему равна индукция магнитного поля, если среднее значение ЭДС индукции, возникающей в катушке, 0,2 В?

Подобно предыдущим типам задач, решение данной задачи предполагает знание закона электромагнитной индукции. ЭДС индукции в катушке: ε = -n . Изменение магнитного потока за время Δt равно ΔФ = Ф₂ – Ф₁= BS(cos α₂ – cos α₁), где S= , cos α₂ = -1, cos α₁ = +1.

Следовательно, ΔФ = -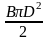 . ε =- n . B = .

Пример 3.8. (С6) Квадратную рамку из медной проволоки со стороной b = 5 см и сопротивлением R = 0,1 Ом перемещают вдоль оси Ох по гладкой гор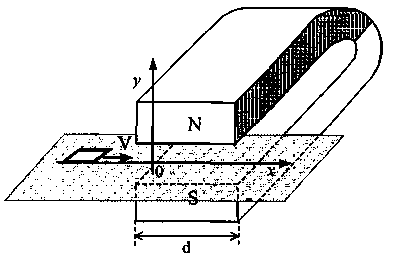 изонтальной поверхности с постоянной скоростью V = 1 м/с. Начальное положение рамки изображено на рисунке. За время движения рамка успевает пройти между полюсами магнита и оказаться в области, где магнитное поле отсутствует. Индукционные токи, возникающие в рамке, оказывают тормозящее действие, поэтому для поддержания постоянной скорости движения к ней прикладывают внешнюю силу F, направленную вдоль оси Ох. Чему равна суммарная работа внешней силы за время движения рамки? Ширина полюсов магнита d = 20 см, магнитное поле имеет резкую границу, однородно между полюсами, а его индукция В = 1 Тл.

При решении такого рода задач необходимо было учесть, что при пересечении рамкой границы области поля со скоростью V изменяющийся магнитный поток создает ЭДС индукции ε_инд =- = VBb. Сила тока в это время равна I=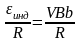 . Однако при движении рамки под действием внешней силы в ней возникает тормозящая сила Ампера F_A = IBb = V . Так как рамка по условию задачи движется прямолинейно и равномерно, то сила Ампера равна по модулю внешней силе: F_A = F. Ток течет в рамке только во время изменения магнитного потока, т.е. при входе в пространство между полюсами и при выходе. За это время рамка перемещается на расстояние х = 2b, а приложенная внешняя сила совершает работу А = F·х = 2Fb. Подставляя значение силы, получаем конечный результат решения в общем виде: А = 2V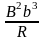 .