7.2 Интегрирование некоторых тригонометрических функций
Значительное количество интегралов от тригонометрических функций найти аналитически нельзя. Вместе с тем, есть функции, которые могут быть проинтегрированы аналитически. Выделим несколько случаев.
1. Интеграл произведения синусов и косинусов
различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
Примеры.
1)
2)
.
2. Интегралы вида
,
и
,
где
- целые, неотрицательные, четные
числа
вычисляют, руководствуясь следующим правилом:
Понижают степень функции на основании формул:
,
,
,
применяя их необходимое количество раз.
Примеры. Найти интегралы
1)
Согласно правилу, имеем
.
2)
.
В данном примере указанное правило было применено дважды.
3)
.
3. Интегралы вида
,
и
,
где
(и/или
)
- положительное, нечетное число
вычисляют, руководствуясь следующим правилом:
Интегралы от нечетной степени синуса или косинуса можно найти путем отделения от нее одного множителя в первой степени (с последующим внесением под знак дифференциала) и замены другого множителя в оставшейся степени кофункцией.
Примеры. Найти интегралы
1)
Воспользуемся тем, что
и
.
Тогда
.
2)
Как и в предыдущем примере, и .
Тогда, согласно правилу, имеем
.
3)
Подынтегральная функция
содержит
в нечетной степени. Поэтому в числителе
отделяем
и на основании того, что
и
,
вычислим интеграл:
.
4. Интегралы вида ,
где и - целые числа и хотя бы одно из них отрицательное
Здесь единой рекомендации нет. Выделим следующие случаи:
а) В подынтегральной функции степень
числителя на единицу меньше степени
знаменателя, например
,
,
и т.д.
В этом случае применяют интегрирование по частям (см. пример 4 в параграфе 5.4).
б) В подынтегральной функции степень
числителя меньше степени знаменателя
на две единицы, например
,
,
и т.д. Такие интегралы сводятся к
или к
.
Примеры:
1)
.
2)
.
в) В подынтегральной функции степень
числителя меньше степени знаменателя
на
(
)
единиц, например
,
,
и т.д.
В этом случае следует увеличить степень
числителя, умножив его на выражение
,
равное единице.
Иногда при интегрировании таких тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций (см. ниже пример 3).
Примеры:
1)
Каждое из слагаемых вычисляется по предыдущему правилу:
.
2)
.
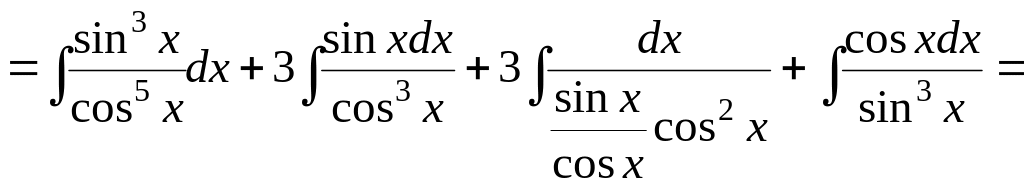
3)
5. Интеграл вида
.
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы этого вида вычисляются с
помощью универсальной тригонометрической
подстановки
.
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
,
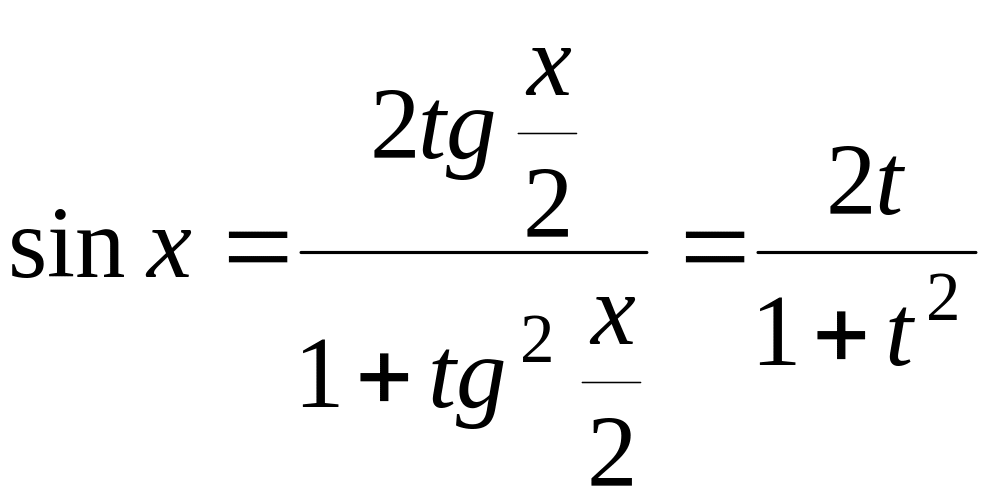Тогда
.
Таким образом требуется вычислить интеграл вида:
и затем вернуться к исходной переменной.
Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.
Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.
Примеры.
1)
.
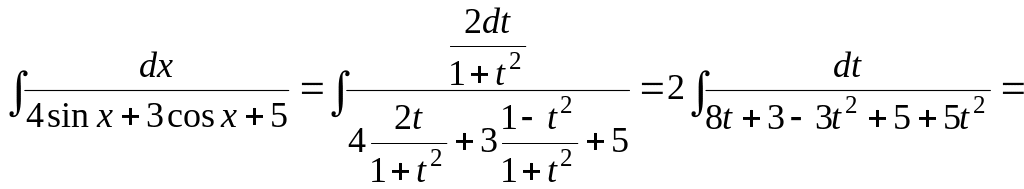
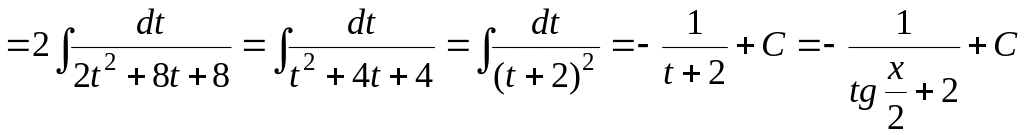2)
.
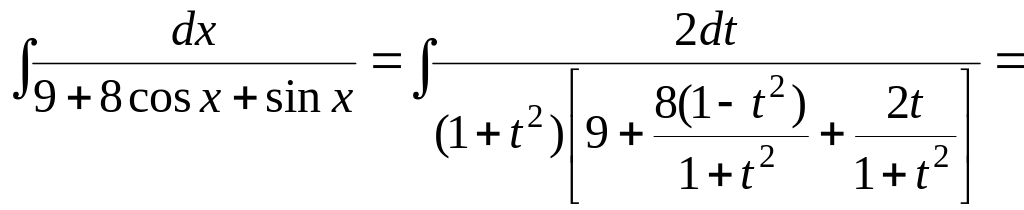
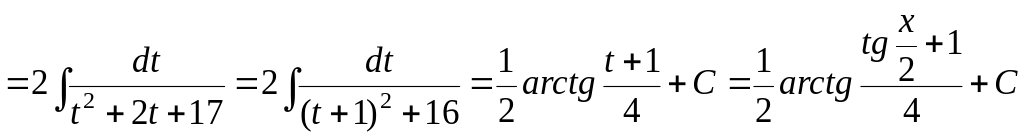6. Интеграл вида ,
если функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
Функция
в числителе может содержать cosx
только в четных степенях, а, следовательно,
может быть преобразована в рациональную
функцию относительно sinx.
Пример.
.
Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
7. Интеграл вида ,
если функция R является нечетной относительно sinx.
По аналогии с рассмотренным выше случаем выполняется подстановка
t = cosx.
Тогда
Пример.
.
8. Интеграл вида ,
если функция R - четная относительно sinx и cosx.
Для преобразования функции R в рациональную используется подстановка
t = tgx.
Тогда
Пример.
.
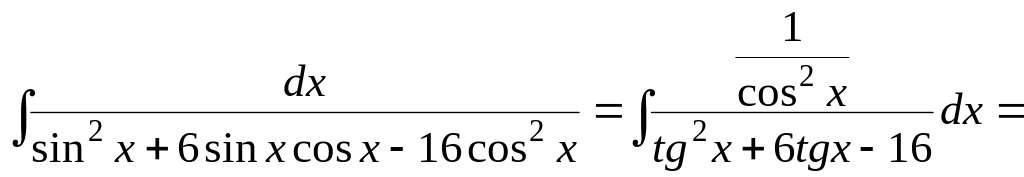
8. Иногда применяются некоторые нестандартные приемы.
Пример.
В результате интегрирования по частям получили выражение:
,
перенеся интеграл из правой части в левую, находим значение:
.
Возвращаясь к исходной переменной х, получаем:
или
.