5.4 Метод интегрирования по частям

Метод интегрирования по частям основан на применении формулы дифференцирования произведения двух функций:

где u и v – некоторые функции от х.

В дифференциальной форме: .

Проинтегрировав, получаем: ,

а в соответствии со свойствами неопределенного интеграла:

или .

Эта формула называется формулой интегрирования по частям в неопределенном интеграле. В качестве функции u(x) принимается функция, которая дифференцированием упрощается, или трансцендентные функции lnx, arctg x, arcsin x. А именно:

1) Интегралы вида , , ,

где – многочлен, вычисляются интегрированием по частям, причем следует взять , а оставшееся выражение взять за .

2) Интегралы вида , , ,

где - многочлен, также вычисляются интегрированием по частям, но здесь за следует взять , , , а оставшееся выражение взять за .

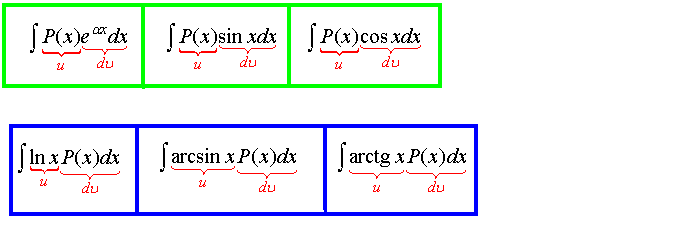
Примеры: вычислить интегралы.

1)

Применим формулу интегрирования по частям:

.

Таким образом, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

2)

.

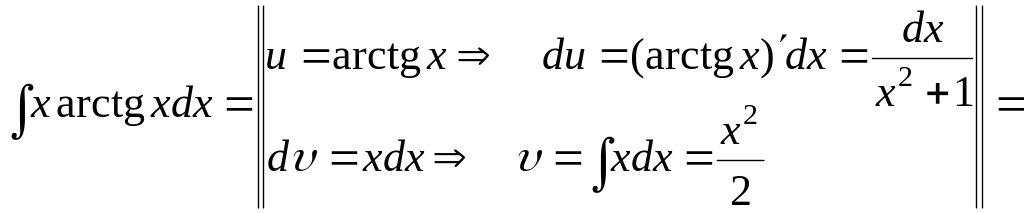
3)

Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.

4)

Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.

Примеры на различные основные методы интегрирования.

1)

2)

3)

4)

5)

6)

.

7)

8)

9)

10)

6. Интегрирование некоторых функций, содержащих квадратный трехчлен

Рассмотрим интегралы следующих типов:

1) , где или

2) , где или

3) ,

4) , где ,

Квадратный трехчлен в этих интегралах не имеет действительных корней.

Общие рекомендации по вычислению интегралов приведенных типов:

В интеграле выделить из квадратного трехчлена полный квадрат.

В интеграле в числителе выделить производную квадратного трехчлена знаменателя.

В интеграле вынести из-под корня .

В интеграле в числителе выделить производную квадратного трехчлена знаменателя и воспользоваться рекуррентной формулой:

,

где ; .

Поясним эти рекомендации на примерах.

Примеры.

1)

Данный интеграл – интеграл первого типа при . Выделим полный квадрат в знаменателе дроби:

.

Применим табличный интеграл .

.

2)

Данный интеграл – также интеграл первого типа при . Эта задача отличается от предыдущей тем, что коэффициент, стоящий при в знаменателе, не равен единице. Для того, чтобы свести этот случай к предыдущему, этот коэффициент вынесем за скобку и затем выделим полный квадрат:

.

.

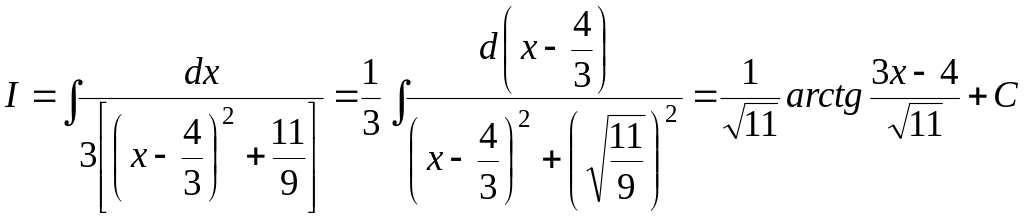3)

Данный интеграл – интеграл первого типа при . Выделим полный квадрат в знаменателе дроби:

.

Применим табличный интеграл .

.

4)

Данный интеграл – интеграл второго типа при .

Преобразуем дробь, стоящую под знаком интеграла. Выделим в числителе из производную знаменателя, равную , так, чтобы величина числителя при этом не изменилась:

.

Поэтому

Преобразуем получившийся интеграл в разность двух интегралов. Во втором интеграле в знаменателе выделим полный квадрат:

.

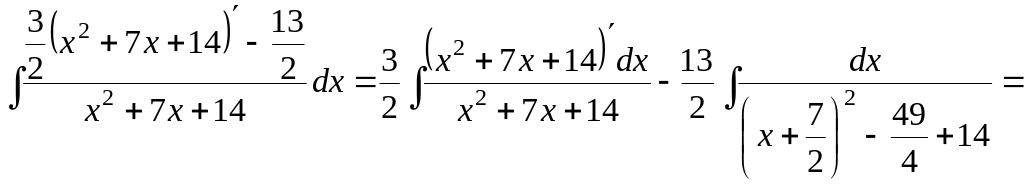
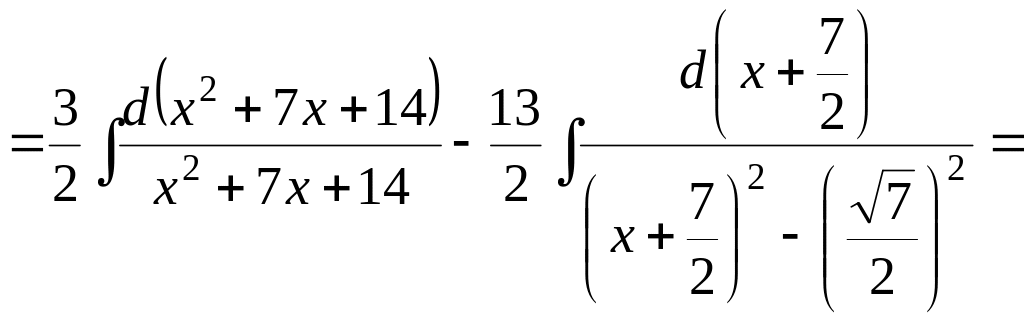
Замечание: Под знаком логарифма трехчлен не взят по абсолютной величине, так как его корни комплексные, коэффициент при положителен, а, значит, при любом этот трехчлен положителен.

5)

Данный интеграл – интеграл третьего типа. Вынесем из-под корня:

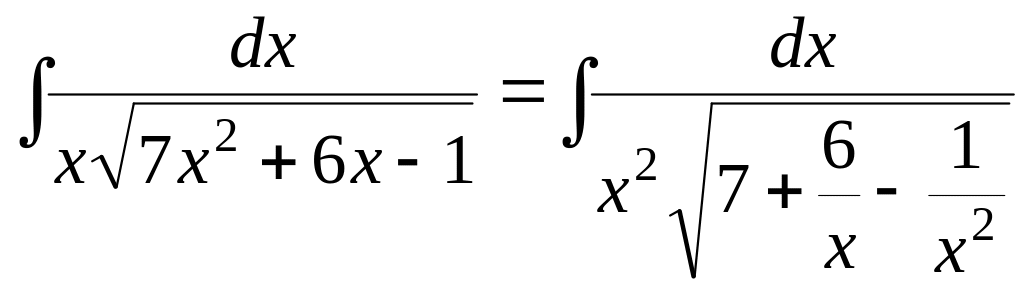
Преобразуем знаменатель:

.

Проведем операцию внесения под знак дифференциала:

.

Используя проведенные преобразования и табличный интеграл:

,

получим:

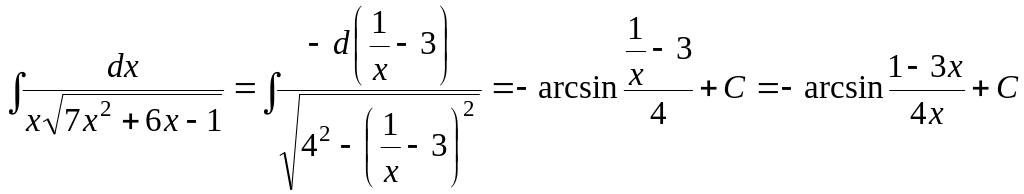
6) Рассмотрим пример на применение рекуррентной формулы.

Разобьем интеграл на два интеграла. К первому применим метод подведения под знак дифференциала, ко второму – рекуррентную формулу , положив в ней , и

.
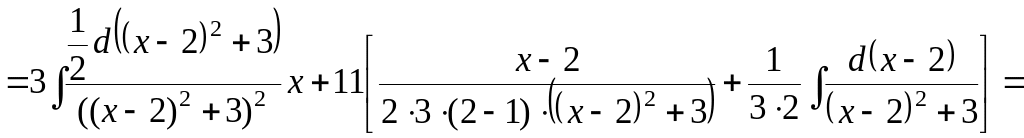