5.3 Метод замены переменных (способ подстановки)

Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, то есть перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной. Он основан на следующей теореме.

Теорема. Пусть функция определена и дифференцируема на некотором промежутке Т, и пусть Х – множество значений этой функции, на котором определена функция . Тогда, если на множестве Х функция имеет первообразную, то на множестве Т справедлива формула

.

Эта формула называется формулой замены переменных в неопределенном интеграле.

Доказательство: Продифференцируем предлагаемое равенство:

.

По свойству неопределенного интеграла: ,

что с учетом введенных обозначений и является исходным предположением. Теорема доказана.

Укажем два правила подстановки.

I правило подстановки основано на применении формулы

.

Здесь функция заменяется новой переменной .

Этот метод подробно рассмотрен как метод подведения под знак дифференциала в предыдущем параграфе.

II правило подстановки основано на применении формулы

.

Здесь, в отличие от предыдущего правила, сама независимая переменная заменяется новой функцией. То есть осуществляется операция «вывода функции из-под знака дифференциала».

Алгоритм его применения:

1) Независимую переменную заменяют удачно подобранной функцией по формуле:

. (3)

где — дифференцируемая функция.

Заметим, что функция в (3) должна иметь обратную. Это необходимо для того, чтобы из подстановки (3) можно было определить как функцию .

2) После этого определяют , а интеграл приводят к виду . Цель подстановки будет достигнута, если окажется, что вычисление этого интеграла проще, чем исходного.

3) Вычисляют получившийся интеграл. В результате интегрирования получится функция независимой переменной .

4) Результат выражают через первоначальную переменную . Чтобы возвратиться к переменной , надо из уравнения (3) определить через и подставить это значение вместо в найденную функцию.

Общего правила, которое указывало бы, как выбрать функцию в (3), не существует. Умение выбрать эту функцию достигается опытом. Однако для многих типов интегралов подстановка (3) известна.

Укажем некоторые рекомендации по выбору новой переменной:

а) если подынтегральная функция содержит , то бывает полезна тригонометрическая подстановка . При этом:

;

б) если подынтегральная функция содержит , то полезна замена . При этом:

.

в) если подынтегральная функция содержит , то полезна замена . При этом:

.

г) если подынтегральная функция содержит , то полезна замена . Такая подстановка позволяет рационализировать функцию (свести к рациональной).

.

Тогда

Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.

Примеры: вычислить интегралы.

1)

.

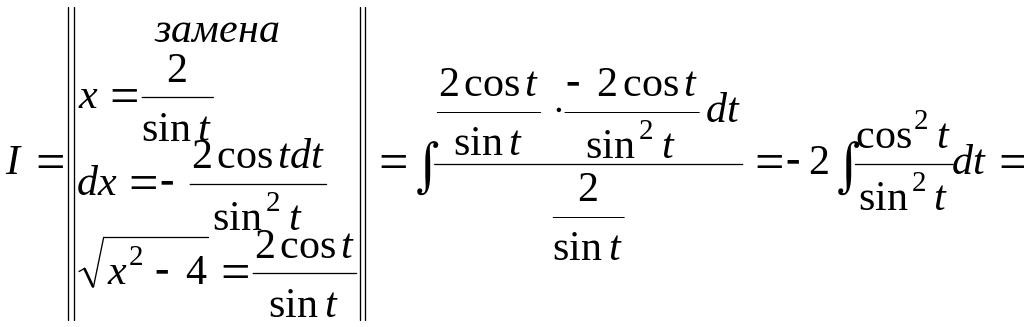
Вернемся к исходной переменной. Для этого выразим и через .

.

Поскольку ,

то и ,

откуда .

Таким образом,

.

2)

.

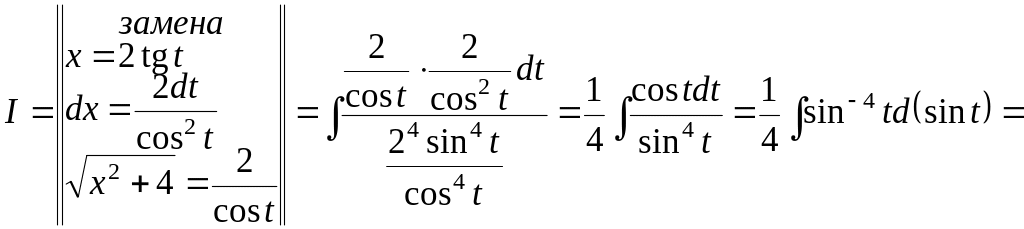
Выразим интеграл через исходную переменную, учитывая, что . Удобно воспользоваться прямоугольным треугольником с острым углом , противолежащим катетом и прилежащим катетом, равным (см. рис)

Из рисунка, гипотенуза данного треугольника равна , а . Тогда искомый интеграл равен:

.

3)

.

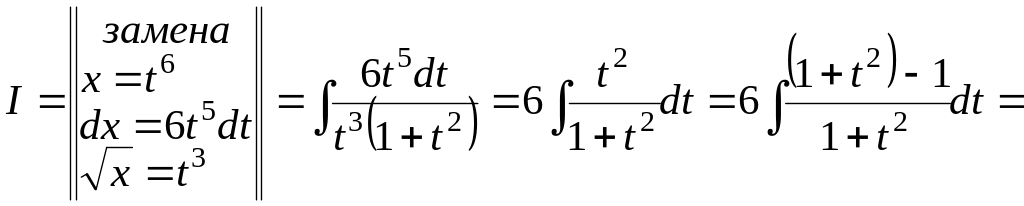
4)

.

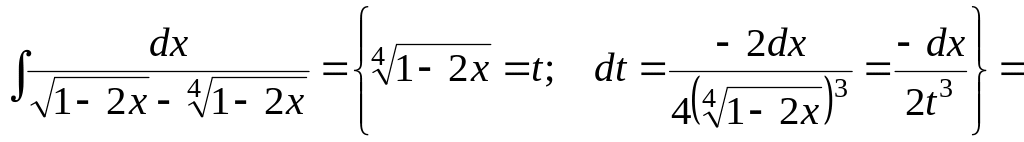
5)

.