4. Таблица основных интегралов

Во всех формулах под и понимается или независимая переменная, или произвольная функция любой независимой переменной, дифференцируемая в некотором промежутке.

Каждая из формул этой таблицы справедлива в любом промежутке, содержащемся в области определения соответствующей подынтегральной функции.

Интегралы, помещенные в таблице, называют табличными.

1		10
2		11
3		12
4		13
5		14
6		15
7		16
8		17
9		18

5. Методы интегрирования

5.1 Непосредственное интегрирование

Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием.

Рассмотрим применение этого метода на примерах.

1. Требуется найти значение интеграла . На основе известной формулы дифференцирования можно сделать вывод, что искомый интеграл равен , где С – некоторое постоянное число. Однако, с другой стороны . Таким образом, окончательно можно сделать вывод:

.

2. Вычислить интеграл .

Для вычисления интеграла следует разделить мно­гочлен, стоящий в числителе, на знаменатель. Если это выпол­нить, то получится, что

.

Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец, определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.

Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.

5.2 Метод подведения под знак дифференциала

Этот метод применяется для вычисления интегралов вида:

.

Воспользуемся тем, что . И перепишем интеграл в виде:

. (2)

При этом говорят, что мы подвели функцию под знак дифференциала.

Отметим, что при подведении функции под знак дифференциала прежде всего используется определение дифференциала:

или

и два его свойства:

и .

Рассмотрим, как подвести под знак дифференциала некоторые функции:

1) ,

Оговорка существенна, так как если , то , и тогда в правой части формулы знаменатель равен нулю. Когда , следует пользоваться формулой (4) Таблицы интегралов: .

2)

3)

4)

5)

6) .

Список таких формул можно продолжить. Важно понять, как они получаются.

Алгоритм применения метода подведения под знак дифференциала:

Все примеры этого параграфа решаются с помощью формулы (2):

.

Прежде, чем применить ее, надо выяснить: 1) какую из функций, стоящих под интегралом, следует принять равной и 2) есть ли под интегралом множитель, равный .

Примеры: вычислить интегралы.

1)

В этом примере подынтегральная функция равна . Примем, что . Тогда . Перепишем подынтегральную функцию в виде , отчего ее значение не изменится. При интегрировании постоянный множитель вынесем за знак интеграла и применим формулу (2) и табличный интеграл (3):

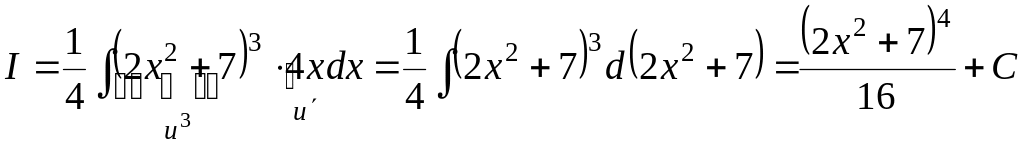
2) .

Примем, что . Тогда . Поэтому:

.

3) .

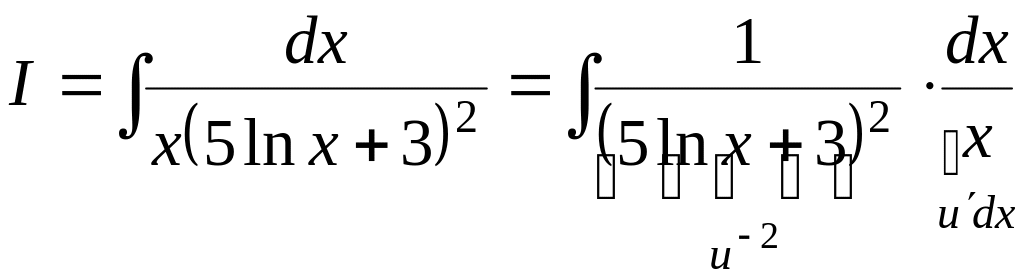Примем, что . Тогда . Воспользуемся правилом подведения под знак дифференциала:

.

Тогда:

.

4) .

Примем, что . Тогда . Значит, недостает множителя . Поэтому подынтегральную функцию представим в виде:

.

Тогда:

.

5) .

Примем, что . Тогда .

.