Оценка значимости коэффициентов полученной модели

Все численные значения коэффициентов модели случайные величины . Они имеют нормальный закон распределения.

,

где - генеральное математическое ожидание;

– генеральная дисперсия.

Для каждого из коэффициентов модели необходимо выяснить равно ли нулю генеральное математическое ожидание, если , такой коэффициент называется не значимым и в нашей модели он случайно отличается от нуля. Его надо убрать из модели и модель пересчитать снова без него.

Для каждого коэффициента первой и второй модели формируется нулевая гипотеза.

, т.е. или

Задаюсь уровнем ошибки первого рода .

Для проверки гипотезы применяется статистика Стьюдента (t-статистика)

,

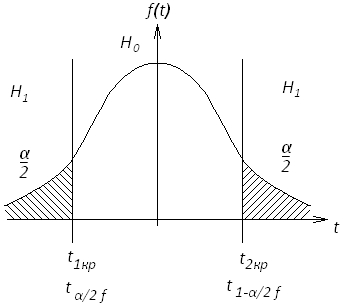
Так как всегда, то попасть в левую полуплоскость мы не можем. Поэтому сравниваем его только со 2 границей.

Если , то мы отвергаем нулевую гипотезу с вероятностью ошибки 5%. Значит у данного коэффициента генеральное математическое ожидание , т.е. коэффициент значим.

Если , то я принимаю нулевую гипотезу с вероятностью ошибки 5%. Коэффициент не значим, его нужно убрать из модели.

По таблице Стьюдента:

- число степеней свободы, где N - число опытов, L – число параметров

Для полной модели , t_кр1 = 2,11.

Для выборочной модели , t_кр2 = 2,10.

По полученным данным лабораторной работы мы уже имеем t-статистику для каждого из коэффициентов, поэтому мы сравниваем уже имеющиеся данные.

Оценка значимости коэффициентов (полная):

Номер	Коэф. модели	Т- Статистика
1	13,64	3,108
2	-2,721	0,6321
3	0,3846	0,06183
4	0,4896	0,1308
5	-3,915	1,842
6	-0,07087	0,009579

для 2,3,4,5,6 справедлива нулевая гипотеза эти коэффициенты не значимы, эти слагаемые из уравнения нужно удалить. Коэффициент 1, значим. Решение принимаю с вероятностью ошибки равной

Получаем вид модели:

Оценка значимости коэффициентов (выборочная):

Номер	Коэф. модели	Т- Статистика
1	14,87	11,02
2	-0,5633	0,5924
3	1,541	0,8613
4	1,059	0,9329
5	-0,0004651	0,0007566

для 2,3,4,5 справедлива нулевая гипотеза эти коэффициенты не значимы, эти слагаемые из уравнения нужно удалить. Коэффициент 1, значим. Решение принимаю с вероятностью ошибки равной

Получаем вид модели:

Оценка адекватности модели данного эксперимента

Оценка адекватности модели данным осуществляется путём сравнения точности модели относительно данных эксперимента и точности экспериментальных данных по параллельным опытам.

Точность экспериментальных данных одна и та же ,

Необходимо определить точность модели , .

,

где N – число опытов;

– число параметров, которые рассчитываются в данной модели.

Для полной модели:

Для выборочной модели:

Значения остаточной дисперсии для каждой модели известны из расчетных данных:

Для полной модели:

Для выборочной модели: .

Полагаю, что генеральная дисперсия модели , а генеральная дисперсия экспериментальных данных .

Выдвигается нулевая гипотеза : полагается, что модель адекватна данным эксперимента, т.е. они имеют общую генеральную дисперсию . Альтернативная гипотеза .

Задаемся уровнем ошибки первого рода

Для проверки такой нулевой гипотезы воспользуемся критерием Фишера с статистикой, которая зависит от и двух некоторых показателей степеней свободы и . Причём всегда .

Здесь , .

Для полной модели:

По таблице Фишера нахожу критическое значение: .

Кривая распределения Фишера.

Так как , следовательно, я отвергаю нулевую гипотезу и принимаю альтернативную гипотезу с вероятностью ошибки 5%. Это означает, что модель не адекватна данным эксперимента, необходимо изменить структуру модели.

Для выборочной модели:

По таблице Фишера нахожу критическое значение: .

Кривая распределения Фишера.

Так как , следовательно, я отвергаю нулевую гипотезу и принимаю альтернативную гипотезу с вероятностью ошибки 5%.

Так как , следовательно, я отвергаю нулевую гипотезу и принимаю альтернативную гипотезу с вероятностью ошибки 5%. Это означает, что модель не адекватна данным эксперимента, необходимо изменить структуру модели.

Данная модель также не адекватна данным эксперимента. Необходимы следующие дальнейшие варианты работы:

1. изменить структуру модели;

2. если это не поможет, то увеличить число экспериментальных данных (снова провести опыт);

3. добавить новый фактор (еще один входной сигнал).

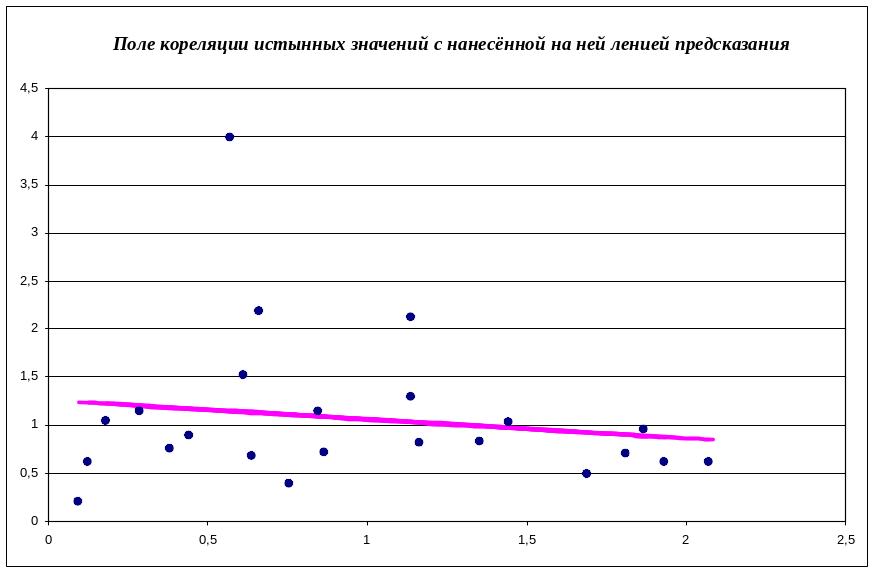
4.2 Корреляционный анализ включает в себя

- оценку независимых входных переменных по программно рассчитанной матрице и по виду поля корреляции

- оценку зависимости коэффициентов модели при принятии вывода об удалении определённого коэффициента в силу его незначимости.

- оценку независимости ошибок модели относительно данных эксперимента по виду корреляционной функции ошибки.

Уравнение линии предсказания:

,

Значение берётся из матрицы входных переменных

и получаем линию предсказания.

Вывод:

- По виду поля корреляции можно сделать вывод, об отсутствии какой либо связи.

- По положению линии корреляции можно сказать что Х₂ уменьшается - это значит, что корреляция отрицательная.

№ модели	Вид модели	Коэффициент модели						Критерий Стьюдента		Точность эксперимента		Точность модели		Критерий Фишера		Вывод
		Т - статистика
		b1	b2	b3	b4	b5	b6	fi	tкр	σ2ост	fвосп	σост	fост	Fрас	F1-a,f
		tb1	tb2	tb3	tb4	tb5	tb6
1	Y1=13,64	13,64	-2,721	0,3846	0,4896	-3,915	-0,07087	17	2,11	0,205	2	177,9	17	8,56	161,4	Модель не адекватна
		3,108	0,6321	0,06183	0,1308	1,842	0,009579
		значим	не значим	не значим	не значим	не значим	не значим
2	Y2=14,87	14,87	-0,5633	1,541	1,059	-0,0004651		18	2,1	0,205	2	16,85	18	8,56	161,4	Модель не адекватна
		11,02	0,5924	0,8613	0,9329	0,0007566
		значим	не значим	не значим	не значим	не значим	не значим