Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

«Санкт – Петербургский государственный технологический

Университет растительных полимеров»

Кафедра автоматизации технологических процессов и производств

Отчет по пассивному эксперименту

Вариант 97

По дисциплине: Моделирование систем

Выполнил: ст. гр. 542 Пермин Д.С.

Проверил: Селянинова Л.Н.

Санкт – Петербург

2012 г.

1. Блочная схема объекта с обозначением входных и выходных переменных(факторов). Результаты пассивного эксперимента.

Результаты независимых измерений – исходные данные

№ эксп.	Х1	Х2	У1
1	1,552	0,879	16,197
2	0,572	3,981	13,745
3	1,692	0,484	16,573
4	1,811	0,704	17,186
5	1,166	0,816	14,546
6	0,848	1,137	13,385
7	0,183	1,042	10,545
8	1,138	2,122	15,124
9	2,071	0,616	18,233
10	0,444	0,885	11,558
11	0,123	0,618	10,069
12	0,614	1,513	12,605
13	1,869	0,95	17,563
14	1,137	1,292	14,679
15	0,66	2,181	13,154
16	0,289	1,14	11,044
17	1,354	0,83	15,339
18	0,756	0,394	12,6
19	0,865	0,71	13,227
20	0,64	0,673	12,263
21	1,217	0,966	14,84
22	0,383	0,756	14,84
23	1,931	0,615	17,642
24	1,445	1,028	15,826
25	0,093	0,199	9,718

Пассивный эксперимент основан на регистрации контролируемых переменных в установившемся режиме работы.

Объект с указанием всех переменных:

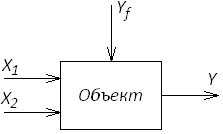
входные переменные;

выходная переменная, зависит от , ;

возмущающие входные факторы.

Статическая модель объекта устанавливает соответствие между входными и выходными переменными объекта в установившемся режиме.

2. Статистический анализ результатов пассивного эксперимента.

2.1 Формирование экспериментов из параллельных исходных данных.

Пассивный эксперимент основан на регистрации контролируемых переменных в установившемся режиме работы ( . Регистрация происходит через длительные моменты времени, чтобы не было взаимного влияния измерений друг на друга.

Результаты первого эксперимента:

1,552	0,879	16,197
1,354	0,830	15,339

Результаты второго эксперимента:

1,166	0,816	14,546
1,217	0,966	14,840

где – число параллельных опытов в первом эксперименте;

– число степеней свободы;

– число параллельных опытов во втором эксперименте;

– число степеней свободы;

Для каждого эксперимента необходимо рассчитать и , как оценку точности. Для обработки данных необходимо из каждого эксперимента учитывать только один выделенный опыт, поэтому из исходных данных нужно убрать по 1-му измерению из каждого опыта.

2. Расчет выборочных оценок математического ожидания и дисперсии для сформированных выборок.

Выборочное математическое ожидание:

Выборочная дисперсия:

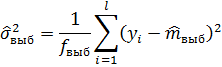
Для первого эксперимента:

Для второго эксперимента:

2.3 Оценка однородности выборочных дисперсий.

При проведении параллельных опытов необходимо определить являются ли результаты измерений в первом и во втором эксперименте статистически одинаковыми (т.е. принадлежат ли эти все измерения одной генеральной совокупности, а именно имеют одни и те же генеральные параметры).

Допустим, что первый эксперимент характеризуется генеральным значением , второй - .

Выдвигается нулевая гипотеза : полагается, что обе выборки принадлежат одной и той же генеральной совокупности, т.е. у них одно и то же значение генеральной дисперсии . А выборочные дисперсии – это случайные оценки этой генеральной дисперсии; , поэтому выдвигается альтернативная гипотеза

Задаемся уровнем ошибки первого рода .

Для проверки такой нулевой гипотезы используется статистика Фишера , которая зависит от и двух некоторых показателей степеней свободы и . Причём всегда .

Кривая распределения Фишера.

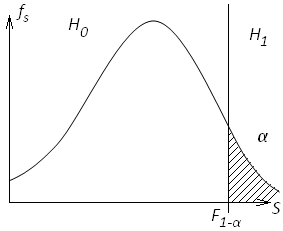
Проверить нулевую гипотезу, означает найти одну границу. Для этого надо найти расчётное значение и посмотреть в какую область попадём.

По таблице Фишера нахожу значение .

Получаю, что , Верна нулевая гипотеза, выборочные оценки дисперсии статистически однородны их различие статистически не значимо, эти дисперсии могут иметь одну и ту же генеральную дисперсию с вероятностью ошибки 5%. И первый и второй эксперимент соответствуют одним и тем же условиям проведения опыта. Тогда из каждого параллельного опыта оставляем по одному опыту.

2.4 Объём экспериментальных данных с учётом результата оценки однородности выборочных дисперсий параллельных опытов

№ эксп.	Х1	Х2	У1
1	0,572	3,981	13,745
2	1,692	0,484	16,573
3	1,811	0,704	17,186
4	1,166	0,816	14,546
5	0,848	1,137	13,385
6	0,183	1,042	10,545
7	1,138	2,122	15,124
8	2,071	0,616	18,233
9	0,444	0,885	11,558
10	0,123	0,618	10,069
11	0,614	1,513	12,605
12	1,869	0,95	17,563
13	1,137	1,292	14,679
14	0,66	2,181	13,154
15	0,289	1,14	11,044
16	1,354	0,83	15,339
17	0,756	0,394	12,6
18	0,865	0,71	13,227
19	0,64	0,673	12,263
20	0,383	0,756	14,84
21	1,931	0,615	17,642
22	1,445	1,028	15,826
23	0,093	0,199	9,718

При условии статистически однородных опытов находится общая оценка экспериментальных данных в виде дисперсии воспроизводимости.

2.5 Оценка точности сформированного объема экспериментальных данных, расчёт дисперсии воспроизводимости данных и числа её степеней свободы

3. Расчёт двух структур моделей статистики (полной и выборочной) по сформированному объёму экспериментальных данных, представлен в приложении.

4. Статический анализ рассчитанных моделей.

4.1 Регрессионный анализ каждой модели включает в себя

- оценку значимости каждого коэффициента модели;

- оценку адекватности модели.