Центральная предельная теорема

Многие непрерывные случайные величины имеют нормальное распределение. Это обстоятельство во многом определяется тем, что суммирование большого числа случайных величин с самыми разными законами распределения приводит к нормальному распределению этой суммы.

Указанное свойство подтверждается интегральной предельной теоремой, доказанной Ляпуновым.

Теорема. Если случайная величина представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.

Центральная предельная теорема имеет огромное значение для практики.

Допустим, определяется некоторый экономический показатель, например, потребление электроэнергии в городе за год. Величина суммарного потребления складывается из потребления энергии отдельными потребителями, которая имеет случайные значения с разными распределениями. Теорема утверждает, что в этом случае, какое бы распределение не имели отдельные составляющие, распределение результирующего потребления будет близко к нормальному.

Однако следует иметь в виду, что при усилении влияния отдельных факторов могут появляться отклонения от нормального распределения результирующего параметра, например, может возникнуть асимметрия или эксцесс. Поэтому большое значение на практике уделяется экспериментальной проверке выдвинутых гипотез, в том числе и гипотезы о нормальном распределении.

Поэтому, в некоторых случаях приходится рассматривать распределение случайной величины, имеющие определенные отличия от нормального. Для оценки этого отличия введены специальные характеристики. К ним относятся, в частности, асимметрия и эксцесс.

Асимметрией распределения случайной величины называется отношение центрального момента третьего порядка к кубу среднего квадратичного отклонения:

.

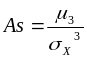Эксцессом распределения случайной величины называют число, определяемое выражением:

.

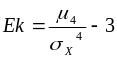Для нормального распределения 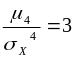, поэтому эксцесс равен нулю.

Вероятность попадания нормальной случайной величины в заданный интервал

Во многих практических задачах требуется определить вероятность попадания случайной величины в заданный интервал. Эта вероятность может быть выражена в виде разности функции распределения вероятности в граничных точках этого интервала:

.

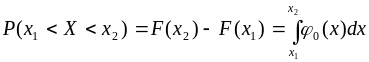В случае нормального распределения:

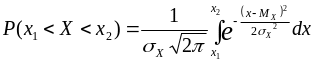
сделаем замену переменной: , , .

Тогда:

,

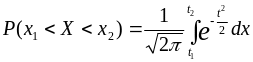где , .

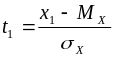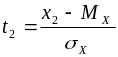Разобьем полученный интеграл на два:

.

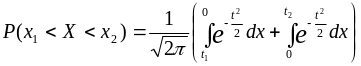
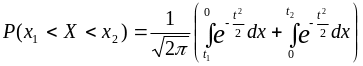
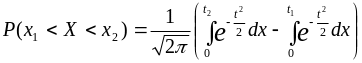Следовательно, искомая вероятность может быть выражена через веденный ранее стандартный интеграл Лапласа:

.

Функция Лапласа и ее свойства

Функция Лапласа не выражается через элементарные функции

.

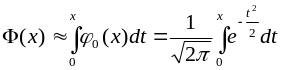Для ее вычисления используются специальные таблицы или методы приближенного вычисления.

Функция обладает следующими свойствами:

1. ;

2. ;

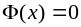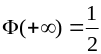3. функция – нечетная, т.е. = – , поэтому в таблицах обычно приводятся значения только для положительных ;

4. функция – монотонно возрастающая функция (это следует из того, что 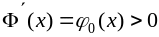). При , с точностью до тысячных можно принять .