Начальные и центральные моменты

Кроме математического ожидания и дисперсии, для оценки случайной величины используются начальные и центральные моменты случайной величины. Начальным моментом порядка случайной величины называют математическое ожидание величины :

.

Центральным моментом порядка случайной величины называют математическое ожидание величины :

.

Начальный момент первого порядка равен математическому ожиданию самой случайной величины .

Центральный момент первого порядка равен нулю:

.

Центральный момент второго порядка представляет собой дисперсию случайной величины :

.

Для дискретных случайных величин:

;

.

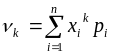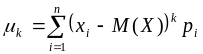Основные примеры распределений дискретной случайной величины

Случайную величину полностью задает закон ее распределения. Чтобы определить закон распределения дискретной случайной величины, необходимо установить соответствие между всеми возможными значениями данной случайной величины и их вероятностями.

К каноническим законам распределения дискретной случайной величины обычно относят биномиальный закон, закон распределения Пуассона и закон распределения по геометрической прогрессии.

Биномиальное распределение, его математическое ожидание, дисперсия

Рассмотрим серию независимых испытаний проведенных в условиях схемы Бернулли, в ходе которых появлялось событие с вероятностью , одинаковой для всех испытаний.

Необходимо определить закон распределения случайной величины числа появлений события . Для этого нужно определить возможные значения и их вероятности. Минимальное значение равно нулю, что соответствует ситуации, когда в серии испытаний событие не появилось; максимальное значение соответствует «успеху» во всех испытаниях серии и равно . Очевидно, что случайная величина числа появлений события в серии испытаний принимает значения . Остается найти соответствующие вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:

,

где , .

Эта формула является аналитическим выражением искомого закона распределения. Эта формула еще называется биномиальной, так как ее правая часть представляет собой -й член бинома Ньютона:

.

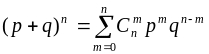Отсюда сразу видно, что для полученного закона биномиального распределения вероятностей числа появления события при независимых испытаниях выполняется условие нормировки, т.е. сумма всех вероятностей равна единице:

.

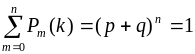Теорема. Математическое ожидание числа появлений события в независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.

Доказательство. Случайная величина распределена по биномиальному закону:

( ),

где .

Величину можно рассматривать, как сумму независимых случайных величин , где ( ) – число появлений события в м испытании. Случайная величина принимает лишь два значения: 1, если событие появилось в м испытании, и 0, если в м испытании события не произошло.

Вероятности этих событий и , а математическое ожидание: ( ).

Следовательно, используя теорему о математическом ожидании суммы, получим:

.

Таким образом, математическое ожидание числа появлений события в условиях схемы Бернулли совпадает со средним числом появлений события в данной серии испытаний.

Теорема. Дисперсия числа появлений события в независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: .

Доказательство. Пусть – число появлений события в независимых испытаниях. Оно равно сумме появлений события в каждом испытании: . Так как испытания независимы, то и случайные величины – независимы, поэтому .

Но , .

Как было показано выше, , а .

Тогда , а .

В этом случае, как уже упоминалось ранее, среднее квадратичное отклонение .

Пример. В пяти торговых точках проверяется годовой баланс. Вероятность правильного оформления баланса в каждой точке равна 0,7. Найти математическое ожидание и дисперсию правильно оформленных балансов.

Решение. Дано: , , .

Тогда

.

Биномиальный закон распределения часть приходится применять в условиях, когда число независимых испытаний велико. Вычисление вероятностей по формуле Бернулли при этом усложняется, поэтому представляет интерес асимптотическое приближение для биномиального закона, справедливое при больших . Возможны два случая:

1. Когда при увеличении числа испытаний математическое ожидание рассматриваемой случайной величины тоже неограниченно возрастает (случай постоянного ); при этом биномиальное распределение сходится к нормальному закону, который будет рассмотрен позже.

2. Когда при увеличении числа испытаний остается постоянным произведение , то есть математическое ожидание рассматриваемой случайной величины остается конечным. Это означает, что вероятность события стремится к нулю. В этом случае биномиальное распределение сходится к распределению Пуассона.