Закон
полного тока это
закон, связывающий циркуляцию вектора
напряженности магнитного поля и ток.
Циркуляция
вектора напряженности магнитного поля
по контуру равна алгебраической сумме
токов, охватываемых этим контуром.
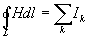
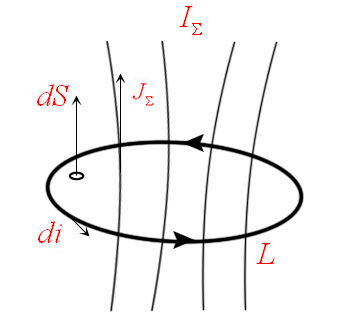
Положительным
считается ток, направление которого
связано с направлением обхода по контуру
правилом правого винта; ток протоивоположного
направления считается отрицательным.
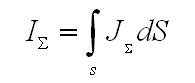 Соленоид
можно представить в виде системы
одинаковых круговых
токов с общей прямой
осью.
Соленоид
можно представить в виде системы
одинаковых круговых
токов с общей прямой
осью.
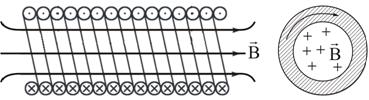
Бесконечно
длинный соленоид симметричен любой,
перпендикулярной к его оси плоскости.
Взятые попарно (рис. 2.12), симметричные
относительно такой плоскости витки
создают поле, в котором вектор 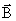 перпендикулярен
плоскости витка, т.е. линии
магнитной индукции имеют
направление параллельное оси
соленоида внутри
и вне его.
перпендикулярен
плоскости витка, т.е. линии
магнитной индукции имеют
направление параллельное оси
соленоида внутри
и вне его.
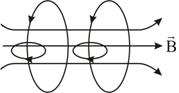
Поле
как внутри, так и вне соленоида должно
быть однородным.
Тогда
магнитная индукция внутри
соленоида: 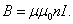
Вне
соленоида:
 и
и
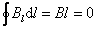 т.е
т.е
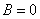
9
Намагничивание
вещества. Намагниченность. Магнитная
восприимчивость
Магнитная
восприимчивость — физическая
величина,
характеризующая связь между магнитным
моментом(намагниченностью)
вещества и магнитным
полем в
этом веществе.
Магнитная
восприимчивость определяется
отношением намагниченности единицы
объёма вещества к напряжённости
намагничивающего магнитного поля.
По своему смыслу восприимчивость
является величиной
безразмерной.
Намагни́ченность — векторная физическая
величина, характеризующая магнитное состояние
макроскопического физического тела.
Обозначается обычно М или J.
Определяется как магнитный
момент единицы объёма вещества:
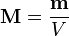
Здесь, M —
вектор намагниченности; m вектор
магнитного момента; V — объём.
[
В общем случае (случае неоднородной,
по тем или иным причинам, среды)
намагниченность выражается как
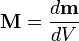
и
является функцией координат.]
Связь
между M и напряженностью
магнитного
поля H в диамагнитных и парамагнитных материалах
-
линейная
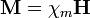
где χm называют магнитной
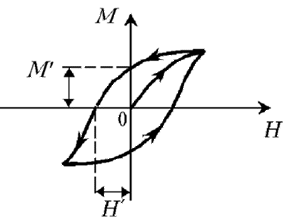
восприимчивостью. В ферромагнитных
материалах нет однозначной связи
между M и H из-замагнитного
гистерезиса.
Магнитная
индукция определяется через
намагниченность как:
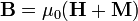 (в
системе СИ)
(в
системе СИ)
Намагничивание
вещества,
как уже было сказано, обусловлено
преимущественной ориентацией или
индуцированием магнитных моментов
отдельных молекул в одном направлении.
Намагничивание
вещества
происходит в направлении, противоположном
магнитной силе, [или, другими словами,
вещество является диамагнитным.]
Взаимодействие
магнитных моментов атомов и молекул с
внешним магнитным полем вызывает
намагничивание
веществ.
В
зависимости от характера этого
взаимодействия различают парамагнетики,
диамагнетики и ферромагнетики. Атомы
и молекулы парамагнетиков обладают
постоянным отличным от нуля магнитным
моментом. Во внешнем поле магнитные
моменты частиц ориентируются
преимущественно вдоль поля
10
Классификация магнетиков. Природа и
механизмы намагничивания.
Магнетики —
материалы, вступающие во взаимодействие
с магнитным полем, выражающееся в его
изменении, а также в других физических
явлениях — изменение физических
размеров, температуры, проводимости,
возникновению электрического потенциала
и т. д. К магнетикам относятся
практически все вещества, большинство
из них относится к классам
диамагнетиков (имеющие
небольшую отрицательную магнитную
восприимчивость — и несколько
ослабляющие магнитное поле)
или парамагнетиков (имеющие
небольшую положительную магнитную
восприимчивость — и несколько
усиливающие магнитное поле); более
редко встречаются ферромагнетики (имеющие
большую положительную магнитную
восприимчивость — и намного
усиливающие магнитное поле),
Диамагнетики -
это вещества, намагничивающиеся во
внешнем магнитном поле против направления
поля. (Например Ag, Au, Cu)
Диамагнитный
эффект - это эффект, при котором
составляющие магнитных полей атомов
складываются и образуют собственное
магнитное поле вещества, ослабляющее
внешнее магнитное поле.
Так
как диамагнитный эффект обусловлен
действием внешнего магнитного поля на
электроны атомов вещества, то диамагнетизм
свойствен всем веществам.
Парамагнетики -
это вещества, намагничивающиеся во
внешнем магнитном поле по направлению
поля (например редкоземельные металлы,
Pt, Al).
У парамагнетиков при
отсутствии внешнего магнитного поля
магнитные моменты электронов не
компенсируют друг друга, и молекулы
парамагнетиков всегда
обладают магнитным моментом (такие
молекулы называются полярными).
Вследствие
теплового движения молекул их магнитные
моменты ориентированы беспорядочно,
поэтому в отсутствие магнитного
поля,парамагнетики магнитными
свойствами не обладают.
При
внесении парамагнетика во
внешнее магнитное поле устанавливается
преимущественная ориентация магнитных
моментов атомов (молекул) по полю (полной
ориентации препятствует тепловое
движение атомов).
Ферромагнетики -
это вещества, обладающие спонтанной
намагниченностью, то есть они сохраняют
намагниченность при отсутствии внешнего
магнитного поля.
К ферромагнетикам относятся,
например, кристаллы железа, никеля,
кобольта.
Ферромагнитные
свойства вещества существенно зависят
от температуры. С повышением температуры
остаточная намагниченность ферромагнетика
уменьшается.
При достаточно высокой температуре,
называемой точкой Кюри, она исчезает
полностью. При нагревании выше точки
Кюри ферромагнетик превращается
в обычный парамагнетик.
11
Явление электромагнитной индукции.
Закон Фарадея. Правило Ленца. Самоиндукция.
ЭДС индукции
Электромагнитная
индукция —
явление возникновения электрического
тока в
замкнутом контуре при изменении магнитного
потока,
проходящего через него.
Электрический
ток,
вызванный этой ЭДС, называется
индукционным током.
[
Согласно закону электромагнитной
индукции Фарадея (в СИ):
где
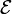 — электродвижущая
сила, действующая вдоль произвольно
выбранного контура,
— электродвижущая
сила, действующая вдоль произвольно
выбранного контура,
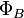 — магнитный
поток через поверхность, натянутую
на этот контур.
— магнитный
поток через поверхность, натянутую
на этот контур.
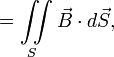 ]
Знак
«минус» в формуле отражает правило
Ленца,
]
Знак
«минус» в формуле отражает правило
Ленца,
Индукционный
ток, возникающий в замкнутом проводящем
контуре, имеет такое направление, что
создаваемое им магнитное поле
противодействует тому изменению
магнитного потока, которым был вызван
данный ток.
[Для
катушки, находящейся в переменном
магнитном поле, закон Фарадея можно
записать следующим образом:
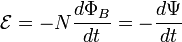
где
—
электродвижущая
сила,
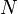 —
число
витков,
—
число
витков,
—
магнитный
поток через один виток,
Самоиндукция —
возникновение ЭДС индукции в
замкнутом проводящем контуре[1] при
изменении тока,
протекающего по контуру.
При
изменении тока в контуре пропорционально
меняется[2] и магнитный
поток через поверхность,
ограниченную этим контуром[3].
Изменение этого магнитного потока, в
силу закона
электромагнитной индукции, приводит
к возбуждению в этом контуре
индуктивной ЭДС.
Направление
ЭДС самоиндукции всегда оказывается
таким, что при возрастании тока в цепи
ЭДС самоиндукции препятствует этому
возрастанию (направлена против тока),
а при убывании тока — убыванию
(сонаправлена с током). Этим свойством
ЭДС самоиндукции сходна с силой
инерции.
Величина
ЭДС самоиндукции пропорциональна
скорости изменения силы тока 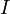 :
:
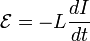 .
.
Коэффициент
пропорциональности 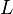 называется коэффициентом
самоиндукции или индуктивностью контура
(катушки).
называется коэффициентом
самоиндукции или индуктивностью контура
(катушки).
12
Индуктивность. Взаимная индукция.
Индуктивность соленоида.
Индукти́вность (или коэффициент
самоиндукции) —
коэффициент пропорциональности между
электрическим током,
текущим в каком-либо замкнутом контуре,
и магнитным
потоком, создаваемым этим током через
поверхность[1],
краем которой является этот
контур.[2][3][4].
В
формуле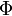 —
магнитный поток,
—
ток в контуре,
—
индуктивность.
—
магнитный поток,
—
ток в контуре,
—
индуктивность.
Через
индуктивность выражается ЭДС
самоиндукции в контуре, возникающая
при изменении в нём тока[4]:
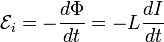 .
.
Из
этой формулы следует, что индуктивность
численно равна ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1 А за 1 с.
[Практически
участки цепи со значительной индуктивностью
выполняют в виде катушек
индуктивности[4].]
При
заданной силе тока индуктивность
определяет энергию магнитного
поля тока[4]:
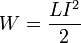 .
.
Взаимоиндукция
(взаимная индукция) —
возникновение электродвижущей силы
(ЭДС)
в одном проводнике вследствие
изменения силы
тока в
другом проводнике или вследствие
изменения взаимного расположения
проводников. Взаимоиндукция —
частный случай более общего
явления — электромагнитной
индукции.
При изменении тока в одном из проводников
или при изменении взаимного расположения
проводников происходит изменение магнитного
потока
через
поверхность, "натянутую" на контур
второго, созданного магнитным полем,
порожденным током в первом проводнике,
по закону
электромагнитной индукции вызывает
возникновение ЭДС во втором проводнике.
Если второй проводник замкнут, то под
действием ЭДС взаимоиндукции в нём
образуется индуцированный ток. И
наоборот, изменение тока во второй цепи
вызовет появление ЭДС в первой.
Направление тока, возникшего при
взаимоиндукции, определяется по правилу
Ленца.
Соленоид —
длинная, тонкая катушка, то есть катушка,
длина которой намного больше, чем её
диаметр (толщина обмотки намного меньше,
чем диаметр катушки). При этих условиях
и без использования магнитного материала
плотность магнитного потока 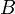 внутри
катушки является фактически постоянной
и (приближенно) равна
внутри
катушки является фактически постоянной
и (приближенно) равна
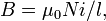
где 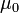 − магнитная
постоянная,
−
число витков,
− магнитная
постоянная,
−
число витков, 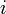 −
ток и
−
ток и 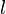 −
длина катушки. Пренебрегая краевыми
эффектами на концах соленоида,
получим[10],
что потокосцепление через катушку
равно плотности потока
,
умноженному на площадь поперечного
сечения
−
длина катушки. Пренебрегая краевыми
эффектами на концах соленоида,
получим[10],
что потокосцепление через катушку
равно плотности потока
,
умноженному на площадь поперечного
сечения 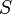 и
число витков
:
и
число витков
:
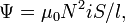
Отсюда
следует формула
для индуктивности соленоида (без
сердечника):
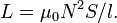
Если
катушка внутри полностью заполнена
магнитным материалом (сердечником),
то индуктивность отличается на
множитель 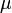 — относительную
магнитную проницаемость[11] сердечника:
— относительную
магнитную проницаемость[11] сердечника:
13
Энергия электрического поля. Энергия
и плотность энергии магнитного поля
Энергия Wе конденсатора
емкости C,
заряженного зарядом Q,
может быть найдена путем интегрирования
этого выражения в пределах от 0 до Q:
Формулу,
выражающую энергию заряженного
конденсатора, можно переписать в другой
эквивалентной форме, если воспользоваться
соотношением Q = CU.
Электрическую
энергию Wе следует
рассматривать как потенциальную
энергию, запасенную в заряженном
конденсаторе.
По
современным представлениям, электрическая
энергия конденсатора локализована в
пространстве между обкладками
конденсатора, то есть в электрическом
поле. Поэтому ее называют энергией
электрического поля. Это легко
проиллюстрировать на примере заряженного
плоского конденсатора.
Напряженность однородного
поля в плоском конденсаторе равна E = U/d,
а его емкость 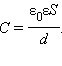 Поэтому
Поэтому
где V = Sd –
объем пространства между обкладками,
занятый электрическим полем. Из этого
соотношения следует, что физическая
величина
является
электрической (потенциальной) энергией
единицы объема пространства, в котором
создано электрическое поле. Ее
называют объемной
плотностью электрической энергии.
Энергия
поля, созданного любым распределением
электрических зарядов в пространстве,
может быть найдена путем интегрирования
объемной плотности wе по
всему объему, в котором создано
электрическое поле.
14
Вихревое
электрическое поле. Ток смещения.
Система уравнений Максвелла в интегральной
форме
Причина
возникновения электрического тока в
неподвижном проводнике - электрическое
поле.
Всякое изменение магнитного
поля порождает индукционное электрическое
поле независимо от наличия или отсутствия
замкнутого контура, при этом если
проводник разомкнут, то на его концах
возникает разность потенциалов; если
проводник замкнут, то в нем наблюдается
индукционный ток.
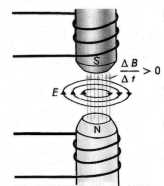 Индукционное
электрическое поле является
вихревым.
Направление силовых
линий вихревого эл. поля совпадает с
направлением индукционного
тока
Индукционное электрическое
поле имеет совершенно другие свойства
в отличии от электростатического поля.
Индукционное
электрическое поле является
вихревым.
Направление силовых
линий вихревого эл. поля совпадает с
направлением индукционного
тока
Индукционное электрическое
поле имеет совершенно другие свойства
в отличии от электростатического поля.
электростатическое
поле
|
индукционное
электрическое поле
( вихревое
электр. поле )
|
1.
создается неподвижными электр.
зарядами
|
1.
вызывается изменениями магнитного
поля
|
2.
силовые линии поля разомкнуты -
-потенциальное поле
|
2.
силовые линии замкнуты -
- вихревое
поле
|
3.
источниками поля являются электр.
заряды
|
3.
источники поля указать нельзя
|
4.
работа сил поля по перемещению пробного
заряда по замкнутому пути = 0.
|
4.
работа сил поля по перемещению пробного
заряда по замкнутому пути = ЭДС индукции
|
Интегральная
форма
Ток
смещения
—
величина, прямо пропорциональная
быстроте изменения электрической
индукции.
В
вакууме, а также в любом веществе, в
котором можно пренебречь поляризацией
либо скоростью её изменения, током
смещения
(с
точностью до универсального постоянного
коэффициента) называется[3] поток
вектора быстроты изменения электрического
поля 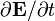 через
некоторую поверхность[4]
через
некоторую поверхность[4]  :
: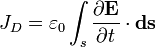
15. Гармонические колебания. Характеристики гармонических колебаний и их физический смысл.
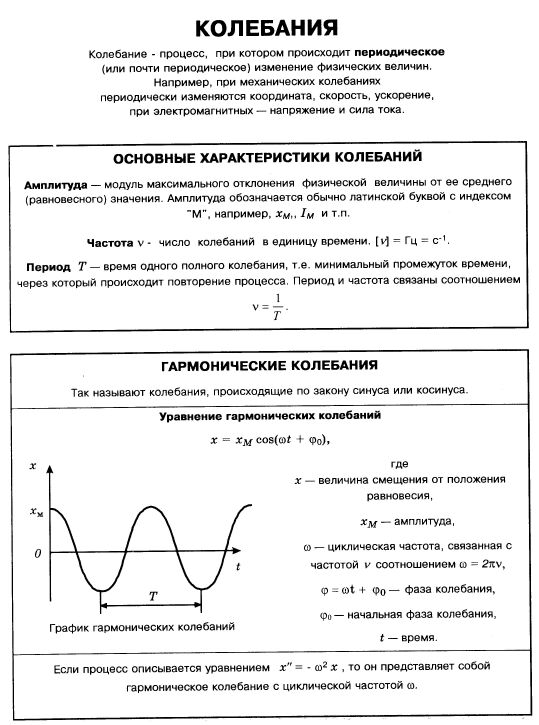
Гармонические
колебания – колебания, при которых
колеблющаяся величина изменяется со
временем по закону синуса или косинуса.
Колебания
встречающиеся в природе и технике
близки к гармоническим
Различные
периодические процессы можно представить
как наложение гармонических колебаний
x=A
cos
(ω0t
+ φ)
A
– максимальное значение колеблющейся
величины (амплитуда)
(х
принимает значения от +А до -А)
ω0
– круговая (циклическая) частота ( )
)
(ω0t
+ φ)-
фаза колебания. Она определяет смещение
колеблющейся величины от положения
равновесия в данный момент времени t.
φ
- начальная фаза. Она определяет смещение
колеблющейся величины от положения
равновесия в начальный момент времени
t=0.
Период
колебаний
(Т) – время, за которое происходит одно
полное колебание.
За
период фаза колебания получает приращение
2π.
ω0(t
+T)
φ=
(ω0t
+ φ)+2π
откуда 
Частота
колебаний
(ν) – Число полных колебаний. Совершаемых
в единицу времени. (величина обратная
периоду  )
[ν]=Гц
)
[ν]=Гц
Комплексная форма представления гармонических колебаний. Представление гармонических колебаний в векторной форме.
s=A
cos
(ω0t
+ φ)
Найдем
первую и вторую производные по времени
от величины s, совершающей гармонические
колебания:


Из
выражения (1) непосредственно вытекает
дифференциальное уравнение гармонических
колебаний

Гармонические
колебания графически изображаются
методом векторных диаграмм. Для этого
из произвольной точки О, которая выбрана
на оси х, под углом φ, который равен
начальной фазе колебания, откладывается
вектор А, у которого модуль равен
амплитуде А рассматриваемого колебания.
Если данный вектор привести во вращение
с угловой скоростью ω0, которая равна
циклической частоте колебаний, то
проекция конца вектора будет перемещаться
по оси х и принимать значения от –А до
+А, а колеблющаяся величина будет
изменяться со временем по закону s =
Acos(ω0t+φ).
Значит, гармоническое колебание можно
представить как проекцию на некоторую
выбранную произвольным образом ось
вектора амплитуды А, который отложен
из произвольной точки оси под углом φ
, равным начальной фазе, и вращающегося
с угловой скоростью ω0
вокруг этой точки.
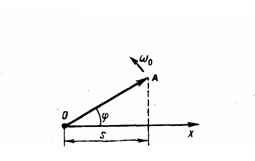
В
физике часто используется другой метод,
отличающийся от метода вращающегося
вектора амплитуды лишь по форме. В
данном методе колеблющуюся величину
представляют комплексным числом.
Используя
формулу Эйлера, для комплексных чисел

Значит
уравнение
гармонического колебания можно
представить в комплексной форме:  (2)
(2)
Вещественная
часть формулы (2) : 
есть
гармоническое колебание. Обозначение
Re вещественной части условимся опускать
и (2) записывать в форме

В
теории колебаний уславливаются, что
колеблющаяся величина s равна вещественной
части комплексного выражения, стоящего
в этом равенстве справа.
17 Сложение одинаково направленных гармонических колебаний.
Колеблющееся
тело может принимать участие в нескольких
колебательных процессах, тогда колебания
необходимо сложить.
Сложим
гармонические колебания одного
направления и одной частоты:

Воспользовавшись
методом вращающегося вектора амплитуды
. Построим векторные диаграммы
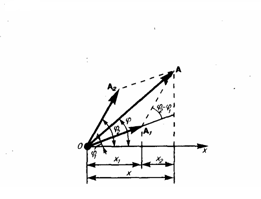
Так
как векторы А1 и А2 вращаются с одной
угловой скоростью ω0,
то разность фаз (φ2
–φ1)
между ними остается постоянной.
Уравнение результирующего колебания
будет 
Амплитуда
А и начальная фаза φ соответственно
определяются выражениями

(1)

Значит,
тело, участвуя в двух гармонических
колебаниях одного направления и
одинаковой частоты, совершает при этом
также гармоническое колебание в том
же направлении и с той же частотой, что
и складываемые колебания. Амплитуда
результирующего колебания зависит от
разности фаз (φ2 - φ1)
складываемых колебаний.
Исследуем
выражение (1) в зависимости от разности
фаз (φ2
- φ1):
1)
φ2
- φ1
= ±2mπ (m = 0, 1, 2, ...), тогда A=A1+A2,
т. е. амплитуда результирующего колебания
А будет равна сумме амплитуд складываемых
колебаний;
2)
φ2
- φ1
= ±(2m+1)π (m = 0, 1, 2, ...), тогда A=|A1–A2|,
т. е. амплитуда результирующего колебания
будет равна разности амплитуд складываемых
колебаний.
Биения
Периодические
изменения амплитуды колебания, которые
возникают при сложении двух гармонических
колебаний одинакового направления с
близкими частотами, называются биениями.
Пусть
амплитуды складываемых колебаний равны
А, а частоты равны ω и ω+Δω, причем Δω<<ω.
Выберем начало отсчета так, чтобы
начальные фазы обоих колебаний были
равны нулю:

Складывая
эти выражения и учитывая, что во втором
сомножителе Δω/2<<ω, получим

Результирующее
колебание можно считать как гармоническое
с частотой ω , амплитуда Аσ которого
изменяется по следующему периодическому
закону:

Частота
изменения Аσ в два раза больше частоты
изменения косинуса (так как берется по
модулю), т. е. частота
биений равна разности частот складываемых
колебаний:
 Период
биений
Период
биений
19. Сложение взаимно-перпендикулярных гармонических колебаний. Фигуры Лиссажу.
Найдем
результат сложения двух гармонических
колебаний одинаковой частоты ω, которые
происходят во взаимно перпендикулярных
направлениях вдоль осей х и у. Начало
отсчета для простоты выберем так, чтобы
начальная фаза первого колебания была
равна нулю, и запишем это в виде

где
α — разность фаз обоих колебаний, А и
В равны амплитудам складываемых
колебаний. Уравнение траектории
результирующего колебания определим
исключением из формул. Записывая
складываемые колебания как

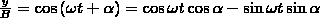
и
заменяя во втором уравнении  на
на  и
и  на
на
 , найдем после преобразований уравнение
эллипса, у которого оси ориентированы
произвольно относительно координатных
осей:
, найдем после преобразований уравнение
эллипса, у которого оси ориентированы
произвольно относительно координатных
осей:

Поскольку
траектория результирующего колебания
имеет форму эллипса, то такие колебания
называются эллиптически
поляризованными.
 Размеры
осей эллипса и его ориентация зависят
от амплитуд складываемых колебаний и
разности фаз α. Рассмотрим некоторые
частные случаи, которые представляют
для нас физический интерес:
Размеры
осей эллипса и его ориентация зависят
от амплитуд складываемых колебаний и
разности фаз α. Рассмотрим некоторые
частные случаи, которые представляют
для нас физический интерес:
Разность
фаз α=0


α=π/2


α=π/4

Если
частоты омега складываемых взаимно
перпендикулярных колебаний имеют
различные значения, то замкнутая
траектория результирующего колебания
довольно сложна. Замкнутые
траектории, прочерчиваемые точкой,
которая совершает одновременно два
взаимно перпендикулярных колебания,
называются фигурами Лиссажу.
Вид этих замкнутых кривых зависит от
соотношения амплитуд, разности фаз и
частот складываемых колебаний. На рис.
даны фигуры Лиссажу для различных
соотношений частот (даны слева) и
разностей фаз (даны вверху; разность
фаз равна φ).
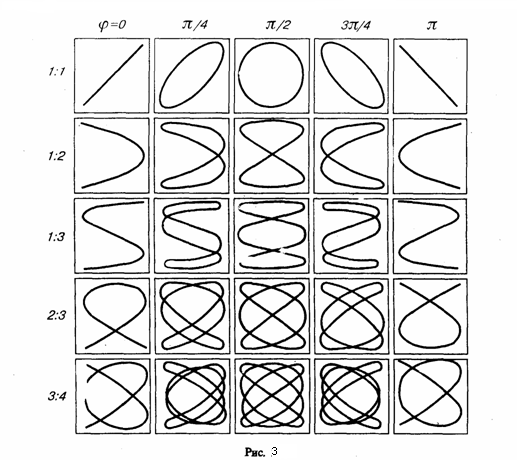
20.
Гармонический осциллятор. Дифференциальное
уравнение гармонического осциллятора.
Примеры гармонических осцилляторов.Гармоническим
осциллятором называется система,
которая совершает колебания, описываемые
выражением вида d2s/dt2
+ ω02s
= 0 или

две
точки сверху - двукратное дифференцирование
по времени. Колебания гармонического
осциллятора есть важный пример
периодического движения и служат точной
или приближенной моделью во многих
задачах классической и квантовой
физики. В качестве примеров гармонического
осциллятора могут быть пружинный,
физический и математический маятники,
колебательный контур (для токов и
напряжений настолько малых, что можно
было бы элементы контура считать
линейными).
Математический маятник, физический маятник, груз на пружине, колебательный контур без потерь энергии.
Математический
маятник
— это идеализированная система,
состоящая из материальной точки массой
m, которая подвешена на нерастяжимой
невесомой нити, и которая колеблется
под действием силы тяжести. Хорошее
приближение математического маятника
есть небольшой тяжелый шарик, который
подвешен на длинной тонкой нити. Момент
инерции математического маятника
J=ml2
(l-длина
маятника)
Период
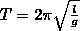
Физический
маятник
— это твердое тело, которое совершает
колебания под действием силы тяжести
вокруг неподвижной горизонтальной
оси, которая проходит через точку О,
не совпадающую с центром масс С тела
Момент
M возвращающей силы
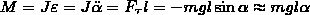
где
J — момент инерции маятника относительно
оси, которая проходит через точку
подвеса О, l – расстояние между осью и
центром масс маятника, Fτ ≈ –mgsinα ≈
–mgα — возвращающая сила
Циклическая
частота
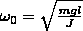
Период
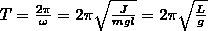
Пружинный
маятник
— это груз массой m,
который подвешен на абсолютно упругой
пружине и совершает гармонические
колебания под действием упругой силы
F
= –kx,
где k
— жесткость пружины. Уравнение движения
маятника имеет вид
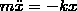 или
или
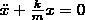
Циклическая
частота
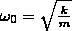
Период
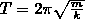
Колебательный
контур
— цепь, которая состоит из последовательно
включенных резистора сопротивлением
R, катушки индуктивностью L, и конденсатора
емкостью С.
По
закону Ома, для контура, который содержит
резистор сопротивлением R, катушку
индуктивностью L, и конденсатор емкостью
С
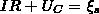
где
IR—напряжение на резисторе, UC
=  - напряжение на конденсаторе, ξs
= -L
- напряжение на конденсаторе, ξs
= -L – ЭДС самоиндукции, которая возникает
в катушке при протекании в ней переменного
тока (ξs
– единственная ЭДС в контуре).
– ЭДС самоиндукции, которая возникает
в катушке при протекании в ней переменного
тока (ξs
– единственная ЭДС в контуре).
Полная
энергия
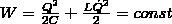
Период
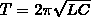
Собственная
частота контура
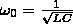
22.Энергия механических и электрических гармонических колебаний.
Кинетическая
энергия материальной точки, которая
совершает прямолинейные гармонические
колебания:
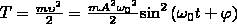
Потенциальная
энергия материальной точки, которая
совершает гармонические колебания,
будет равна:
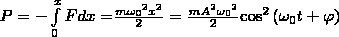 =1/2
*kA2
=1/2
*kA2
Для
механических колебаний справедлив
закон сохранения энергии.
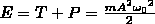 =const
=const
В
любой момент времени сумма потенциальной
и кинетической энергии колеблющегося
тела остается постоянной и равной этой
сумме в любой другой момент времени. В
процессе колебаний происходит превращение
потенциальной энергии в кинетическую
и обратно. В крайних точках отклонения
(амплитудное значение) вся энергия
маятника - потенциальная энергия. При
прохождении положения равновесия - вся
энергия кинетическая, скорость маятника
максимальна.
В
случае электрических колебаний энергия
в конуре : D
представляет собой сумму энергии
электрического поля, запасенной между
обкладками конденсатора, и энергии
магнитного поля, запасенной в катушке
с индуктивностью.
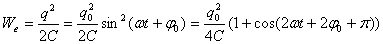 (энергия
электрического поля конденсатора)
(энергия
электрического поля конденсатора)
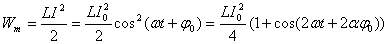 (энергия
магнитного поля катушки)
(энергия
магнитного поля катушки)
Полная
энергия в контуре остается неизменной:
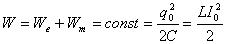
23.Затухающие
механические колебания. Коэффициент
затухания, логарифмический декремент
затухания. Добротность.Затухающие
колебания
– колебания, у которых амплитуды из-за
потерь энергии колебательной системой
с течением времени убывают. Простейшим
механизмом убывания энергии колебаний
есть ее превращение в теплоту вследствие
трения в механических колебательных
системахδ
=  — коэффициент
затухания. (количественная
характеристика сопротивления колеблющейся
системы колебательному движению)
— коэффициент
затухания. (количественная
характеристика сопротивления колеблющейся
системы колебательному движению)
Дифференциальное
уравнение свободных затухающих колебаний
маятника (механических колебаний)

Колебания
маятника подчиняются закону:

Где
частота 
Если
A(t)
и А(t
+ Т) — амплитуды двух последовательных
колебаний, соответствующих моментам
времени, которые отличаются на период,
то отношение

называется
декрементом
затухания,
а его логарифм

— логарифмическим
декрементом затухания;
Ne
— число колебаний, которые совершаются
за время уменьшения амплитуды в е раз.
Логарифмический декремент затухания
является постоянной величиной для
данной колебательной системы.
Для
характеристики колебательной системы
также применяют понятие добротности
Q,
которая равна

24.
Затухающие электрические колебания.
Коэффициент затухания, логарифмический
декремент затухания. Добротность.Затухающие
колебания
– колебания, у которых амплитуды из-за
потерь энергии колебательной системой
с течением времени убывают.
Простейшим
механизмом убывания энергии колебаний
есть излучения электромагнитной энергии
в электрических колебательных
системах. коэффициент
затухания. (количественная
характеристика сопротивления колеблющейся
системы колебательному движению)
коэффициент
затухания. (количественная
характеристика сопротивления колеблющейся
системы колебательному движению)
Дифференциальное
уравнение свободных затухающих колебаний
заряда в контуре (при R≠0)
Колебания
заряда подчиняются закону

С
частотой равной Если
A(t)
и А(t
+ Т) — амплитуды двух последовательных
колебаний, соответствующих моментам
времени, которые отличаются на период,
то отношение
Если
A(t)
и А(t
+ Т) — амплитуды двух последовательных
колебаний, соответствующих моментам
времени, которые отличаются на период,
то отношение
называется
декрементом
затухания,
а его логарифм
—
логарифмическим
декрементом затухания;
Ne
— число колебаний, которые совершаются
за время уменьшения амплитуды в е раз.
Логарифмический декремент затухания
является постоянной величиной для
данной колебательной системы.
Для
характеристики колебательной системы
также применяют понятие добротности
Q,
которая равна

Вынужденные колебания. Зависимость амплитуды и фазы вынужденных колебаний от частоты внешнего гармонического воздействия. Явление резонанса.
Колебания,
которые возникают под действием внешней
периодически изменяющейся силы или
внешней периодически изменяющейся
ЭДС, называются соответственно
вынужденными
механическими и вынужденными
электромагнитными колебаниями.
амплитуда
А смещения (заряда) имеет максимум.
Чтобы определить резонансную частоту
ωrez
, — частоту, при которой амплитуда А
смещения (заряда) будет максимальна, —
нужно найти максимум функции
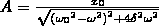
Продифференцировав
выражение под корнем по ω и приравняв
его нулю, получим условие, из которого
найдем ωrez
:
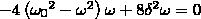
Это
равенство верно при
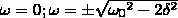 ,
у которых только выражение со знаком
плюс имеет физический смысл. Значит,
резонансная
частота
,
у которых только выражение со знаком
плюс имеет физический смысл. Значит,
резонансная
частота
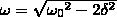
Явление
резкого возрастания амплитуды вынужденных
колебаний при приближении частоты
вынуждающей силы (частоты вынуждающего
переменного напряжения) к частоте,
равной или близкой собственной частоте
колебательной системы, называется
резонансом
(соответственно механическим или
электрическим). При ω02
>> δ2
значение ωrez
практически
равно собственной частотой ω0
колебательной системы.
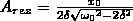
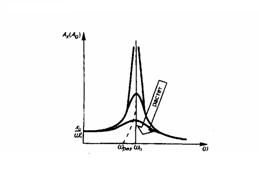
зависимости
амплитуды вынужденных колебаний от
частоты при различных значениях δ
чем
меньше δ, тем выше и правее лежит максимум
данной кривой. Если ω→0, то все кривые
достигают одного в того же, не равного
нулю, предельного значения x0/ω02
, которое называется статическим
отклонением. В случае механических
колебаний x0/ω02
= F0/(mω02)
, в случае электромагнитных – Um/(Lω02)
при
малом затухании (ω02
>> δ2)
резонансная амплитуда смещения (заряда)
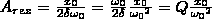
Зависимость
φ от ω при разных значениях δ графически
изображена на рис. 3, из которого вытекает,
что при изменении ω изменяется и сдвиг
фаз φ.
при
ω=0 φ=0, а при ω=ω0
независимо от значения коэффициента
затухания φ = π/2, т. е. сила (напряжение)
опережает по фазе колебания на
π/2. При дальнейшем росте ω сдвиг фаз
возрастает и при ω>>ω0
, т. е. φ→π фаза колебаний почти
противоположна фазе внешней силы
(переменного напряжения). Множество
кривых, изображенных на рис. 3, называется
фазовыми резонансными кривыми.
прикладная
акустика, радиотехника, электротехника
используют явление резонанса.
26Колебательный контур. Вынужденные колебания тока в цепи. Резонанс напряжений.
Колебательный
контур — осциллятор, представляющий
собой электрическую цепь, содержащую
соединённые катушку индуктивности и
конденсатор. В такой цепи могут
возбуждаться колебания тока (и
напряжения).
Колебательный
контур — простейшая система, в которой
могут происходить свободные
электромагнитные колебания
Резонансная
частота контура определяется так
называемой формулой Томсона:
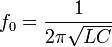
Процессы,
возникающие в электрических цепях под
действием внешнего периодического
источника тока, называются вынужденными
колебаниями.
Вынужденные
колебания, в отличие от собственных
колебаний в электрических цепях,
являются незатухающими. Внешний источник
периодического воздействия обеспечивает
приток энергии к системе и не дает
колебаниям затухать, несмотря на наличие
неизбежных потерь.
Если
в цепи переменного тока, который содержит
последовательно включенные резистор,
катушку индуктивности и конденсатор
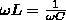 (1)
(1)
то
угол сдвига фаз между током и напряжением
становится равным нулю (φ=0), т. е. изменения
тока и напряжения происходят синфазно.
Выражению (1) удовлетворяет частота
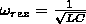
В
этом случае полное сопротивление цепи
Z (см. предыдущий раздел) становится
наименьшим, равным при этом активному
сопротивлению R цепи, и ток в цепи
задается этим сопротивлением, принимая
максимальные (возможные при данном Um)
значения. При этом падение напряжения
на активном сопротивлении равно внешнему
напряжению, которое приложено к цепи
(UR=U), а падения напряжений на катушке
индуктивности (UL) и конденсаторе (UC)
одинаковы по амплитуде и противоположны
по фазе. Это явление имеет название
резонанс
напряжений
(последовательный резонанс)
В
случае резонанса напряжений
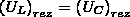
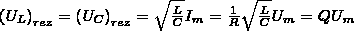
где
Q — добротность контура
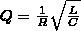

![]()

![]() Соленоид
можно представить в виде системы
одинаковых круговых
токов с общей прямой
осью.
Соленоид
можно представить в виде системы
одинаковых круговых
токов с общей прямой
осью.
![]()
![]() перпендикулярен
плоскости витка, т.е. линии
магнитной индукции имеют
направление параллельное оси
соленоида внутри
и вне его.
перпендикулярен
плоскости витка, т.е. линии
магнитной индукции имеют
направление параллельное оси
соленоида внутри
и вне его.![]()
![]()
![]() и
и
![]() т.е
т.е
![]()
![]()
![]()
![]()
![]() (в
системе СИ)
(в
системе СИ)
![]() — электродвижущая
сила, действующая вдоль произвольно
выбранного контура,
— электродвижущая
сила, действующая вдоль произвольно
выбранного контура,![]() — магнитный
поток через поверхность, натянутую
на этот контур.
— магнитный
поток через поверхность, натянутую
на этот контур.![]() ]
Знак
«минус» в формуле отражает правило
Ленца,
]
Знак
«минус» в формуле отражает правило
Ленца,
![]()
![]() —
число
витков,
—
число
витков,![]() :
:![]() .
.![]() называется коэффициентом
самоиндукции или индуктивностью контура
(катушки).
называется коэффициентом
самоиндукции или индуктивностью контура
(катушки).![]() —
магнитный поток,
—
ток в контуре,
—
индуктивность.
—
магнитный поток,
—
ток в контуре,
—
индуктивность.![]() .
.![]() .
.![]() внутри
катушки является фактически постоянной
и (приближенно) равна
внутри
катушки является фактически постоянной
и (приближенно) равна![]()
![]() − магнитная
постоянная,
−
число витков,
− магнитная
постоянная,
−
число витков, ![]() −
ток и
−
ток и ![]() −
длина катушки. Пренебрегая краевыми
эффектами на концах соленоида,
получим[10],
что потокосцепление через катушку
равно плотности потока
,
умноженному на площадь поперечного
сечения
−
длина катушки. Пренебрегая краевыми
эффектами на концах соленоида,
получим[10],
что потокосцепление через катушку
равно плотности потока
,
умноженному на площадь поперечного
сечения ![]() и
число витков
:
и
число витков
:![]()
![]()
![]() — относительную
магнитную проницаемость[11] сердечника:
— относительную
магнитную проницаемость[11] сердечника:![]()
![]()
![]()
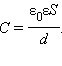 Поэтому
Поэтому ![]()
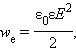
 Индукционное
электрическое поле является
вихревым.
Направление силовых
линий вихревого эл. поля совпадает с
направлением индукционного
тока
Индукционное электрическое
поле имеет совершенно другие свойства
в отличии от электростатического поля.
Индукционное
электрическое поле является
вихревым.
Направление силовых
линий вихревого эл. поля совпадает с
направлением индукционного
тока
Индукционное электрическое
поле имеет совершенно другие свойства
в отличии от электростатического поля.![]() через
некоторую поверхность[4]
через
некоторую поверхность[4] ![]() :
:![]()

![]() )
)![]()
![]() )
[ν]=Гц
)
[ν]=Гц![]()
![]()
![]()

![]()
![]() (2)
(2)![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() Период
биений
Период
биений![]()
![]()
![]()
![]()
![]() на
на ![]() и
и ![]() на
на
![]() , найдем после преобразований уравнение
эллипса, у которого оси ориентированы
произвольно относительно координатных
осей:
, найдем после преобразований уравнение
эллипса, у которого оси ориентированы
произвольно относительно координатных
осей:![]()
 Размеры
осей эллипса и его ориентация зависят
от амплитуд складываемых колебаний и
разности фаз α. Рассмотрим некоторые
частные случаи, которые представляют
для нас физический интерес:
Размеры
осей эллипса и его ориентация зависят
от амплитуд складываемых колебаний и
разности фаз α. Рассмотрим некоторые
частные случаи, которые представляют
для нас физический интерес:![]()

![]()

![]()

![]()
![]()
![]()
![]()
![]()
![]() или
или
![]()
![]()
![]()
![]()
![]() - напряжение на конденсаторе, ξs
= -L
- напряжение на конденсаторе, ξs
= -L![]() – ЭДС самоиндукции, которая возникает
в катушке при протекании в ней переменного
тока (ξs
– единственная ЭДС в контуре).
– ЭДС самоиндукции, которая возникает
в катушке при протекании в ней переменного
тока (ξs
– единственная ЭДС в контуре).
![]()
![]()
![]()
![]()
![]() =1/2
*kA2
=1/2
*kA2![]() =const
=const![]() (энергия
электрического поля конденсатора)
(энергия
электрического поля конденсатора)![]() (энергия
магнитного поля катушки)
(энергия
магнитного поля катушки)![]()
![]() — коэффициент
затухания. (количественная
характеристика сопротивления колеблющейся
системы колебательному движению)
— коэффициент
затухания. (количественная
характеристика сопротивления колеблющейся
системы колебательному движению)![]()
![]()
![]()
![]()
![]()
![]()
![]() коэффициент
затухания. (количественная
характеристика сопротивления колеблющейся
системы колебательному движению)
коэффициент
затухания. (количественная
характеристика сопротивления колеблющейся
системы колебательному движению)![]()
![]()
![]() Если
A(t)
и А(t
+ Т) — амплитуды двух последовательных
колебаний, соответствующих моментам
времени, которые отличаются на период,
то отношение
Если
A(t)
и А(t
+ Т) — амплитуды двух последовательных
колебаний, соответствующих моментам
времени, которые отличаются на период,
то отношение![]()
![]()
![]()
![]() ,
у которых только выражение со знаком
плюс имеет физический смысл. Значит,
резонансная
частота
,
у которых только выражение со знаком
плюс имеет физический смысл. Значит,
резонансная
частота
![]()
![]()

![]()

![]()
![]() (1)
(1)![]()
![]()
![]()
![]()
