4.1 Металічні кластери і кулонівський вибух

Оболонкова електронна структура виявлена у кластерів благородних металів. Прикладом можуть бути кластери з атомів срібла. Встановлено, що найбільша енергія зв’язку між атомами срібла існує в кластера Ag₁₇, для якого заповнена оболонка містить 18 електронів. Квантово-механічні розрахунки показали, що є правомірним використовувати оболонкову модель майже для всіх кластерів за винятком Ag₇ і Ag₉.

Характерною особливістю кластерів перехідних металів є те, що їх атоми можуть знаходитися в різних окисних станах. З цієї причини їх властивості не можуть описуватися простою оболонковою моделлю, як це має місце для кластерів простих металів. Кластери з атомів перехідних елементів часто відносять до групи магнітних кластерів. Такі кластери володіють магнітним моментом

4,2 Квантово-розмірними називають такі системи, в яких проявляються квантові властивості, що залежать від розмірів цієї системи і її форми. У об’ємних матеріалах розглядають трьохвимірні електронні системи макроскопічних розмірів. У такому випадку електрони провідності делокалізовані і переміщуються вільно в межах всього середовища. Коли ми будемо зменшувати один або більше розмірів матеріалу до величин, близьких до кількох міжатомних відстаней, ситуація з точки зору квантово-механічних властивостей суттєво змінюватиметься. В першу чергу делокалізація ставатиме неможливою і електрони залишатимуться локалізованими. При цьому, як вже відзначалось, таке зменшення розмірів матеріалу може відбуватися в межах різної форми. Якщо ми будемо зменшувати лише один розмір тіла, а решту два залишаємо без змін, то ми отримаємо тонкий лист, товщина якого дорівнюватиме декілька нанометрів. Електрони провідності у такому випадку будуть делокалізовані у площині листа і будуть локалізовані по найменшому розміру. Сформований таким способом об’єкт називають квантовою ямою, або двохвимірною квантовою системою (2Д-системою). У випадку зменшення двох розмірів до значень кількох нанометрів отримаємо інший тип структури – квантовий дріт або одновимірну квантову систему (1Д-систему). Електрони делокалізовані і вільно рухаються вздовж дроту, але є локалізовані у поперечних напрямках. І накінець, коли зменшуватимемо розміри масивного тіла у всіх трьох розмірах до нанометрового масштабу, то отримаємо квантову точку, або як її ще називають квантову систему (0Д-систему). Ця квантова точка може мати вигляд нанорозмірного куба, кулі, циліндра чи іншого геометрично просторового тіла і електрони будуть локалізованими у всіх трьох напрямках, а делокалізації взагалі не буде. Зрозуміло, що необхідно розглянути поведінку електронної підсистеми в такого типу структурах і вплив особливостей цієї поведінки на енергетичні характеристики.

Важливою характеристикою електронної підсистеми є густина станів, якою називають кількість станів у одиничному інтервалі енергій.

Якщо говорити точніше, то у випадку двовимірних структур функція має форму сходинок, тобто є сталою з певним значенням на різних енергетичних інтервалах (Рис. 10.1). Таким чином ми прийшли до важливого висновку про залежність функції густини станів від розмірності об’єкта.

6,1 Магнітні кластери і вуглецеві кластери. Кластерна структура води.

Вуглецеві кластери займають особливе місце серед інших типів кластерів. Це стосується також і вуглецю, який є проміжним між іншими елементами. Вуглецеві кластери поділяють на малі і великі. Коли кількість атомів у кластері менша 24, то їх називають малими, а коли більша, то великі. Великі вуглецеві кластери ще називають фулеренами і вуглецевими нанотрубками. Цілком можливо, що серед великих вуглецевих кластерів будуть знайдені також інші мікроскопічні об’єднання атомів.

Найпростішим і найпоширенішим видом малих вуглецевих кластерів є сажа. Масспектрометричним методом встановлено, що існують магічні числа для малих кластерів С_n (n=7, 11, 15, 19 і 23). Дослідження процесів фотофрагментації показало, що основним фрагментом є нейтральні кластери С₃, а в деяких випадках і С₅. Атоми вуглецю в кластерах формують щільні структурні форми з деякою -гібридизацію електронних станів. Квантовохімічні розрахунки показали, що в нейтральних кластерах вуглецю можуть існувати стабільні ланцюжки з кількістю атомів не більше 9. Коли атомів у ланцюжку стає більше, то ланцюжок перетворюється у кільце.

Енергії іонізації вуглецевих кластерів також проявляють відповідність з магічними числами для позитивно заряджених кластерів у формі кільця. Енергія іонізації нейтральних кластерів, для яких n=4k+3 (n=11, 15, 19, 23) є меншою, ніж енергія іонізації, що відповідає нейтральним кластерам з магічними числами n=10, 14 і т.д із заповненою електронною оболонкою.

Вода володіє відносно складною структурою і багато її особливостей досі не мають строгого пояснення. Цій рідині характерна чітко виражена здатність до самоорганізації завдяки утворенню водневих зв’язків.. Кластери води зазвичай розраховуються теоретично лише для кількох десятків молекул або поблизу міжфазної границі.

Необхідно відзначити, що кластери води утворюють не лише воду, а також і лід. Ці кластери приймають участь у формуванні хмар, дощу та в багатьох інших процесах як, наприклад, аномальному розсіянні світла на хмарах. Кластери води утворюються також в процесі гідратації газових або молекулярних кластерів, під час гідратації макромолекул та білків.

6,2 Магнітоопір є важливою фізичною характеристикою матеріалів, яка відображає особливості їх внутрішньої будови. Загалом магнітоопором називають ефект зміни електричної провідності матеріалу, коли його поміщають у магнітне поле. Кількісно магнітоопір оцінюють за допомогою співвідношення:

,

де – електроопір за умови відсутності поля;

– електроопір в полі .

Ефект магнітоопору ще називають гальваномагнітним ефектом і його фізичну природу спочатку вивчали на класичних феромагнетиках ( ). Виявилось, що величина магнітоопору за умови паралельної орієнтації поля і струмускладає при кімнатній температурі в залізі і нікелі відповідно 0,07% і 1,5%

У 1988р. у штучно створеній надгратці Fe/Cr вперше спостерігали гігантський магнітоопір. Величина за умов і перевищувала 90%. У цій надгратці феромагнітні шари товщиною приблизно 3нм чергувались з неферомагнітними шарами хрома товщиною 1-2нм (рис. 8.2).

Рис. 8.2. Атомні шари заліза і хрому у багатошаровій структурі.

Амплітуда гігантського магнітоопору залежить від індивідуальних характеристик матеріалів, з яких складаються парні шари, а також від товщини тих шарів.

Гігантський магнітоопір пояснюють з використанням зонної теорії. Причиною його є механізм неоднакового розсіяння двох груп електронів, які відрізняються орієнтацією спінів відносно напрямку намагніченості магнітної структури, яка розсіює електрони. Для реалізації такого механізму потрібно щоб середня довжина вільного пробігу суттєво відрізнялася для електронів з напрямками спінів “вгору” і “вниз

7,1 Для розрахуку термодинамічних властивостей кластерів використовують певну модель і розраховують потенціальну енергію. Найпростіше цю енергію можна оцінити за допомогою суми парних потенціалів Ленарда-Джонс ,

де – відстань між -м і -м атомами;

– значення енергії в мінімумі потенціала;

– міжатомна відстань, при якій мінімальне.

Недоліком цієї формули є те, що вона не вруховує взаємодії вищого порядку ніж парного. Тому, в загальному випадку потенціальну енергію кластера розраховують таким чином:

.

Найпоширенішими є три основних методи розрахунку термодинамічних функцій кластера: метод нормальних коливань мод, метод молекулярної динаміки і метод Монте-Карло. В першому з цих методів кластер розглядають як -атомну молекулу ідеального газу, енергія якої складається з енергії Е_тр трансляційного руху і внутрішньої енергії Е_вн руху атомів відносно центра мас. Своєю чергою Е_вн можна розкласти на незалежні обертальну Е_об і коливну Е_кол частини при умові, що нехтується вплив обертання кластера на його коливні енергетичні рівні. .

.

метод молекулярної динаміки грунтується на послідовному розрахунку положення і швидкості кожного атома з інтервалом часу під дією сил, які визначаються градієнтом потенціальної енергії. Термодинамічні функції розраховують зі значення повної енергії, яка є сумою потенціальної і кінетичної енергії кластера.

Останній з використовуваних тепер методів – метод Монте-Карло полягає в тому, що точний статистичний вираз для обчислення середнього значення будь-якої фізичної величини замінюється наближеним усередненим значенням цієї величини по великій кількості випадкових конфігурацій атомів. Ці конфігурації отримуються одна з одної під час послідовного випадкового переміщення тільки одного атома на обмежену відстань. Для кожної конфігурації оцінюють потенціальну енергію як суму парних взаємодій. Якщо при наступному кроці система переходить в стан з меншою енергією, то приймається нова конфігурація атомів. У протилежному випадку перехід у нову конфігурацію дозволяється лише за умови , де – випадкове число між 0 і 1, вибране за допомогою комп’ютера. Середня потенціальна енергія кластера цим методом визначається безпосередньо.

7,2 Як відомо, у напівпровідникових кластерах по аналогії до масивних напівпровідників існує енергетична щілина між валентною зоною і зоною провідності. У таких речовинах збудження кластера розглядають як збудження екситона, який є парою електрон-дірка, що зв’язані між собою слабким зв’язком. Електрон появляється у зоні провідності, і дірка у валентній зоні. Ділянка делокалізації екситона може суттєво перевищувати період кристалічної гратки масивного тіла, а у випадку нанокластера може бути співмірний або перевіищувати розмір кластера, що призводить до квантового обмеження.

Якщо відбувається рекомбінація випрмінювань генерованих електроном і діркою, то спостерігається у бік більших енергій зі зменшенням розміру кластера у спектрах люмінісценції..

Ширина ліній люмінісценції також залежить від розмірів кластера,

,

Це рівняння вказує, що зменшення розміру кластера спочатку призводить до зростання часу релаксації, оскільки перший вираз, який описує електрон-фононну взаємодію є домінуючий. При подальшому зменшенні розміра кластера вже спостерігається протилежна закономірність–час релаксації зменшується завдяки другому члену виразу. Крім голубого зсуву у нанокластерних матеріалах також спостерігається і червоний зсув. Він є властивий нанокластерам напівпровідників з великою забороненою зоною. Дія тиску на зонну структуру добре досліджена і вказує на перекривання хвильових функцій матеріала. У деяких напівпровідниках енергетична щілина зменшується зі збільшенням тиску і може навіть закритися. За таких критичних тисків матеріал переходить з напівпровідникового у металічних стан.

Крім енергетичних зсувів у спектрах поглинання і випромінювання, зміни ширини і часу вопромінювання для нанокластерів, збільшується інтенсивність випромінювання, яка виражається як збільшення сили осциляторів

8,1 метод Монте-Карло полягає в тому, що точний статистичний вираз для обчислення середнього значення будь-якої фізичної величини замінюється наближеним усередненим значенням цієї величини по великій кількості випадкових конфігурацій атомів. Ці конфігурації отримуються одна з одної під час послідовного випадкового переміщення тільки одного атома на обмежену відстань. Для кожної конфігурації оцінюють потенціальну енергію як суму парних взаємодій. Якщо при наступному кроці приріст потенціальної енергії системи виявиться меншим нуля, тобто система переходить в стан з меншою енергією, то приймається нова конфігурація атомів. У протилежному випадку перехід у нову конфігурацію дозволяється лише за умови , де – випадкове число між 0 і 1, вибране за допомогою комп’ютера. Вважається, що будь-яка конфігурація атомів є досяжною при достатньо великій кількості кроків. Середня потенціальна енергія кластера цим методом визначається безпосередньо.

Методи молекулярної динаміки і Монте-Карло приймають до уваги теплове розширення і ангармонізм коливань атомів при високих температурах, але не враховують квантових нульових коливань атомів, енергія яких складає суттєву частку від повної енергії кластера при низьких температурах. Також в цих методах результати розрахунку залежать від об’єму, який обмежує рух атомів кластера. Існує також ряд інших недоліків цих методів, які намагаються врахувати інші наближення.

Важливою характеристикою, яка використовується в термодинамічному описі поверхні є поверхневий натяг. Поява поверхні при утворенні кластера, наприклад в рідинному середовищі, призводить до збільшення енергії системи. У випадку кластерів їхня поверхня характеризується дуже малим радіусом кривизни, що відображається на зростанні тиску парів над викривленою поверхнею у порівнянні з плоскою.

Нуклеація і ріст нанокластерів з окремих атомів може відбуватися різними шляхами, але у більшості випадків вона здійснюється в порожнинах і на поверхні адсорбентів та поруватих систем, якими можуть бути оксиди кремнія та алюмінія, цеоліти, порувате вугілля тощо. Поруваті матриці дають змогу отримувати наносистеми шляхом просочування розчинами і проведення хімічної реакції в порожнині подібно як у мікро- чи нанореакторі. Утворення кластерів, які стають зародками нової фази в переохолодженій рідині і пересиченому розчині добре вивчено і викладено у багатьох підручниках з термодинаміки, матеріалознавства та інших дисциплін. Слід відзначити, що це стосується процесів, які відбуваються у нескінчено великих об’ємах. Коли об’єм малий, то спостерігаються певні особливості такої нуклеації і росту. Розглянемо це на прикладі порожнини, яка заповнена розчином зі змінною концентрацією атомів, з яких відбувається нуклеація.

8,2

Оптичні властивості так само як інші фізичні характеристики змінюються при переході від масивних твердих тіл до наносистем. Існує декілька чинників такої зміни, до яких в першу чергу можна віднести обмеження довжини вільного пробігу електрона. Змінюються різні оптичні характеристики (енергія переходів, час люмінісценції тощо).

Першою особливістю оптичних властивостей наносистем з металічних кластерів є те, що їх спектри поглинання характеризуються інтенсивною широкою смугою, яка не виявляється у масивних матеріалах. Ця смуга пов’язана з колективним збудженням електронів провідності і призводить до виразної кольорової гамми від червоного кольору до синього для розбавлених колоїдів благородних, лужних і рідкісноземельних металів. Збудження електронів провідності ще називають плазмонами . Плазмонний ефект полягає в резонансному поглинанні нанокластером падаючого електромагнітного випромінювання. Внаслідок дії електромагнітного поля електрони провідності у кластері зміщуються відносно позитивно зарядженого остова. Таке зміщення спричиняє силу, яка заставляє електрони рухатись у протилежному напрямку і вона є пропорційною до величини зміщення подібно до того як це має місце для гармонічного осцилятора. За умови співпадання власної частоти коливань електронів і частоти зовнішнього поля повинен спостерігатися резонансний ефект, пов’язаний зі збудженням власних коливань електронів. Опис колективного руху електронів на мові кванотової механіки призводить до поняття елементарних збуджень – плазмонів, які володіють енергією , де – власна частота плазмонів.

Найпростіший опис оптичних властивостей зроблено в класичній теорії Мі. Властивості нанокластерів і матриці можна охарактеризувати комплексною діелектричною проникливістю, яка з’являється як результат поглинання електромагнітного випромінювання

(рис. 7.1)

Рис. 7.1. Розрахунок спектрів плазмонного поглинання

кластерів срібла розміром 2; 4 і 6 нм-а) і розміром 4нм, розміщених в матриці зі змінною діелектричною сталою-б).

Зменшення розмірів кластера призводить до зменшення інтенсивності резонансного поглинання і збільшення величини піка.

9,1

Невпорядковані системи є загальним випадком існування структурних формувань, а кристалічні речовини є їх частинним випадком. Формування наночастинок в більшості випадків відбувається шляхом об’єднання кількох атомів в кластери, які після цього обєднуються в структурні комплекси більших розмірів. Такий процес може відбуватися різними шляхами, що в кінцевому випадку відображається на характеристиках сформованих об’єктів. Залежно від ступеня впорядкованості ними можуть бути аморфні речовини, квазікристали, фрактали, чи монокристали і кожний з них володіє певними специфічними властивостями. Зважаючи на це, доцільно розглядати невпорядковані системи як узагальнений рузультат об’єднання окремих кластерів в складніші структурні одиниці.

Невпорядковані системи часто розглядують з використанням такого поняття як безлад, під яким розуміють відхилення розподілу основних структурних елементів (атомів, молекул) від ідеального просторового розміщення

Розглядають декілька основних типи безладу: комірковий, заміщення, магнітний, “льодовий” та топологічний. Перший з них грунтується на тому, що більшість кристалічних речовин характеризується щільною атомною упаковкою.При такому розташуванні кожний з атомів намагається дотикатись до найбільшої кількості сусідів. Кристалографія розглядає різні варіанти такої будови, приймаючи атоми як кульки певного діаметра. Для того щоб врахуввати незаповнений об’єм між кульками вводять поняття комірки Вігнера-Зейтца. Для її побудови необхідно провести вектори, які з’єднують центр певного вибраного атома з центрами сусідніх атомів, а через середини векторів і перпендикулярно до них провести площини. Ці площини обмежуватимуть певний об’єм, який і називають коміркою Вігнера-Зейтца (рис. 2.1). Шляхом паралельного переносу цієї комірки вже можна заповнити весь об’єм кристалу без будь-яких порожнин.

Рис. 2.1. Побудова комірки Вігнера-Зейтца (а)

і поліедра Вороного(б).

Рузультати досліджень структури багатьох речовин з невпорядкованим розподілом атомів дозволили прийти до висновку, що їм також характерна щільна будова не дивлячись на ту що дального порядку немає, а проявляється лише ближній. В такому разі побудова комірки Вігнера-Зейтца трансформується в поліедр Вороного. В системах з ближнім порядком такі поледри будуть різними, але і тут простір заповнюватиметься повністю.

9,2 Як і більшість фізичних властивостей кластерних систем їх магнітні характеристики також є суттєво відмінні ніж у масивних матеріалах. Формування магнітних властивостей наноструктур визначається розмірними ефектами, впливом поверхні окремих кластерів, міжкластерною взаємодією, взаємодією кластерів з матрицею і способом міжкластерної організації. В наносистемах виявляють багато закономірностей у поведінці магнітних властивостей, які характерні масивним матеріалам, але водночас в них існують і зовсім нові явища, як наприклад, суперпарамагнетизм, магнітне квантове тунелювання тощо.

Для нанокластерів і наноструктур магнітні фазові переходи мають особливе значення, оскільки туту починають прявлятися багато нових порівняно з масивними матеріалами явищ. Наприклад, магнітне впорядкування у наносистемі може зникати скачком і наносистема переходить у парамагнітний стан, для якого характерне збереження магнітного впорядкування нижче точки Кюрі.

Використання терміну “тунелювання” для квантового переходу магнітного момента з метастабільного стану у рівноважний є дещо нетиповим. Дійсно, терміном “тунельний перехід” прийнято називати перехід (просочування) реальної частинки у просторі під потенціальним бар’єром.

Тунельний ефек просто інтерпретується на основі співвідношення невизначеностей Гейзенберга.

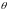Повертаючись до тунелювання намагніченості, можна бачити, що у цьому випадку також існує бар’єр, який розділяє метастабільний і стабільний стани, але по осі абсцис відкладається не реальна координата , а кутова зміна . Якщо необхідно визначити не переміщення частинки у просторі, а переорієнтацію магнітного момента чи спіна частинки через заборонений інтервал кутів, то які співвідношення ми можемо використати. Тут ми можемо провести деякі аналогії. Наприклад, порівняємо між собою формули для кінетичних енергій поступального руху і обертального .