Типы реакций связи

Нить, трос		Невесомый стержень	Гладкая поверхность		Шарнир на катках
Плоская система сил y x			Пространственная z система сил y x
Направляющая			Цилиндрический шарнир
Две направ-ляющие			Петля
Плоский шарнир			Сферический шарнир, подпятник
Жесткая заделка			Жесткая заделка

Примечание.

Для пространственной системы сил в случае цилиндрического шарнира или петли реакции связей изображены при наличии в реальной задаче второй опоры. При отсутствии второй опоры должны быть добавлены два реактивных момента относительно осей x и z.

В задачах на опрокидывание вместо уравнения моментов используется неравенство , где В – точка, относительно которой происходит опрокидывание.

Пример 1

2 Балка BD, закрепленная, как указано на рис. 34, находится в равновесии, и на нее действуют следующие силы: F₁=6Н, p=2Н/м, F=F=25Н (а=1м, h=2м, , DE==3м).

Определить реакции опор B и D в двух случаях: без учета и с учетом веса стержня DE.

Решения 2-х задач по алгоритму визуализированы.

Случай 1а (невесомый стержень DE).

Рис. 34

3 Один объект равновесия.

5 Равномерно распределенная на отрезке 3а нагрузка (рис. 34) заменена сосредоточенной силой P = p3a (рис. 35). Точка приложения силы находится в середине отрезка. Пара сил заменена моментом пары кН.

Опоры B и D (рис. 34) заменены реакциями опор: (рис. 35).

Силовая схема

Рис. 35

6 РПЛ

7

8 Из 1-го уравнения Н –10,39 Н,

из 2-го уравнения =18,00 Н, из 3-го уравнения 106,00 Нм.

9 Ответ: = –10,39 Н, =18,00 Н, =106,00 Нм.

Случай 1б (учитывается вес стержня DE – P₁=4Н)

3. Составная конструкция.

4. n=2

 = 1 (равновесие всей конструкции BDE)

3. Опоры в точках B и E заменены реакциями опор (рис. 36).

Силовая схема

Рис. 36

6 РПЛ

7

=2 (равновесие стержня DE)

5 Опоры D и E заменены реакциями опор: (рис. 37).

Силовая схема

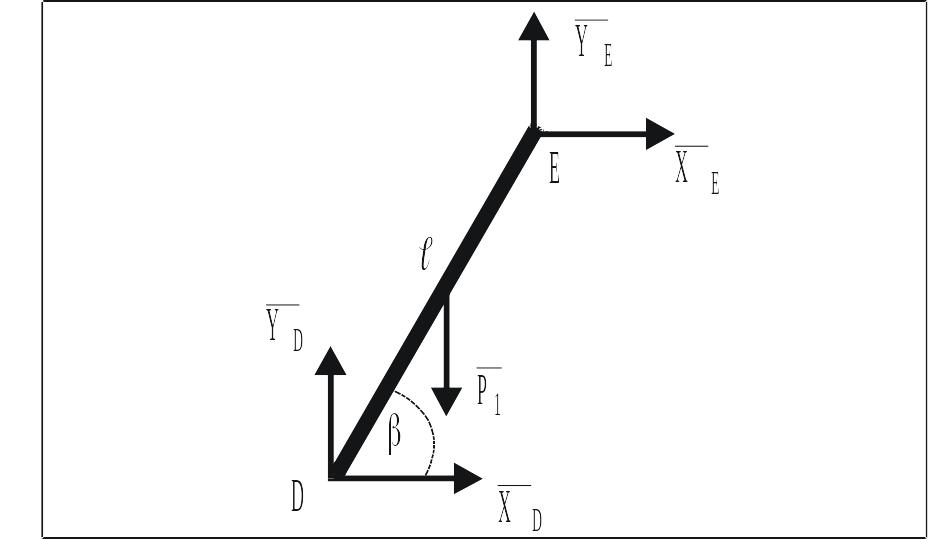
Рис. 37

6. РПЛ

7

8 Из 1-го уравнения ,

из 4-го уравнения ,

из 6-го уравнения ,

из 5-го уравнения ,

из 2-го уравнения ,

из 3-го уравнения .

9 Ответ: , , ,

, , .

Пример 2

2 Два стержня BD и DE соединенные шарнирно и закрепленные, как указано на рис. 38, находятся в равновесии и на них действуют следующие силы и моменты: Н, Н, Н/м, Н/м (а=2м, ).

Найти: реакции опор B, E и шарнира D.

Решение задачи по алгоритму визуализировано.

Рис. 38

3 Составная конструкция

4 n=2

Неизвестных реакций связи, действующих на систему двух стержней BD и DE – 4 (жесткая заделка B – 3, шарнир на катках E – 1, рис. 39). Уравнений равновесия для всей системы BDE – 3. Итак, три уравнения равновесия для четырех неизвестных. Для того чтобы найти дополнительные уравнения равновесия, рассматривается также равновесие стержня DE. Для этого составная конструкция разрезается по шарниру D. Именно поэтому задачи такого типа называются задачами на разрезные балки.

В точке D добавятся 2 неизвестные силы реакции связи, а уравнений равновесия дополнительно получится 3.

Итого: 6 (3+3) уравнений равновесия - 6 (4+2) неизвестных реакций связи.

=1 (равновесие всей конструкции BDE)

3. Силовая схема (здесь P=pa=2Н.)

Рис. 39

6 РПЛ

7

=2 (равновесие стержня DE)

5 Силовая схема

Рис. 40

6 РПЛ

7

8 Система шести уравнений 1-6 для шести неизвестных:

из 6-го уравнения Н 24,22 Н,

из 5-го уравнения Y_D = –9,00 Н, из 4-го уравнения Н 12,11 Н,

из 3-го уравнения 4 Н, из 2-го уравнения Н –13,92 Н,

из 1-го уравнения X_B = 16,11 Н.

9 Ответ: X_B =16,11 Н, Y_B = –13,92 Н, mom_B = – 75,94 Нм,

X_D =12,11 Н, Y_D = – 9,00 Н, N_E =24,22 Н.