Глава 5. Условия равновесия систем сил

1. Пространственная система сил

5.1.1. Геометрическая форма

Для равновесия произвольной пространственной системы сил, необходимо и достаточно, чтобы главный вектор и главный момент системы сил при приведении к любому центру были равны нулю:

(5.1)

Доказательство необходимости условий (5.1):

Пусть произвольная система сил находится в равновесии, т. е. ( ) ' 0. Приведя эту систему сил к центру О, получим:

.

Так как сила – главный вектор и пара сил, момент которой равен главному моменту друг друга уравновесить не могут, то необходимо, чтобы , что и требовалось доказать.

Доказательство достаточности условий (5.1):

Пусть . Предположим (метод от противного), что система сил ( ), не находится в равновесии, тогда, приведя эту систему сил к любому другому центру О₁, получим:

,

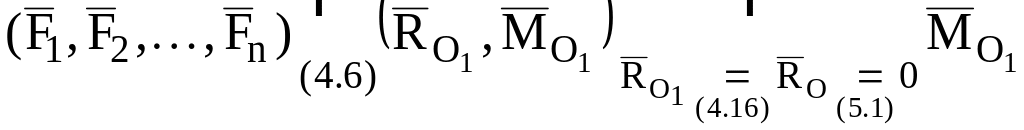т. е. система сил приводится к паре с моментом: .

Таким образом, для любого центра приведения главный вектор и главный момент равны нулю, следовательно ( ) ' 0 и наше предположение было неверно, т. е. система сил ( ), находится в равновесии.

5.1.2. Алгебраическая форма

Спроектировав соотношение (5.1) на оси декартовой системы координат с началом в центре приведения О и учтя связь моментов силы относительно точки и оси, получим следующие условия равновесия произвольной пространственной системы сил:

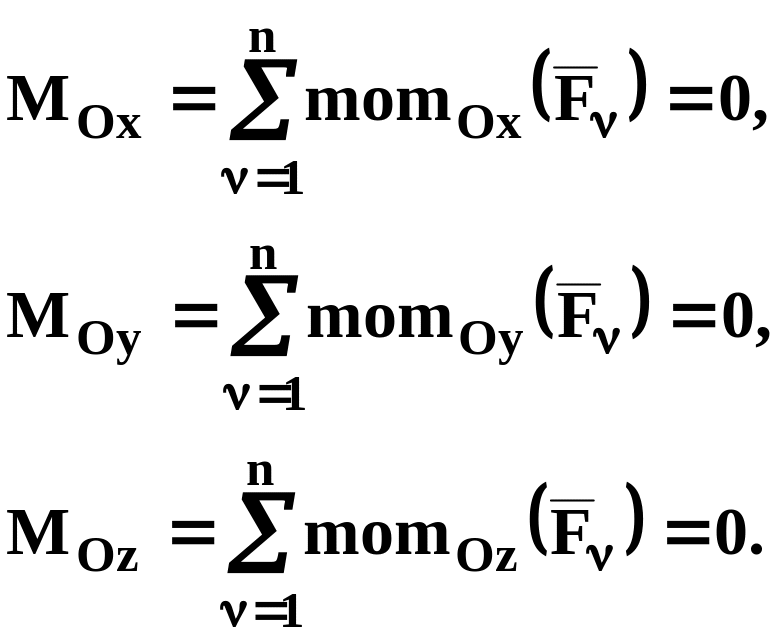(5.2)

Для равновесия произвольной пространственной системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на оси декартовой системы координат и суммы моментов всех сил относительно осей декартовой системы координат равнялись нулю.

Для равновесия пространственной системы параллельных сил, необходимо и достаточно, чтобы алгебраическая сумма величин этих сил была равна нулю и суммы моментов сил относительно двух координатных осей, лежащих в плоскости, перпендикулярной направлению линий действия сил, также были равны нулю:

(5.3)

5.2. Плоская система сил

5.2.1. Первая форма

В случае плоской системы сил, находящейся в плоскости хОу соотношения (5.2) и (5.3) примут вид:

(5.4)

Для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на оси x, y, лежащие в плоскости действия сил и алгебраическая сумма величин моментов всех сил относительно любой точки плоскости равнялись нулю.

Для равновесия плоской системы параллельных сил, необходимо и достаточно, чтобы алгебраические суммы величин этих сил и величин моментов сил относительно любой точки, находящейся в плоскости действия сил равнялись нулю:

(5.5)

Необходимые и достаточные условия равновесия плоской системы сил можно выразить еще в двух других формах.

5.2.2. Вторая форма

Для равновесия плоской системы сил, необходимо и достаточно чтобы алгебраические суммы величин моментов этих сил относительно трех точек, лежащих в плоскости действия сил и не расположенных на одной прямой, равнялись нулю:

(5.6)

Эта форма равновесия плоской системы сил также называется теоремой о трех моментах.

Доказательство необходимости условий (5.6):

Пусть плоская система сил, находится в равновесии: ( )'0. Из необходимости третьего уравнения (5.4) следует необходимость условий (5.6).

Доказательство достаточности условий (5.6):

Пусть выполняются условия (5.6). Предположим (метод от противного), что плоская система сил ( ), не находится в равновесии. Приведем эту систему сил к центру В, тогда

.

Если = 0, то система сил находится в равновесии. Предположим, что 0, т. е. что система сил не находится в равновесии. Применив дважды теорему Вариньона для точек D и E, получим:

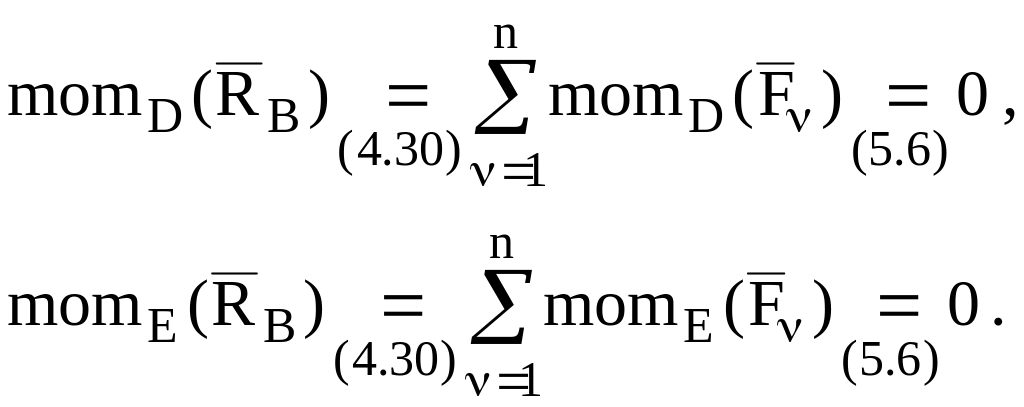
Из этих соотношений следует, что линия действия равнодействующей , приложенной в точке B проходит также через точки D и E, чего быть не может, так как точки B, D и E не расположены на одной прямой. Следовательно, наше предположение неверно и плоская система сил ( ) находится в равновесии.