8.2. Перший закон термодинаміки.

Якщо робочому тілу (газу) надати кількість тепла , відбувається зміна його внутрішньої енергії на величину , і газ виконує елементарну роботу , причому виконується рівність, яка є наслідком закону збереження енергії:

. (18)

Елементарна робота визначена формулою (13), а зміна внутрішньої енергії для ідеального газу є повним диференціалом:

. (19)

( – зміна температури). Звернемо увагу: зміна внутрішньої енергії визначається виключно параметрами початкового та кінцевого стану газів; значення роботи, яка виконана газом при переході із стану 1 до стану 2, залежить від ходу кривої p(T), тобто від характеру термодинамічного процесу.

В інтегральному вигляді перший закон термодинаміки можна представити для відомих ізопроцесів: кількість тепла, передана газу при переході із стану 1 до стану 2, визначається таким чином:

Ізобарний процес ( =const)	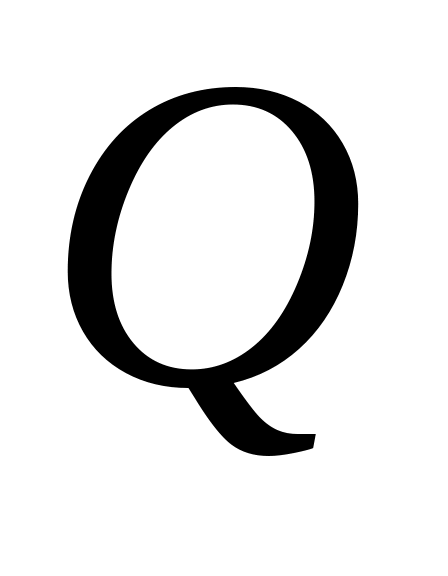= 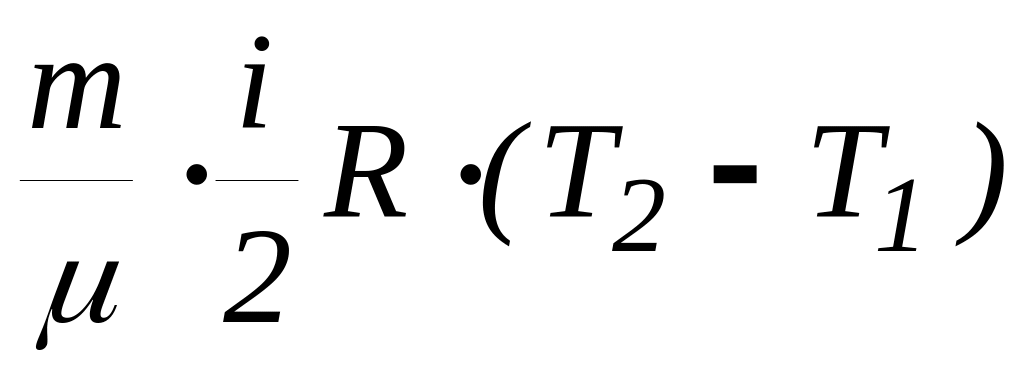+ ∙( 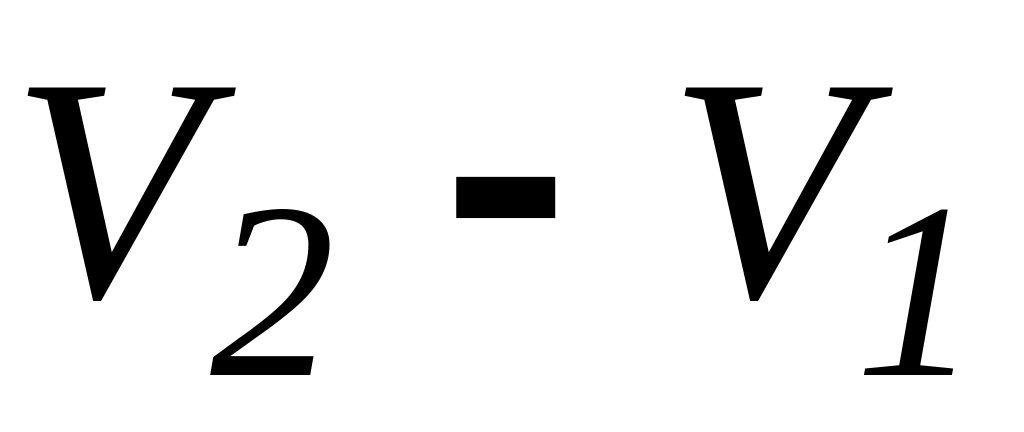)	(20)
Ізотермічний процес ( =const)		(21)
Ізохорний процес ( =const)	=	(22)

Теплоємністю тіла у даному термодинамічному процесі називають кількість тепла, яку необхідно надати тілу для збільшення його температури на 1 К

= . (23)

Для газів вводять молярні теплоємності (для одного молю, тобто ν =1 моль)

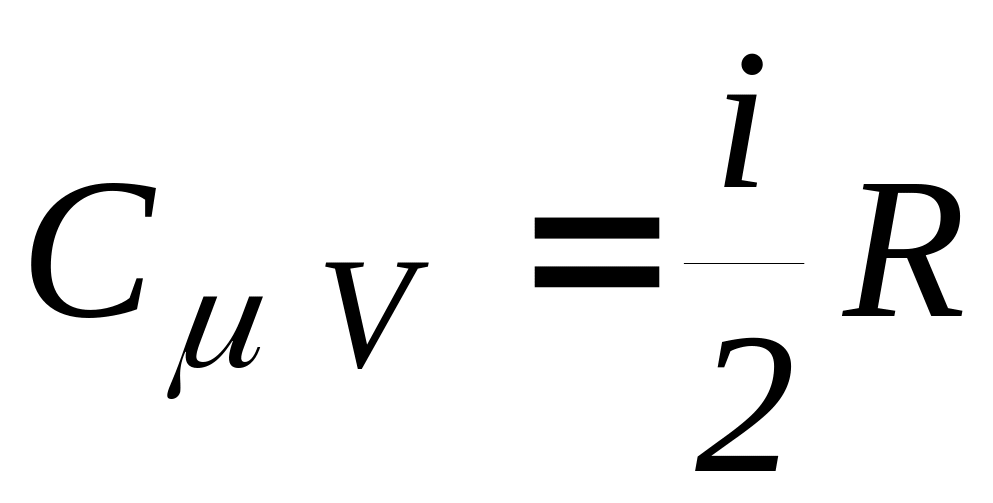
При =const		(24)
При =const	=	(25)
При =const		(26)

Внутрішня енергія довільної кількості газу (енергія теплового руху молекул) таким чином може бути записана з використанням молярної теплоємності при сталому об’ємі:

= . (27)

Підкреслимо, що молярна теплоємність визначається виключно числом ступенів свободи молекули газу.

Питома теплоємність газу (для одного кг, тобто m = 1 кг) зв’язана з молярною теплоємністю співвідношенням

= . (28)

8.3. Адіабатний процес.

Процес, який протікає без теплообміну з навколишнім середовищем, називають адіабатним процесом. Рівняння адіабатного процесу (рівняння Пуассону) можна записати у трьох варіантах

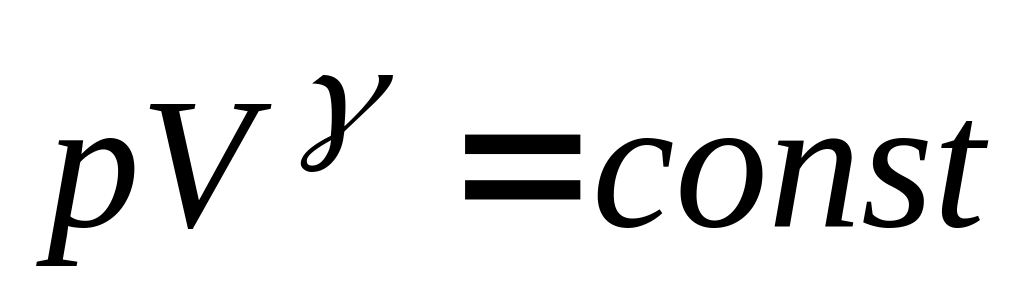
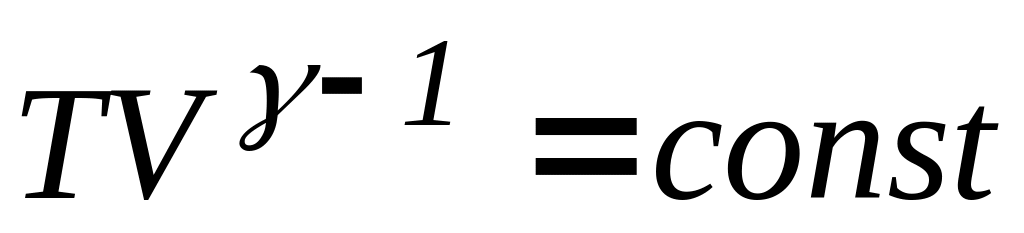
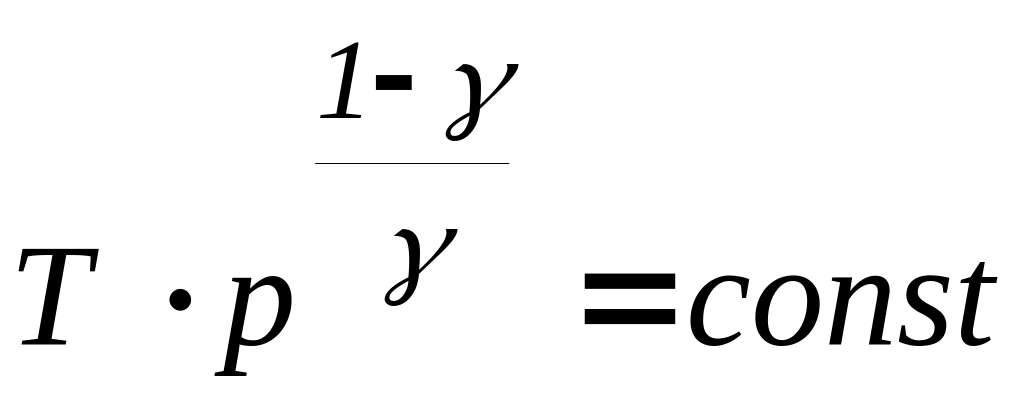
			(29)
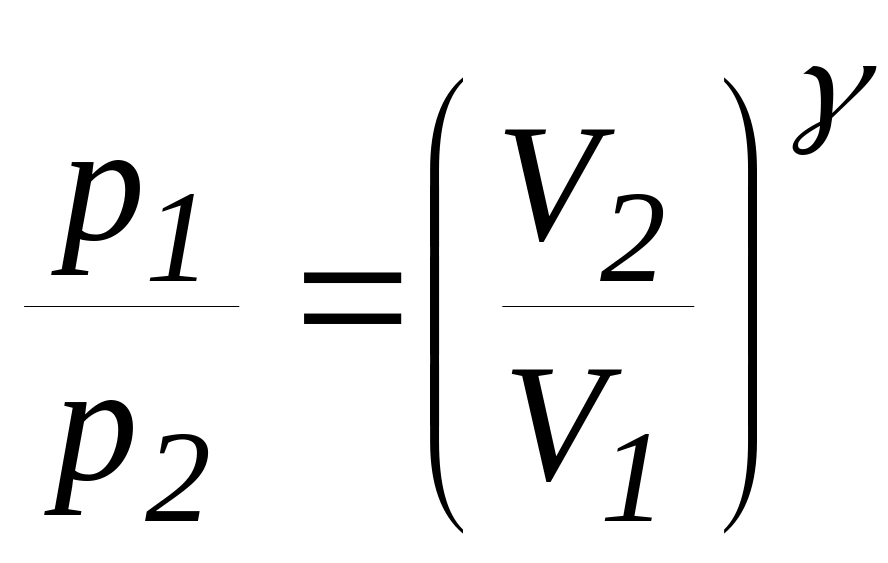
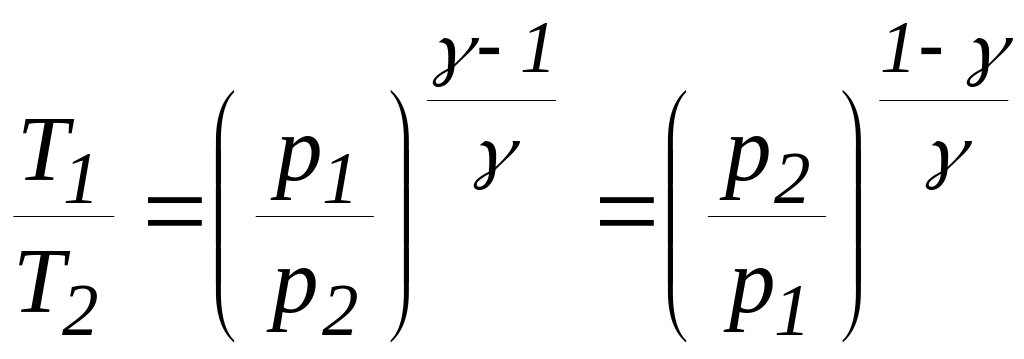
			(30)

Показник ступеню називають показником адіабати або показником Пуассона, він представляє собою відношення теплоємностей і , отже

= . (31)

Роботу, яку виконує газ при адіабатному переході із стану 1, що характеризують параметри ( p₁,V₁,T₁) до стану 2 з параметрами ( p₂,V₂,T₂ ) можна знайти по одній з трьох формул

=

(32)

Застосування першого закону термодинаміки для адіабатних процесів. Звернемо увагу, що для адіабатного процесу = 0, тому вираз (18) можна переписати у вигляді

– зростання внутрішньої енергії газу в адіабатному процесі можливо тільки внаслідок роботи зовнішніх сил по стисненню газу;

– робота розширення ідеального газу виконується за рахунок його внутрішньої енергії і завжди супроводжується зменшенням його температури. (Підкреслимо, що при розширенні ідеального газу в пустоту робота не виконується і в адіабатному процесі зменшення температури газу не відбувається).

Теплоємність адіабатного процесу дорівнює нулю.