27

7. Основи молекулярно-кінетичної теорії ідеальних газів.

7.1. Рівняння стану ідеальних газів.

Рівняння, що зв’язує – об’єм, – абсолютну температуру та – тиск газу, називають рівнянням стану. Для ідеальних газів рівняння стану Менделєєва – Клапейрона має вигляд

, (1)

де – маса, – молярна маса газу, = 8.31 Дж/моль - газова стала (універсальна фізична стала). Відношення = ν має назву кількості речовини і характеризує кількість молей газу. Кількість молекул в одному молі всіх газів однакова і дорівнює = 6,02∙10²³ 1/моль (число Авогадро – універсальна фізична стала). Для ν молей газу кількість молекул буде дорівнювати . Якщо газ складається з однакових молекул масою , то очевидно, що = .

Виходячи з того, що густина газу визначається як , з рівняння стану можна отримати значення при даних умовах

. (2)

Концентрація молекул = зв’язана з густиною газу співвідношенням . При цьому з рівняння стану (1) можна отримати вираз

, (3)

в якому введена величина = 1,38∙10^-23 Дж/К - стала Больцмана.

Для сумішей газів можна використовувати рівняння стану (1), поняття густини газу, концентрації молекул, молярної маси суміші. В основі їх коректного використання лежить закон Дальтона: тиск суміші газів дорівнює сумі їхніх парціальних тисків, тобто

. (4)

Парціальний тиск — це тиск, який чинить будь-яка з компонент суміші у відсутності усіх інших в тій самій посудині при тій самій температурі. Для знаходження молярної маси суміші треба використати визначення кількості речовини та врахувати адитивність маси і кількості речовини газу:

(5),

звідки знаходимо шукану молярну масу суміші μ_сум.

7.2. Ізопроцеси.

Перехід газу із стану 1, який характеризують параметри (p₁, V₁, T₁) до стану 2 з параметрами ( p₂,V₂,T₂ ) називають термодинамічним процесом. Якщо перехід 1–2 реалізують квазістатично, тобто через послідовність рівноважних станів, то процес є оборотним, і його можна представити графічно (Рис.1). Якщо при переході 1–2 один з параметрів (p, V, T) залишається сталим, то процеси називають ізотермічним ( = const), ізобарним ( = const), ізохорним ( = const).

Рівняння для кожного ізопроцесу можна записати в одному з двох виглядів:

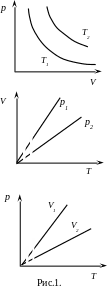
Ізотермічний ( =const)			(6)
ізобарний ( =const)			(7)
ізохорний ( =const)			(8)

Значення сталих (соnst₁ , соnst₂ , соnst₃) визначаються з рівняння стану (1).

Для ізотермічних процесів збільшення температури веде до зростання сталої соnst₁ і графіки, що відповідають приведеним функціям при ( ), показані на рис.1. а.

В рівнянні ізобарного процесу стала соnst₂ обернено пропорційно залежить від тиску. Тому при зростанні цього параметру ( ) кут нахилу прямої зменшується (рис.1, б).

В рівнянні ізохорного процесу стала соnst₃ обернено пропорційно залежить від об’єму, тому збільшення об’єму веде до зменшення кута нахилу прямої ( рис.1, в).

Відповідні залежності, показані в таблиці, мають назви законів: Бойля-Маріотта (ізотермічний процес), Гей-Люссака (ізобарний процес), Шарля (ізохорний процес).