Вопрос1
Опр.
1: Если любой
точке
,
принадлежащей области
комплексной плоскости
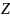по некоторому закону поставлено в
соответствие определённое значение
, то говорят, что в области задана
однозначная функция
.
Таким образом любую комплексную функцию
можно задать с помощью двух действительный
функций
и
.
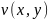Предел ФКП.
Непрерывность ФКП.
Пусть
– однозначная функция. Говорят, что
функция стремится к пределу
,
когда
, если существует сколь угодно много
,
,
то для всех
,
удовлетворяющих неравенству
,
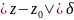будут выполняться следующие условия
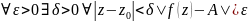. Опр.
2:
Функция
называется
непрерывной в точке
,
если её предел равен значению функции
в этой точке. Бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.Опр.
3:
Функция
называется
непрерывной в любой точке этой области
,
если она непрерывна в любой точке этой
области.
Вопрос4
Дифференцирование
ФКП. Условие Коши-Римана. Опр.
1: Производной
функции
в
произвольной точке
называется конечный предел разности
отношения
.
бесконечным
числом способов и производная не зависит
от способа стремления. Из дифференцируемости
функции
в некоторой точке следует её непрерывность
в этой точке. (поскольку
будет представлять конечные значения
(при
)
при
,
а это как раз и означает непрерывности
функции). Обратное утверждение в общем
случае неверно. Поскольку функция
может быть задана в виде суммы двух
действительных функций
и
,
то
любым образом накладывает на эти функции
u
и v
определённые условия, называемые
условиями Коши-Римана или Даламбера-Эйлера.
Вопрос5
Аналитические функции. Геометрический смысл модуля и аргумента производной. Конформные преобразования.
Опр.
1: Однозначная
функция
называется
аналитической в точке
,
если она является дифференцированной
(т.е. выполняются условия Коши-Римана)
не только в самой точке, но и в её
окрестности. Если функция является
аналитической в каждой точке некоторой
функции
,
то она является аналитической во всей
области.
Опр.
2: В точках
плоскости, в которых однозначная
функция
является
аналитической, называются правильными
точками. Точки, в которых функция не
является аналитической, называются
особыми. Пусть известно, что функция
является аналитической в точке
,
следовательно будет существовать
производная
;
,
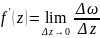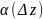–более
малого порядка.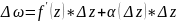
,
где
–главная
часть приращения функции. Опр.
3: Дифференциалом
аналитической функции
в
точке
называется главная часть приращения
функции.
,
так как
Вопрос6
геометрический
смысл модуля производной.
Величина
определяет коэффициент растяжения(сжатия)
в точке
при отображении
.
представляет собой предел отношения
бесконечно малого расстояния между
отображаемыми точками .
аргумент
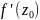представляет
собой угол междуотображаемым и
первоначальным направлениями касательных
к кривым
и
..
Т.е если мы отобразим 2ве касательные
на одном графике … Это и есть геометрический
смысл аргумента производной.
:Отображение
обладающее свойством сохранения углов
и постоянства растяжений в точке
называется конформным. Если при конформном
отображении сохраняется направление
отсчета углов, то она называется
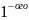рода, а если противоположно, то
рода. Т. О. если функция является
аналитической в точке
и
её производная в этой точке отлична от
0, то отображение
в данной точке
будет являться конформным.