5.2.5 Разработка алгоритма бесплатформенной инерциальной навигационной системы

Применение в качестве информационной системы рассматриваемого объекта БИНС, обуславливается преимуществами, присущими этому классу систем. К ним, прежде всего, следует отнести:

-отсутствие в этих системах такого сложного и дорогостоящего устройства, каким является гиростабилизированная платформа, являющаяся одним из основных элементов платформенных ИНС;

-меньшие массогабаритные характеристики и меньшее энергопотребление;

-более высокие надежностные характеристики.

Одним из основных вопросов, возникающих при разработке этих систем, является вопрос построения алгоритмов определения ими параметров движения объекта и алгоритма решения задачи начальной выставки этих систем.

Решение этой задачи обычно осуществляется в следующей последовательности. Сначала строится функциональный алгоритм, учитывающий лишь специфику задач, решаемых разрабатываемой БИНС и особенности определяемой ею информации, а затем, на базе этого алгоритма, строится, так называемый, численный алгоритм, т. е. алгоритм, учитывающий специфику работы ЦВМ, а также специфику сигналов, получаемых с используемых в инерциальной системе измерительных элементов.

5.2.5.1 Разработка функционального алгоритма определения координат и скоростей объекта, а также углов курса, крена и тангажа

При построении алгоритмов функционирования БИНС, одним из важных вопросов является вопрос формирования алгоритма решения так называемой задачи ориентации, состоящей в определении матрицы направляющих косинусов между системой координатных осей выбранной в качестве базовой (обычно используемой для решения основного уравнения инерциальной навигации) и трехгранником "С" , образованным измерительными осями акселерометров и жестко связанным с объектом.

В принципе, построение этого алгоритма может быть осуществлено либо на основе использования уравнения Пуассона, либо на основе описания углового движения твердого тела с помощью таких кинематических параметров как углы Эйлера, параметры Родрига-Гамильтона, являющиеся компонентами кватерниона, вектор истинного поворота и другие.

Сравнительная оценка этих способов как с точки зрения объема вычислений, выполняемого при их реализации в БЦВМ, так и с позиции получения наилучшей точности решения задачи ориентации, показала, что для решения этой задачи наиболее предпочтительным является использование параметров Родрига-Гамильтона, поскольку их использование требует решение системы дифференциальных уравнений лишь четвертого порядка (в то время как применение уравнений Пуассона требует решение системы дифференциальных уравнений девятого порядка) а также минимизирует влияние так называемых ошибок масштаба.

Анализ различных способов построения алгоритма определения параметров движения объекта показал, что в качестве базового трехгранника-трехгранника используемого для решения основного уравнения инерциальной навигации, в рассматриваемой системе наиболее целесообразно использовать горизонтный трехгранник "Г" , ось которого ориентирована по текущей вертикали, а оси и соответственно на Восток и Север.

Учитывая, что рассматриваемая система должна определять сферические координаты: географическую широту и долготу местоположения объекта, северную и восточную составляющие его путевой скорости, а также углы курса , тангажа и крена , алгоритм решения основного уравнения инерциальной навигации целесообразно построить следующим образом.

Воспользовавшись соотношением

, (5.2.1)

устанавливающим связь между скоростью движения объекта относительно Земли и его абсолютной скоростью , где геоцентрический радиус-вектор центра масс объекта, а вектор угловой скорости вращения Земли, основное уравнение инерциальной навигации можно записать в виде

. (5.2.2)

Учитывая, что вектор ускорения силы тяжести

,

последнее уравнение можно записать и так

, (5.2.3)

или представить в интегральной форме записи

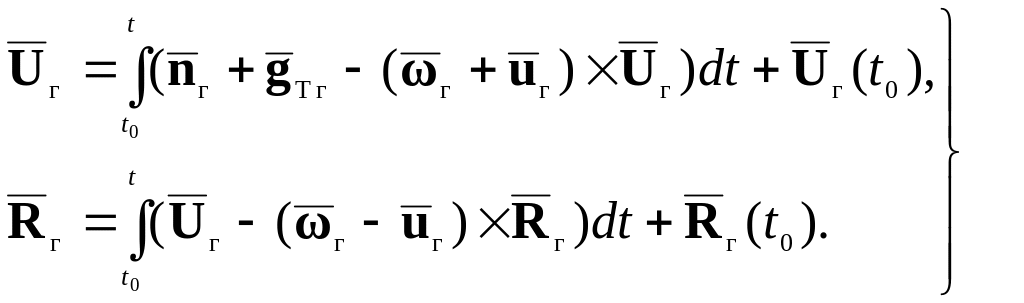(5.2.4)

В этих уравнениях , , - вектор напряженности поля тяготения Земли, - вектор абсолютной угловой скорости вращения горизонтного трехгранника, а - вектор кажущегося ускорения. Символом «∙», поставленными над вектором , обозначена локальная производная, т. е. производная, взятая во вращающемся базисе . Следует заметить, что все переменные этих уравнений являются функциями времени t. Однако для сокращения записи и упрощения дальнейшего изложения этот аргумент в дальнейшем записывать не будем.

В проекциях на оси и горизонтного базиса уравнение (5.2.4), определяющее алгоритм вычисления компонент путевой скорости и , примет вид

(5.2.5)

В этом алгоритме исключен канал определения высоты и вертикальной скорости движения объекта в силу того, что, как известно, ошибки функционирования этого канала носят нарастающий с течением времени характер. При этом, необходимые для работы инерциальной системы, данные о высоте и вертикальной скорости, должны определяться с помощью сторонних измерителей, например, с помощью барометрических измерителей.

Входящие в эти уравнения компоненты вектора абсолютной угловой скорости вращения горизонтного трехгранника , , и величины , могут быть вычислены с помощью следующих соотношений

(5.2.6)

где через

и (5.2.7)

обозначены компоненты вектора угловой скорости вращения этого трехгранника относительно Земли.

Процедура вычислений радиусов кривизны меридионального сечения земного эллипсоида и его сечения плоскостью первого вертикала определяется следующими соотношениями

, (5.2.8)

где и представляют собой квадрат первого эксцентриситета и большую полуось земного эллипсоида.

Информацию о компонентах вектора кажущегося ускорения и , необходимую для решения уравнений (5.2.5), можно получить путем пересчета компонент этого вектора , и измеренных в базисе блоком акселерометров, с помощью матрицы направляющих косинусов

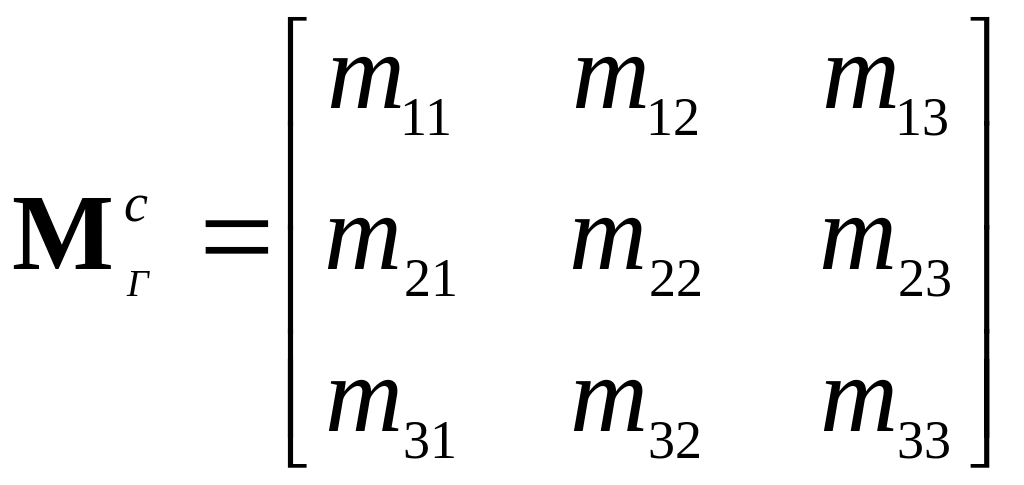, (5.2.9)

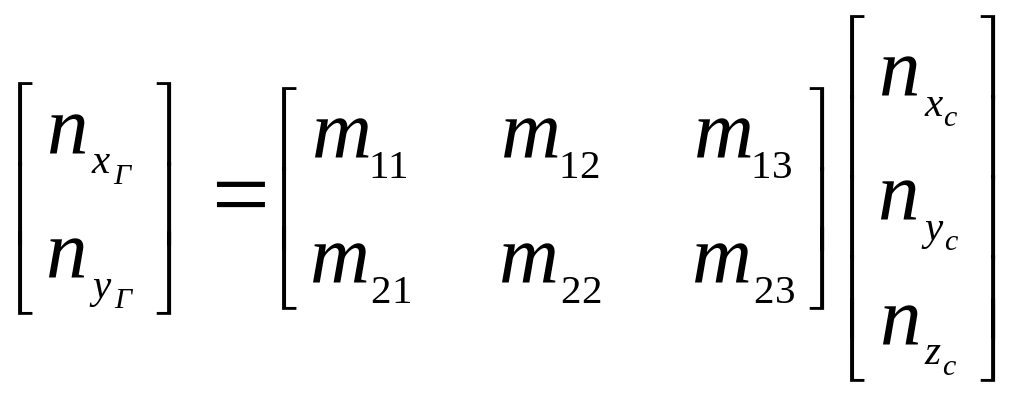. (5.2.10)

Вычисление матрицы может быть осуществлено по вектору относительной угловой скорости вращения трехгранников и . Компоненты этого вектора можно найти с помощью следующего соотношения

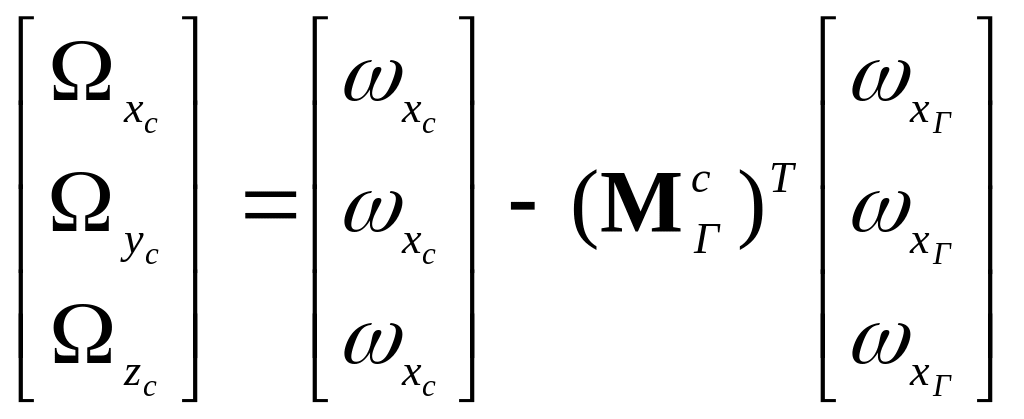. (5.2.11)

Входящие в это уравнения величины , , измеряются с помощью трех датчиков угловой скорости, измерительные оси которых совпадают с осями базиса , а угловые скорости , , вычисляются по соотношениям (5.2.6).

Среди существующих способов вычисления матрицы направляющих , с точки зрения их использования при построении алгоритмов БИНС, наиболее целесообразным является применение способа, базирующегося на описании взаимной ориентации двух базисов с помощью параметров Родрига-Гамильтона. В этом случае алгоритм вычисления этой матрицы будет содержать систему дифференциальных уравнений

(5.2.12)

определяющую процедуру вычисления самих параметров Родрига-Гамиль-тона , , , по информации о компонентах вектора угловой скорости и выражений, описывающих процедуру вычисления по этим параметрам элементов матрицы

, , ,

, , ,

, , .

При вычислении элементов кватерниона ориентации по уравнениям (5.2.12) его норма , из-за ошибок вычислений, может отличаться от единицы, что приведет к ошибке вычисления матрицы . Для компенсации этой ошибки в алгоритмах такого типа обычно применяется процедура коррекции нормы кватерниона, т. е. приведения ее к единице.

Алгоритм с коррекцией нормы можно представить в следующем виде

(5.2.13)

При использовании этого алгоритма норма кватерниона всегда будет равна единице.

Начальные значения параметров Родрига-Гамильтона , , , для решения системы дифференциальных уравнений (5.13) можно определить по формулам

(5.2.14)

где через обозначены значения элементов матрицы , определенной в процессе начальной выставки БИНС.

Располагая информацией об элементах матрицы , можно определить значения углов курса , тангажа и крена . Выбрав в качестве последовательности поворотов трехгранника относительно базиса последовательность , эту матрицу можно записать так

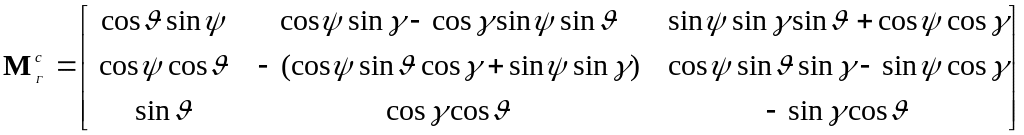(5.2.15)

В этом случае алгоритм вычисления углов , и нетрудно представить в виде

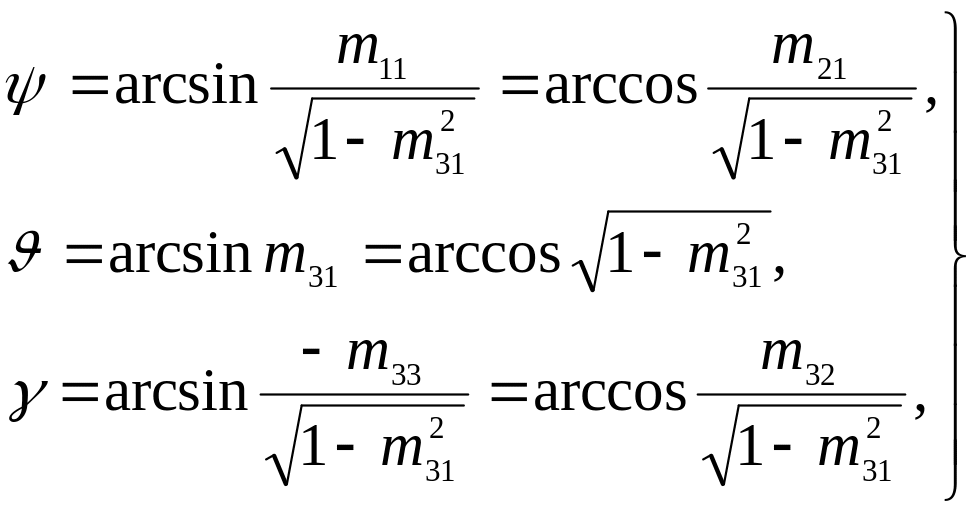(5.2.16)

либо, учитывая связь между функциями и параметрами Родрига-Гамильтона , , , , описать соотношениями

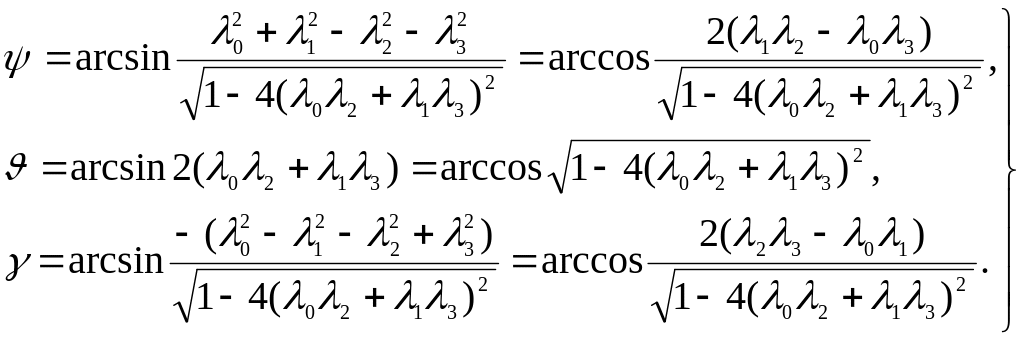(5.2.17)

Следующей задачей, которую должна решать БИНС, является задача определения текущих координат объекта и . Их можно вычислить двумя способами. В первом значения этих координат определяются путем интегрирования компонент вектора угловой скорости вращения трехгранника относительно Земли и

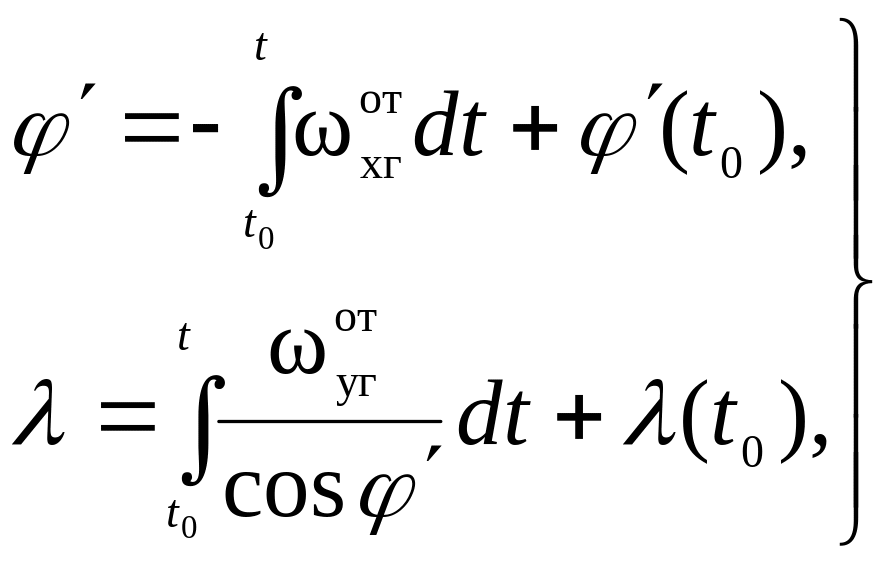(5.2.18)

а, во втором, они могут быть вычислены через элементы матрицы

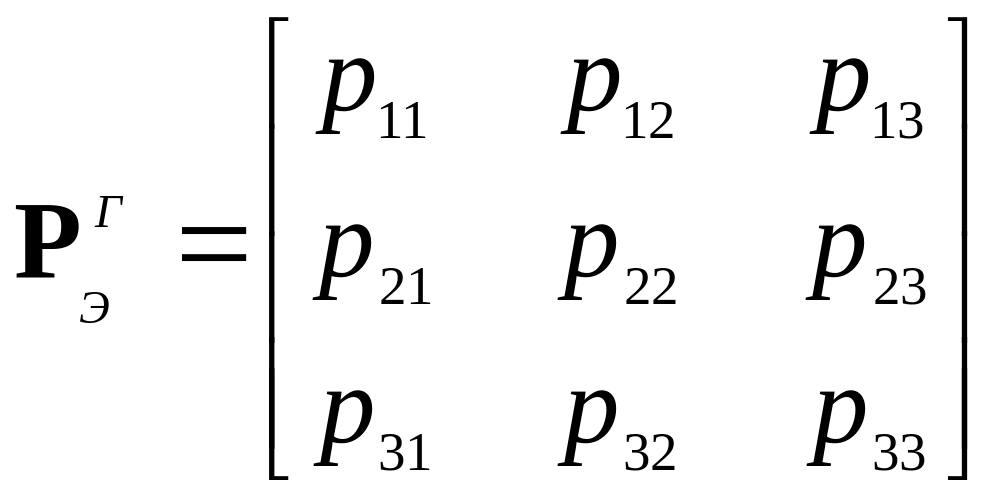, (5.2.19)

описывающей ориентацию трехгранника относительно жестко связанного с Землей экваториального базиса "Э" , ось которого направлена по линии пересечения плоскости гринвичского меридиана и плоскости экватора, а ось по оси вращения Земли.

Элементы этой матрицы можно выразить через координаты текущего местоположения объекта следующим образом

. (5.2.20)

Поскольку трехгранник вращается относительно Земли с угловыми скоростями , и , алгоритм вычисления матрицы можно представить в виде системы дифференциальных уравнений

(5.2.21)

определяющих процедуру вычисления по этим угловым скоростям параметров Родрига-Гамильтона и выражений, описывающих алгоритм нахождения по этим параметрам элементов этой матрицы

, , ,

, , ,

, , .

Начальные значения параметров Родрига-Гамильтона для решения системы дифференциальных уравнений (5.21) можно определить по начальной матрице , выраженной через координаты точки старта и

, (5.2.22)

с помощью следующих соотношений

(5.2.23)

Для построения алгоритма вычисления текущих координат объекта и воспользуемся матрицей (5.2.20). Из нее следует, что текущие координаты объекта могут быть определены с помощью следующих соотношений

(5.2.24)

. (5.2.25)

Полученные выше соотношения образуют функциональный алгоритм решения в БИНС как навигационной задачи, так и задачи ориентации. Однако при построении этого алгоритма не учитывались способы и особенности его практической реализации. В связи с тем, что он должен быть реализован в ЭВМ, возникает задача построения на его базе, так называемого, численного алгоритма, - алгоритма, учитывающего специфику и особенности функционирования этих устройств.