4. Система смешанного типа с ограничением по длине очереди

В системах обслуживания смешанного типа с ограничением по длине очереди заявка, заставшая все каналы занятыми, становится в очередь лишь в том случае, если ее длина не превышает некоторого . Если же число заявок в очереди уже равно , то вновь поступившая заявка покидает систему необслуженной.

Рассмотрим такую n-канальную систему обслуживания, сохранив прежние допущения о том, что входящий поток заявок простейший и время обслуживания распределено по показательному закону.

Число возможных состояний такой системы конечно, так как общее число заявок, связанных с системой в этом случае не может превышать . Перечислим эти состояния

все каналы свободны, очереди нет;

занят ровно один канал, очереди нет;

^{………………………………………………………………………}

занято ровно k каналов, очереди нет;

^{………………………………………………………………………}

заняты все n каналов, очереди нет;

заняты все n каналов, одна заявка стоит в очереди;

^{……………………………………………………………………}

заняты все n каналов, s заявок стоят в очереди;

^{……………………………………………………………………}

заняты все n каналов, q заявок стоят в очереди.

Поскольку число возможных состояний системы конечно и каждое из них достижимо из любого другого, предельный вектор в такой системе существует. Заметим, кроме того, что в такой системе обслуживания заявка, занявшая очередь, будет ожидать обслуживания неограниченно долго. Это обстоятельство позволяет использовать для описания процесса функционирования такой системы первые уравнений, полученных для смешанной системы обслуживания с ограничением по длительности, считая при этом параметр .

Соответствующая совокупность алгебраических уравнений имеет вид

Особенность структуры последнего уравнения связана, во-первых, с тем, что поступление нового требования в момент, когда система находится в состоянии , не может изменить состояния системы, а, во-вторых, с тем, что состояние является крайним и поэтому переход из в невозможен.

Решая так же, как и ранее, эту систему уравнений с привлечением дополнительного условия

,

Окончательно получим

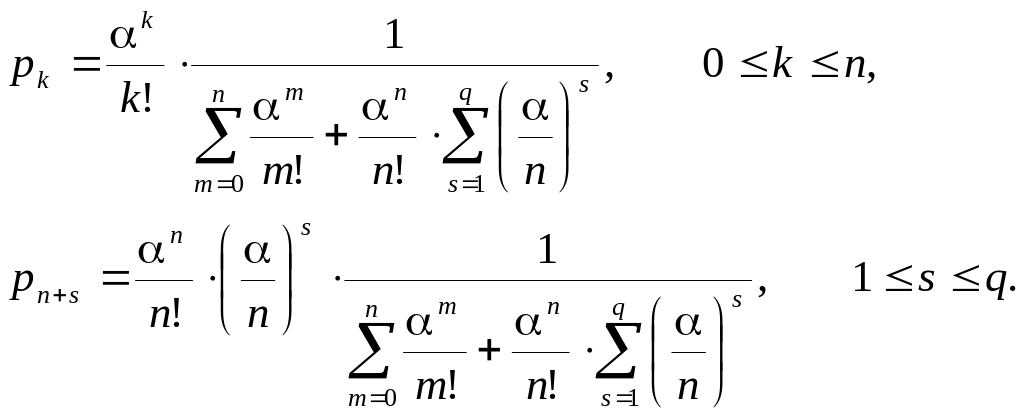
Вероятность того, что заявка покинет систему необслуженной, равна вероятности того, что в очереди уже стоит заявок. Нетрудно заметить, что эти формулы могут быть получены из формул анализа поведения СМО с ожиданием, если положить в них и ограничить суммирование по верхней границей .

Пример. В двухканальную систему массового обслуживания поступает поток заявок с плотностью . Среднее время обслуживания одной заявки . Допустимая длина очереди равна 3. Рассчитать вероятность отказа, среднее число заявок в очереди, среднее время ожидания в очереди.

Решение

По формуле находим

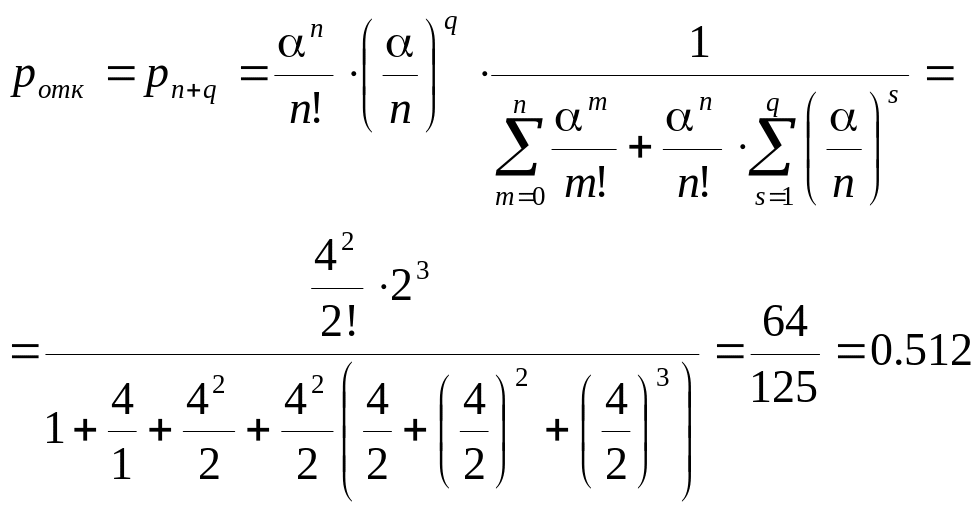
Среднее число заявок в очереди рассчитывается по формуле

Наконец, среднее время ожидания начала обслуживания для заявки, вставшей в очередь:

5. Система смешанного типа с ограничением по длине очереди

6. Анализ многофазных смо

Процесс функционирования таких СМО протекает следующим образом: заявка в ходе обслуживания проходит последовательно несколько фаз обслуживания, выполняемых различными аппаратами.

Рассмотрим 2-фазную СМО, функционирование которой организовано следующим образом:

Заявка поступает на вход первой фазы, представляющей собой одноканальную СМО с ожиданием и ограничением по длине очереди. Если канал свободен, начинается обслуживание, в противном случае заявка становится в очередь, если она не превышает предельно допустимую , и ждет начала обслуживания случайное время , распределенное в соответствии с

где среднее число заявок, покидающих очередь в единицу времени, причем ;

среднее значение продолжительности ожидания начала обслуживания.

Обслуженная первой фазой заявка поступает во вторую фазу, представляющую собой канальную СМО без потерь. Будем считать, кроме того, что в системе действует эффект «блокировки», проявляющийся в том, что первая фаза не принимает заявок на обслуживание, даже если ее канал свободен, когда заняты все каналы второй фазы. Пусть на вход СМО поступает простейший поток с интенсивностью , а интенсивности обслуживания для первой и второй фаз соответственно равны и .

Введем множество возможных состояний системы. Каждому состоянию системы поставим в соответствие пару чисел , где количество заявок, связанных с первой фазой системы (оно равно сумме числа обслуживаемых и находящихся в очереди заявок), число заявок, обслуживаемых второй фазой.

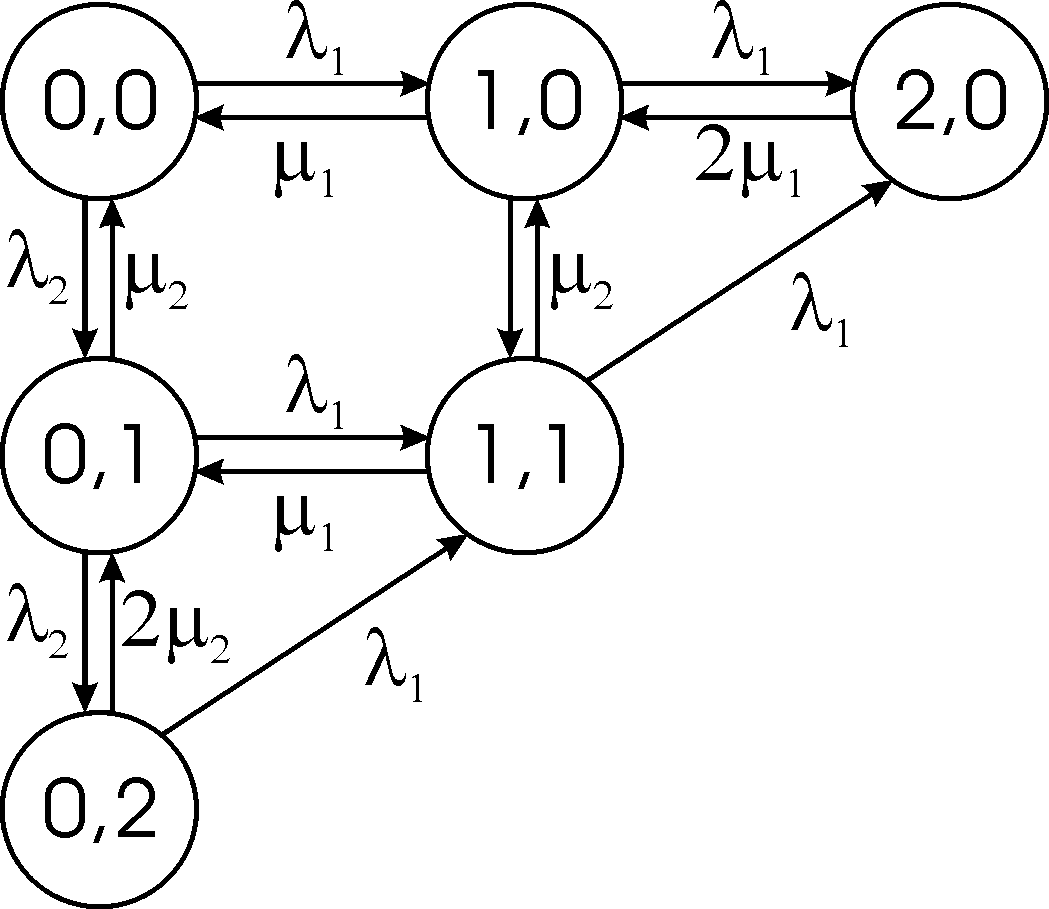
Изобразим граф состояний и переходов системы для случая, когда , а максимальная длина очереди (рис). Эффект «блокировки» сказывается здесь следующим образом: если (оба канала второй фазы заняты), то все заявки, связанные с первой фазой, находятся в очереди.

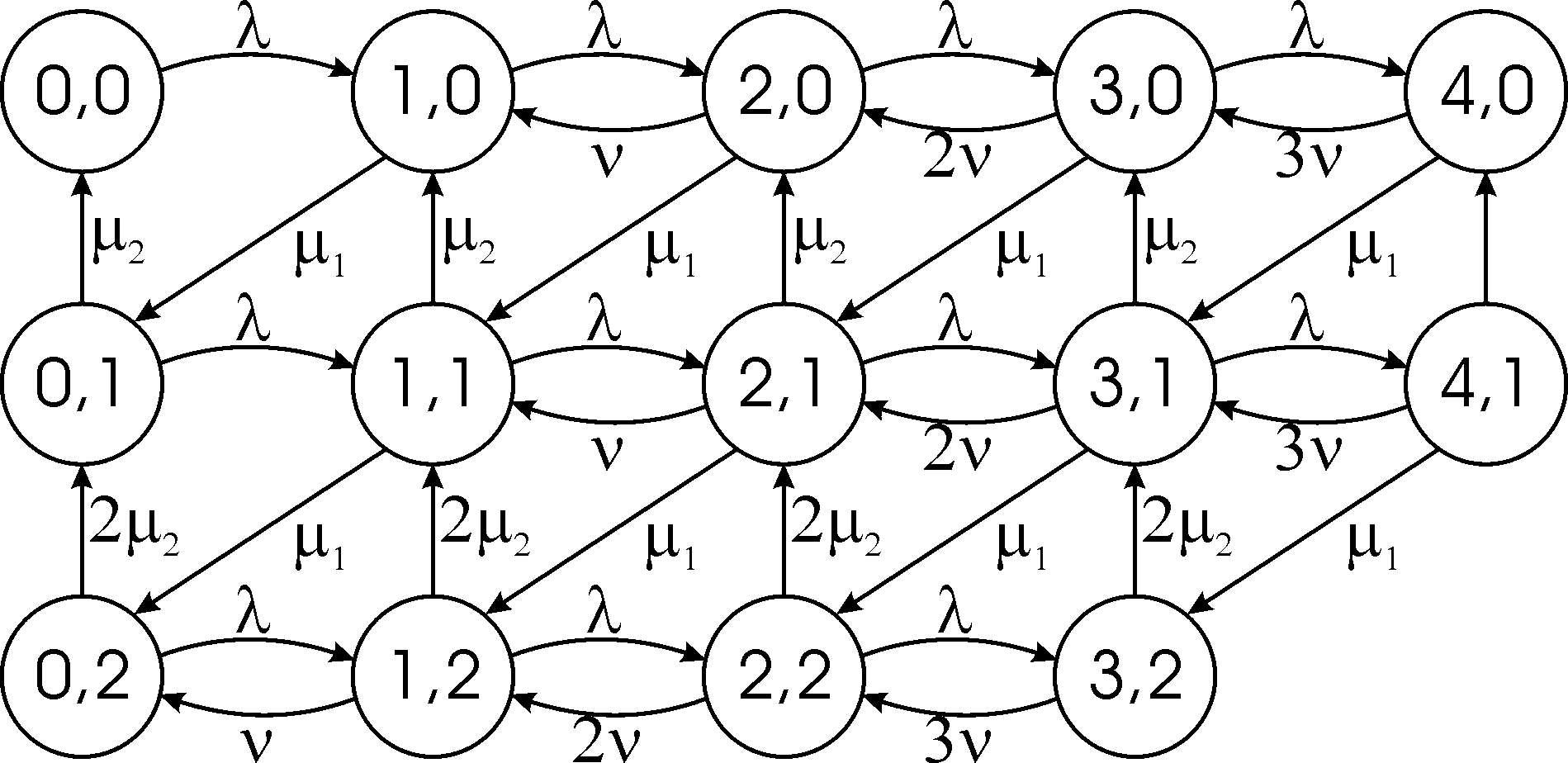
Действуя в соответствии с общей методикой, запишем систему уравнений относительно финальных вероятностей системы.

Решение системы дает искомый набор вероятностей С использованием этого набора определим некоторые показатели эффективности системы. Для оценки пропускной способности системы рассчитаем среднее число заявок, обслуживаемых системой в единицу времени, равное

,

где среднее число занятых обслуживанием каналов второй фазы.

.

Тогда средняя доля обслуженных заявок определяется отношением .

Вероятность блокировки

.

Ясно, что в рамках Марковских моделей аналогичным образом может быть проведен анализ и более сложных многофазных систем.