IV.Частотные передаточные функции, установление устойчивости по частотному критерию.
Теоретические основы
С помощью преобразования wplane, мы можем исследовать устойчивость импульсных систем по ИПФ в пространстве w по критериям, разработанным для линейных непрерывных систем.
Воспользовавшись критерием Найквиста, определим устойчивость систем, замкнутых отрицательной обратной связью.
Критерий Найквиста позволяет установить устойчивость системы, охваченной отрицательной обратной связью, (замкнутой системы) по частотной передаточной функции разомкнутой системы.
Критерий Найквиста: пусть
W(s)=P(s)/Q(s) -правильная дробь, многочлены
P(s) и Q(s) не имеют совпадающих корней в
правой полуплоскости, число полюсов
W(s) в правой полуплоскости "
",
тогда для устойчивости замкнутой системы
необходимо и достаточно, чтобы при
изменении
от 0 до
,
годограф
охватывал точку ( -1,0 ) на угол
.
Другими словами, для устойчивости
замкнутой системы необходимо и достаточно,
чтобы угол поворота годографа Hраз(jw)
относительно точки (-1, 0) равнялся πL, где
L – количество строго неустойчивых
корней знаменателя Hраз(iw).
Геометрическое правило Цыпкина: Для устойчивости замкнутой системы необходимо и достаточно, чтобы число пересечений годографа Hраз(jw) вещественной оси ReHраз(jw) левее точки (-1, 0) равнялось бы L/2, где L – количество строго неустойчивых корней знаменателя Hраз(iw).
Опыт
А) T=0.01 par1=0.1
T=0.01
par1=0.1
w1=2/(s+18)
w2=4/ ( par1*s^2+5*s+7 )
w3=4/ (s+2)
wnepr=w1*w2/(1+w2*w3)
wz_ch=convert(wnepr,8,T)
wz=wz_ch/ ( 1+wz_ch )
CC>wpl=wplane(wz)
CC>hobr=wpl/(1-wpl)
CC>pzf(hobr)
3,215e-06(w+2)(w-200)(w+316,2)(w-385)
hobr(w) = ———————————————————————————————————————
[(w+1,685)^2+1,825^2] (w+17,95)(w+47,69)
Таким образом мы имеем 0 корней в положительной области, т.о. чтобы разомкнутая система была устойчивая необходимо, чтобы годограф замкнутой не огибал точку (-1,0). Смотрим, что получилось:
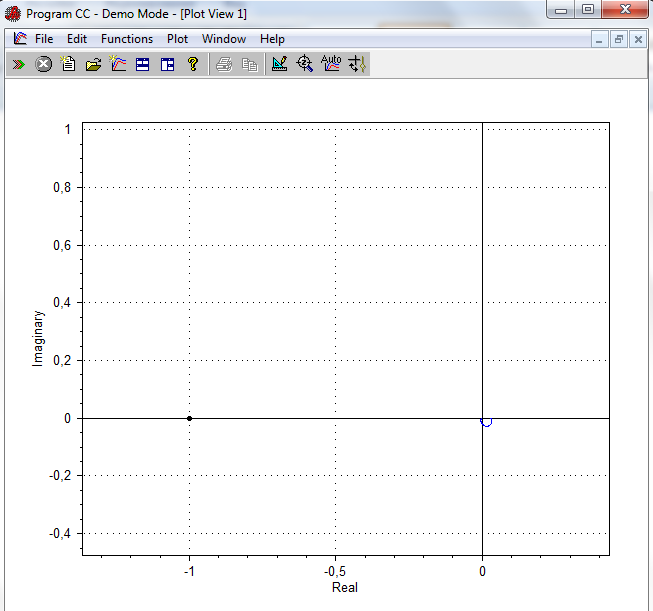
Так и получилось, система устойчива.
Б) T=10 par1=80
T=10
par1=80
w1=2/(s+18)
w2=4/ ( par1*s^2+5*s+7 )
w3=4/ (s+2)
wnepr=w1*w2/(1+w2*w3)
wz_ch=convert(wnepr,8,T)
wz=wz_ch/ ( 1+wz_ch )
wpl=wplane(wz)
hobr=wpl/(1-wpl)
pzf(hobr)
-0,005294(w+0,1998)(w-0,2)(w+0,2)(w+2,739)
hobr(w) = ———————————————————————————————————————————
(w+0,2)^2 [(w+0,02469)^2+0,3118^2]
Опять же получаем ситуацию аналогичную пункту а). у нас нет неустойчивых корней, поэтому для устойчивости разомкнутой необходимо неогибание годографом точки.
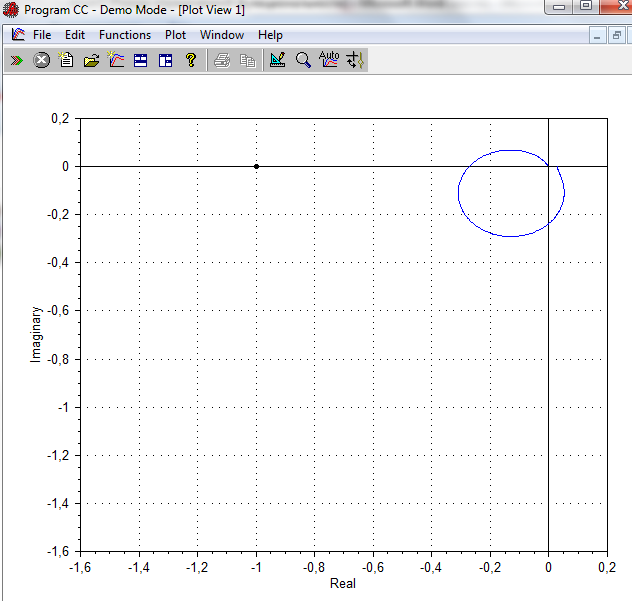
С-ма устойчива.
В) T=0.00001 par1=80
T=0.00001
par1=80
w1=2/(s+18)
w2=4/ ( par1*s^2+5*s+7 )
w3=4/ (s+2)
wnepr=w1*w2/(1+w2*w3)
wz_ch=convert(wnepr,8,T)
wz=wz_ch/ ( 1+wz_ch )
wpl=wplane(wz)
hobr=wpl/(1-wpl)
nyquist(hobr)
CC>pzf(wz)
-6,325e-18[(z+0,7551)^2+0,2172^2] (z-1)(z-6,054)
wz(z) = —————————————————————————————————————————————————
(z-0,9997)[(z-1)^2+0,0001648^2] (z-1)
CC>pzf(wpl)
-5,978e-19(w-3,213)(w-1,433e+05)[(w+7,14e+05)^2+8,109e+05^2]
wpl(w) = ————————————————————————————————————————————————————————
w(w+0,1161)(w+1,946)(w+18)
Годограф имеет вид:
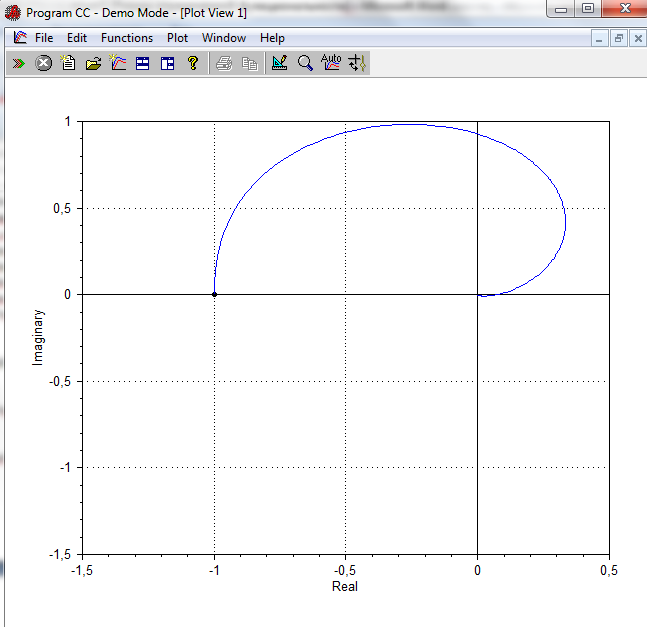
Мы видим ,что система находится на границе устойчивости(!!).Из вида wpl(w) (см. пред. с тр.) мы в этом конкретно убеждаемся.