С анкт-Петербургский Государственный

Политехнический Университет

Факультет Технической Кибернетики

Кафедра Информационных и Управляющих Систем

Лабораторная работа по «тау» №3 Тема: Анализ импульсных систем управления

Вар: 18.

Выполнил:

Матвеева Наталья

Группа :3084/1

2012

Цель работы:

Исследование особенностей импульсных САР.

Задачи работы:

1)построить передаточную функцию,

2)исследовать устойчивость "корневым" методом, построить область устойчивости по пара­метрам T и par1,

3) построить переходную функцию,

4)построить частотные передаточные функции, пользуясь частотными критериями устано­вить устойчивость системы,

5)построить отклик системы на заданное входное воздействие, при различных интервалах квантования - T .

Задание:

Из предыдущих лабораторных имеем:

Вид передаточных функций для звеньев:

,par1=1; par2=5

Входные воздействия:

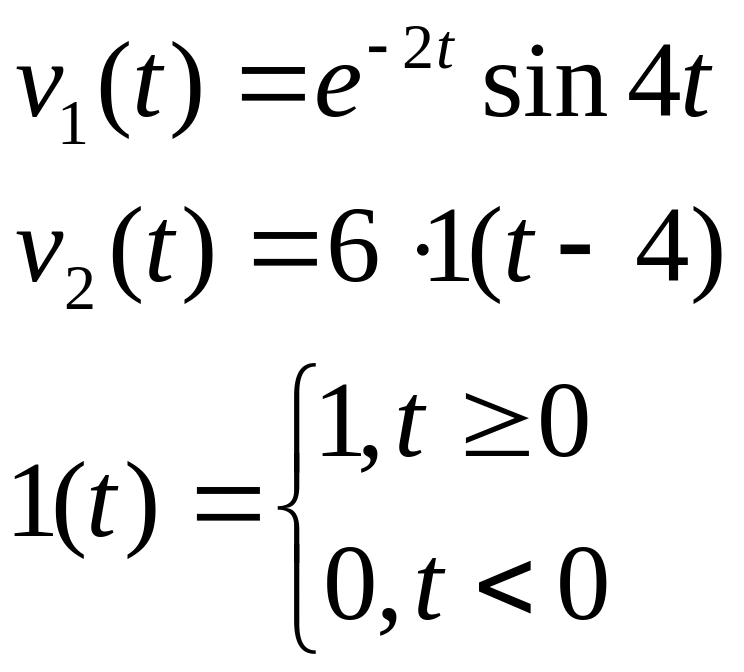
I.Построение передаточной функции.

Теоретические основы

Объектом рассмотрения данной лабораторной работы является импульсная САР. В ней сигнал в одной или нескольких точках квантуется во времени. Поэтому связь между элементами, разделенными квантователями, сущест­вует только в моменты выборки. В остальное время движение непрерывных элементов системы происходит под действием импульсных возмущений с выхода квантователя.

Можно выделить следующие типы квантоватилей:

• Амплитудно-импульсные модуляторы

Из непрерывного входного сигнала f(t) формируется последовательность прямоугольных импульсов f*(t) постоянной длительности p , следуют с постоянной частотой и амплитудой, равной значению сигнала в момент выборки

• Широтно-импульсные модуляторы

Формируют последовательности прямоугольных импульсов постоянной амплитуды с длительностью пропорциональной амплитуде входного сигнала в начале интервала квантования.

• Устройство выборки-хранения

Выбирает значение входного сигнала в момент времени t и сохраняет его не время T до очередного момента выборки. На практике представляет собой звено ЭОП(экстраполятор нулевого порядка) с ключом на входе.

• Аналого-цифровые преобразователи

После аналого-цифровых преобразо­вателей должны присутство­вать цифровые элементы обработки сигналов, а затем цифро-аналоговые преобразователи для согласования цифровых элементов с непрерывными.

Подобно непрерывным системам удобно использовать передаточные функции для описания импульсных систем. Для удобства математического описания импульсных систем вводят поня­тие идеального квантователя. В идеальном квантователе время выборки p меньше периода квантования T наименьшей постоянной времени входного сигнала f(t). Изображение по Лапласу его выхода имеет вид: (1.1) , а сам сигнал на выходе: (1.2).

Реальные квантователи могут быть представлены последовательным вклю­чением идеального квантователя и некой непрерывной системы: напри­мер, устройство выборки-хранения с запоминанием на интервал кванто­вания может быть представлен как идеальный квантователь и последовательно соединенный с ним экстраполятор нулевого порядка. Передаточная функция такого экстраполя­тора: (1.3)

Преобразование Лапласа сигнала с выхода идеального квантователя (дискретное преобра­зование Лапласа последовательности ) равно:

Если выполнить замену переменных , получим:

Это преобразование называют z-преобразованием.

Импульсная передаточная функция через обычную передаточную определяется как:

Правила преобразования структурных схем импульсных сис­тем:

1. Система содержит только импульсные элементы.

Операции преобразования структурных схем систем, содержащих квантователи на входе ка­ждого звена, выполняются по правилам преоб­разования непрерывных систем.

2. Смешанные системы.

Смешанные системы содержат и непрерывные и импульсные элементы. При составлении импульсной передаточной функции смешанной системы записывают импульсные передаточные функции отдельных блоков. Деление на блоки производится по правилу "от ключа до ключа". Клю­чом в системе является квантователь. Кроме того считается, что на выходе действуют фик­тивный идеальный квантова­тель .

Опыт

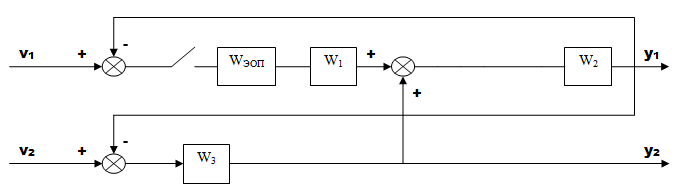
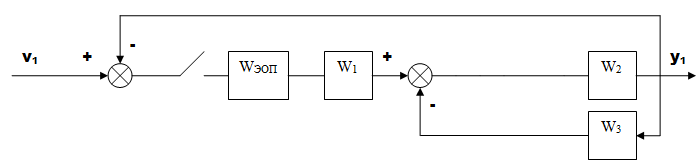
Найдем импульсную переходную функцию системы от первого входа к первому выходу:

Добавим на выходе фиктивный ключ (2):

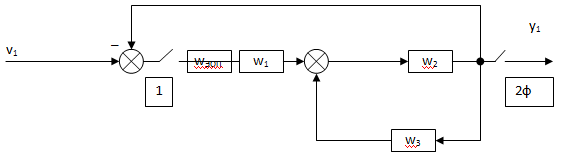
Делим на 2 блока:

А) Прямая цепь (ключ1-ключ2). Этот блок составляют 4 непрерывных звена: w_{эоп ,}w_1, w_2, w_3.

ИПФ, соответствующая этим последовательно со­единенным звеньям, равна:

WэопW1W2W3 (z)= z{ ilt( Wэоп(s) *W1(s) *W2(s) / ( 1+W2(s)W3(s) ) ) }

Б)Обратная связь (ключ 1-ключ 1) . Этот блок также составляют 5 непрерывных звенен: w_{эоп ,}w_1, w_2, w_3, 1(на обратной связи)

ИПФ, соответствующая этим последовательно со­единенным звеньям, равна:

WэопW1W2W3*1 (z)= z{ ilt( Wэоп(s) *W1(s) *W2(s) / ( 1+W2(s)W3(s) ) ) }

Тогда финальная ИПФ будет иметь вид:

W (z)= WэопW1W2W3 (z) / (1+ WэопW1W2W3 (z) )

В системе CC промоделируем систему с определенными параметрами. В СС z-преобразование сигнала, имеющего изображение по Лапласу Gi получают по команде 'convert'. Эта команда имеет различные варианты приближен­ного и точного выполне­ния такого преобразования. Точное преобразова­ние производится при задании параметра в разделе "тип дискретизации" равным 7, а при задании па­раметра равным 8.

У нас par1=1; T=0,01.

CC>T=0.01

CC>w1=2/(s+18)

CC>w2=4/ ( s^2+5*s+7 )

CC>w3=4/ (s+2)

CC>wnepr=w1*w2/(1+w2*w3)

CC>wz_ch=convert(wnepr,8,T)

CC>wz=wz_ch/ ( 1+wz_ch )

CC>display(wz)

6,168e-18(z^4 +2,042e+11z^3 +5,714e+11z^2 -5,742e+11z -1,784e+11)

wz(z) = —————————————————————————————————————————

z^4 -3,766z^3 +5,311z^2 -3,324z +0,7788