Литература
1. К.Хамахер, З.Вранешич. Организация ЭВМ. Москва 2003г.
2. Гук М. Энциклопедия: Аппаратные средства IBM PC. Санкт-Петербург 2000 г.
3. Джон Гудмен. Секреты жесткого диска. Москва. 1998
4. Уинн Л. Рош. Библия по техническому обеспечению. Минск МХХК "Динамо" 1995 г
5. Скотт Мюллер. Модернизация и ремонт IBM PC. Москва 2001г.
6. А.Пилгрим. Персональный компьютер модернизация и ремонт. Книга 2. Дюссельдорф- Киев- Москва-Санкт-Петербург. 2000 г.
Дисциплина «Теория автоматического управления»
1. Структура системы автоматического управления. Классификация САУ и задачи, которые они решают.
2. Связь входа и выхода. Способы построения моделей. Переходная функция и импульсная характеристика.
3. Понятие передаточной функции. Преобразования Лапласа.
4. Типовые звенья линейных систем (усилитель, апериодическое звено, интегрирующее звено, колебательное звено, звено запаздывания).
5. Частотные характеристики. Понятие ЛАЧХ и ЛФЧХ.
6. Логарифмические частотные характеристики типовых линейных звеньев.
7. Структурные схемы и правила их преобразования.
8. Требования к системам автоматического управления (перечислить). Понятие точности управления.
9. Частотные критерии устойчивости. Критерий Найквиста.
10. Алгебраические критерии устойчивости. Критерий Гурвица. Критерий Вишнеградского.
11. Оценка качества системы. Запасы устойчивости.
12. Синтез регуляторов. Задачи синтеза.
13. Синтез линейны непрерывных САУ. Коррекция САУ.
14. Разновидности и свойства САУ в зависимости от параметров синтеза.
15. Приведение задач ТАУ к нулевым начальным условиям. Линеаризация математического описания системы.
16. Математические модели. Способы их построения. Линейность и нелинейность систем и моделей.
17. Преобразование произвольного сигнала линейным звеном.
18. Интегральные оценки качества переходных процессов: линейные, квадратичные.
19. Типовые линейные законы регулирования. Виды регуляторов.
20. Расчет оптимальных параметров настройки регуляторов.
Примеры заданий:
1
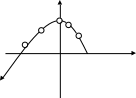
Аналитически определить выходной сигнал 3с после поступления на вход сигнала X(t)=10 (t). Получите график переходного процесса на модели и сравните полученные результаты.
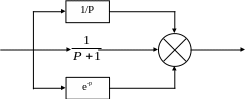W1
X(t) W2 + Y(t)
W1
Передаточная функция на выходе системы:
О
ригинал
от изображения Лапласа:
X(t) Y(t)
2
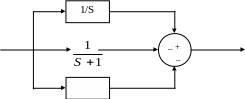
Аналитически определить угол сдвига фазы сигнала Y(t) в установившемся режиме, если на входе действует сигнал X(t)=sinωt, где ω=1с-1 . С помощью пакета программ постройте графики АЧХ и ФЧХ. Подтвердите полученный результат.
X(t) ε(t) Y(t)
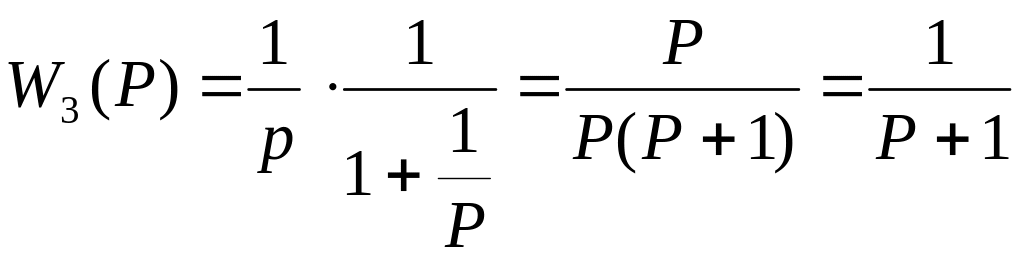Передаточная
функция замкнутой системы
Изображение
Лапласа
Y
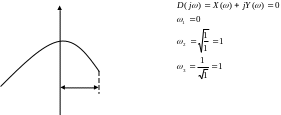
ω2
ω1 =0 X
ω3 K
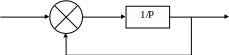
3
Запишите
выражение для модуля комплексного
коэффициента усиления. С помощью пакета
программ постройте АЧХ для приведённой
цепочки двух последовательно соединенных
звеньев с передаточной функцией.
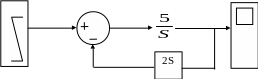
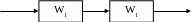X(t)
Y(t)
Передаточная функция системы
A(ω)
50
ω
5
4
На вход звеньев поступает сигнал X(t)=1(t). Аналитически определите значение выходного сигнала Y(t) через 0,1с после поступления сигнала на вход и подтвердите полученный результат путём моделирования приведенной системы.
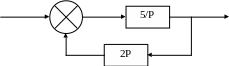
X(t) Y(t)
Передаточная функция системы
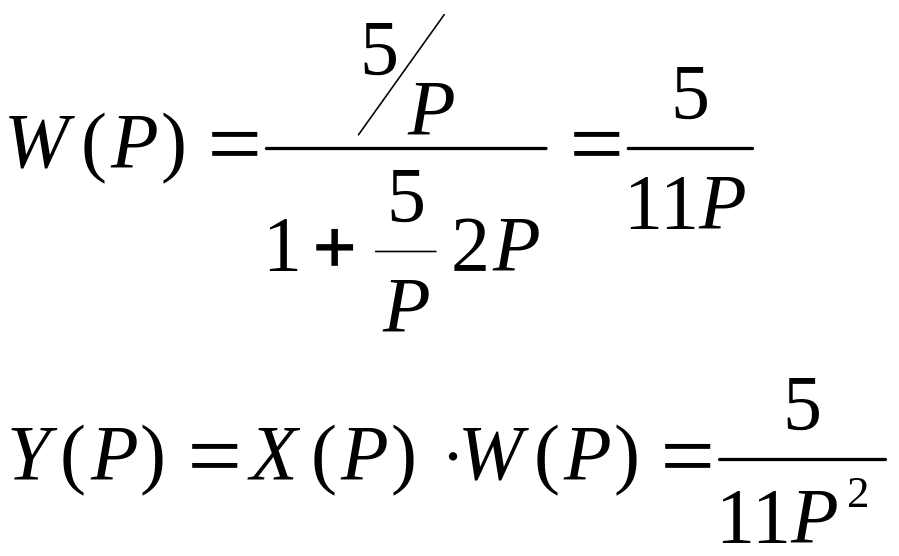
Изображение Лапласа
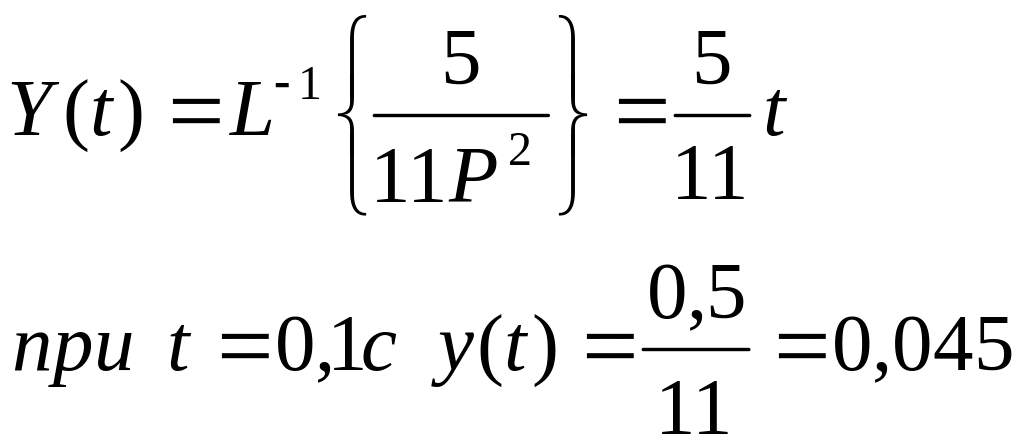
Оригинал
5
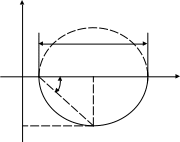
По АФХ определить тип звена и его параметры, если W1=1c-1
V
ω<0
K=1
ω=∞
0 0,5 1 U
450 ω=0
ω>0
-0,5 ω1=1/T
Амплитудно-фазовая характеристика апериодического звена 1го порядка
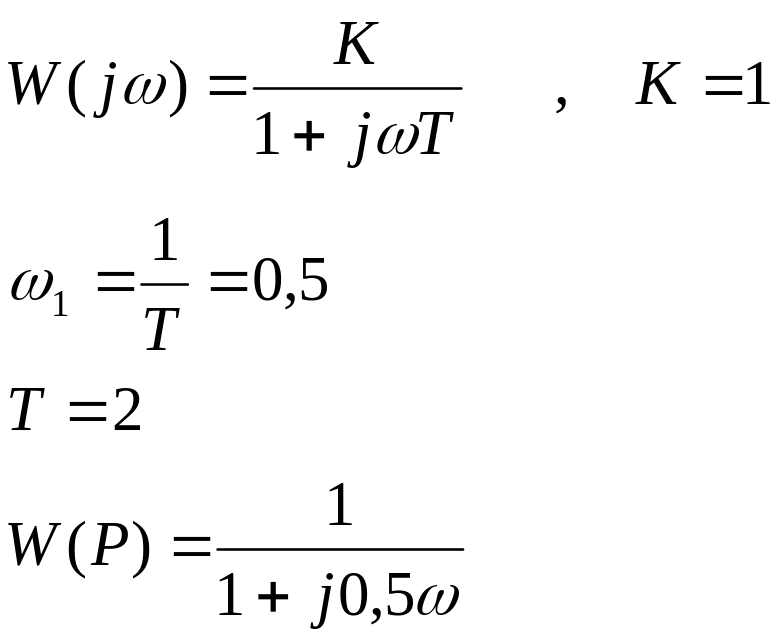
6
Определите статическую ошибку в системе, если Кр=0,1; Ко=3; То=2 сек; Z(t)=0,3·1(t). Полученный результат подтвердите моделированием. Передаточная функция объекта регулирования.
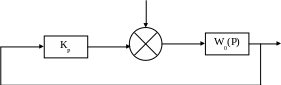
Z(t)
Y(t)
Изображение по Лапласу
Передаточная функция замкнутой системы
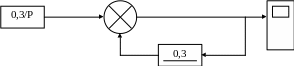
Z(t)
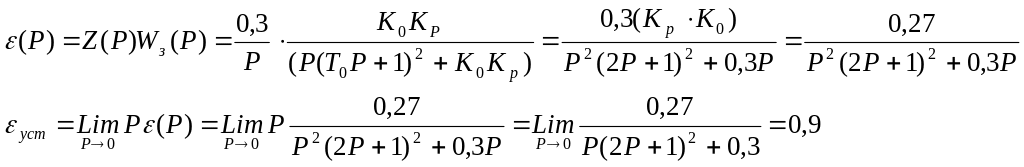
7
Передаточная функция звена
Укажите тип звена:
1 - колебательное
2 – апериодическое II го порядка
3 – консервативное
Т1=1 Т2=0,4
Если звено колебательное, то 0<ξ<1 или Т1\Т2>4 , но Т0\4<4 => звено апериодическое второго порядка Т1≥2Т2
Проверка: 1≥0,8
8
Х
арактеристическое
уравнение замкнутой системы
Определите предельное значение коэффициента усиления из условия устойчивости.
-
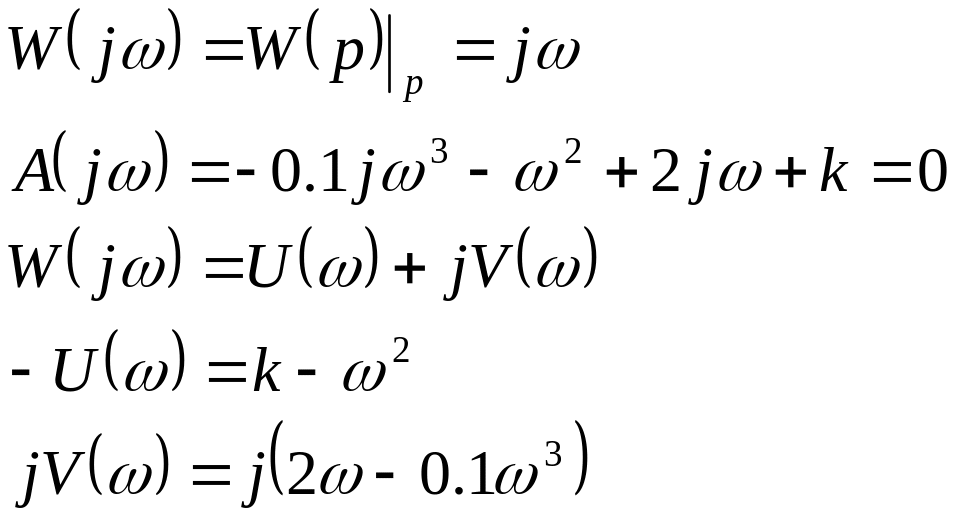
w
U(w)
V(w)
0
10
100
+ ∞
k
k-100
k-10000
- ∞
0
- 80
- 99800
- ∞
V(ω)
ω=0
0 k U(ω)
ω=∞
Исходя из критерия Михайлова при к>0 -система устойчива
к=0 –предельное значение
к<0 –система неустойчива