Ортогональні підпростори та ортогональні доповнення

Нехай U – підпростір евклідового (унітарного) простору V. Ортогональними доповненнями простору U називають множину тих векторів x V, для яких (х, u) = 0 для кожного вектора u U.

Легко переконатися в тому, що для довільної підмножини А V множина

є підпросторами простору і для кожного .

Зокрема, - піпростір простору V.

Два простори та називають ортогональними, якщо

Для довільних векторів та .

Зрозуміло, що U i - ортогональні підпростори.

Теорема 3.2.2. Евклідовий (унітарний) простір V розкладається у пряму суму довільного свого підпростору U та його ортогонального доповнення .

Приклад 6. Застосовуючи процес ортогоналізації, побудувати ортогональну базу лінійної оболонки векторів , , , .

Розв’язання. Як відомо, процес ортогоналізації застосований лише до лінійно незалежних систем векторів. Тому починати процес слід з перевірки даної системи на лінійну залежність. Складаємо матрицю з координат даних векторів і знаходимо її ранг

.

Отже, і вектори утворюють лінійно незалежну систему.

За перший вектор візьмемо :

Вектор шукатимемо у вигляді

Підбираємо так, щоб були ортогональними:

,

Звідси

Але , , значить, , і

Вектор , очевидно також ортогональний до вектора , але має цілі координати. Тому як зручніше брати не , а

Отже, = .

Далі записуємо

і підбираємо так, щоб був ортогональним до і

.

Але , , , ,

Вектор , очевидно, також ортогональний до векторів , . Тому візьмемо

Отже ми одержали ортогональну базу даної лінійної оболонки :

=

.

Ортогональним доповненням підпростору L₁ простору L називається множина всіх векторів простору L , які ортогональні до кожного вектора з L₁.

Приклад. 7 Базисом простору L трьох вимірного евклідового простору V є система векторів =(1,1,2), =(1,1,1).Знайти ортогональну проекцыю і ортогональну складову вектора =(1,2,1) на підпросторі L.Координати векторів дані в ортонормованому базисі простору V.

Розв'язок. Перш за все зноходим скалярний добутку ( , )=5;( , )=4;( , )=6;( , )=4;( , )=3.

Звідси отримуємо наступну систему лінійних рівнянь:

6ξ₁+4ξ₂=5;

4ξ₁+3ξ₂=4.

Розвязоючи її знаходим, що ξ₁=-1/2;ξ₂=2,звідки

=-1/2 +2 =(3/2,3/2,1); = - =(-1/2,1/2,0).

Деякі задачі пов’язані з поняттям ортогональної складової і ортогональної проекції х евклідового простору V на даний простір L.

Вектор з L називається ортогональною проекцією x на L = - ортогональної складової , або ортогональний до всіх векторів простору L топто ортогональний до L. Покажем, як знаходити і .

Нехай ,…, деякий базис простору L.

Тоді, очевидно, що кожний вектор, ортогональний L , буде ортогональнй до кожного вектора базису _,…, . Таким чином отримаємо ,що ( , )=0, або ( - , )=0, або, нарешті,( , )=( , ),i=1,…,m. Після опису вектора в вигляді ₌ξ₁ +…+ξ_{m ,}систему рівнянь( ; )=( , ) можна записати в розгорнутому виді ( , )ξ₁+…+(λ_m, )ξ_m=( , ), i=1,…,m.

Вийшла система з m лінійних рівнянь з m невідомими. Так як визначник матриці відмінний від нуля , то система рівнянь сумісна і має єдиний розв’язок. Якщо a₁,…,a_m ортонормований базис простору L ,то ξ_i=( , ).

Покажем ще , що довжина ортогональної проекції = - вектора на підпросторі L є найменша з відстаней між і будьяким вектором з L. Насправді,так як ортогонально L,то за теоремою

Піфагора, ρ²( , )=ρ² ( , )+ρ²( , )>=ρ²( , ),звідки випливає,що ρ( ,)>=ρ( , ).

Відстань ρ( , ) називається зазвичай відстанню між вектором і підпростором L. Приклад 5. Використовуючи процес ортогоналізації ,перетворити базис простору L

=(1,-1,0,0); = (0,1,-1,0);

=(0,0,1,-1); =(1,0,0,1)

в ортонормований базис.

Розв’язування. Покажем перш за все, що функція (x,y), визначається за формулою (1), насправді виявляється скалярним добутком векторів даного простору. Ясно,що матриця А = з коефіцієнтів виразу (1) є симетричним. Далі можна впевнитись, що квадратна форма (x,x) = ζ²₁ – 2 ζ₁ ζ₂ +2 ζ²₂ -2 ζ₂ ζ₃+2 ζ²₃-2 ζ₃ ζ₄+2 ζ²₄= (ζ₁- ζ₂)²+(ζ₂- ζ₃)²+(ζ₃- ζ₄)²+ ζ²₄. Таким чином, (x,x)>=0 при будь-яких дійсних значеннях ζ₁, ζ₂, ζ₃, ζ₄, при чому (х,х)=0 тільки тоді, коли ζ₁- ζ₂=0; ζ₂- ζ₃=0; ζ₃-ζ₄=0; ζ₄=0, тобто, коли ζ₄= ζ₃= ζ₂=ζ₁=0. Ми бачим, що квадратна форма (х,х) є додатньо визначеною. Тепер підійдемо до процесу ортогоналізації. Припустимо, = ; = +λ , де λ довільне число. Підбираємо λ так, щоб і стали ортогональними:

( , )=( , +λe₁)=( , )+λ( , ), звідки λ=-( , )/( , ).Але

( , )=5;( , )=-4,відповідно λ=4/5 і = +4/5 =

=(4/5,1/5,-1,0).Вектор 5 =(4,1,-1,0) відповідно також ортогональний до вектора ,але має чілі координати.Тому в якості добре брати не (4/5,1/5,-1,0),а (4,1,-1,0).Тобто припустим (4,1,-5,0).

Далі припустимо = +λ₂ +λ₁ і підбираєм λ₁,λ₂ так щоб u₃ став ортогональним до і : ( , )=( +λ₂ +λ₁ )=( , )+λ₂( , )+λ₁( , )=( , )+ +λ₁( , )=0;

λ₁= ( , )/( , );

( , )=( , +λ₂ +λ₁ )=( , )+ +λ₂( , )+λ₁( , )= ( , )+λ₂( , )=0; λ₂=( _, )/ ( , ) .

Так як, згідно з формулою (1),

( , )=5; ( , )=1;( , )=70; ( , )=-16,

Λ₁= - ; λ₂= i = - + =( , ,- ,-1).

Вектор 7 =(5,3,-1,-7) , очевидно , також ортогональний до векторів , .Тому припустимо =(5,3,-1,-7).

На кінець, підбираєм числа μ₁, μ₂, μ₃ так , щоб вектор = +

+μ₃ + μ₂ +μ₁ став ортогональним до векторів , , .

Опустивши деякі очевидні деталі ,отримаємо

( , )=( , )+μ₁( , )=0;

( , )=( , )+μ₂( , )=0;

( , )=( , )+μ₃( , )=0.

Звідки μ₁=- ; μ₂=- ;μ₃= і =( , , , ).

Замість цього вектора можна вз’яти вектор 15 =(10,9,7,4),також ортогональний до , , .Тому отримаємо =(10,9,7,4).І так ми отримали ортогональний базис простору : =(1,-1,0,0); =(4,1,-5,0); =(5,3,-1,-7); =

=(10,9,7,4).Нормуєм вектори , , , , в результаті чого прийдемо до ортонормованого базису:

V₁= / = =( ,- ,0,0);

V₂= / = =

V₃= /

V₄= /

Завдання 1. Дослідити на лінійну залежність систему векторів:

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

2.11.

2.12.

2.13.

2.14.

2.15.

2.16.

2.17.

2.18.

2.19.

2.20.

2.21.

2.22.

2.23.

2.24.

2.25.

2.26.

2.27.

2.28.

2.29.

2.30.

2.31.

Задача 3. Знайти який-небудь базис і визначити розмірність лінійного простору розв’язків системи.

Задача 4. Знайти координати вектора х у базисі , якщо він заданий у базисі .

4.1.

4.2.

4.3.

4.4.

4.5.

4.6.

4.7.

4.8.

4.9.

4.10.

4.11.

4.12.

4.13.

4.14.

4.15.

4.16.

4.17.

4.18.

4.19.

4.20.

4.21.

4.22.

4.23.

4.24.

4.25.

4.26.

4.27.

4.28.

4.29.

4.30.

4.31.

1. Довести, що симетричні матриці утворюють лінійний підпростір простору . (Нагадаємо, що матрицю називають симетричною, якщо ). Знайти базу і розмірність цього підпростору.

2. Довести, що кососиметричні матриці утворюють лінійний підпростір простору . (Нагадаємо, що матрицю називають кососиметричною, якщо ). Знайти базу і розмірність цього підпростору.

3. Довести, що сукупність матриць 2-го порядку , що задовольняють умові , утворюють лінійний підпростір простору . Знайти базу і розмірність цього підпростору.

4. Довести, що сукупність матриць 3-го порядку утворює лінійний підпростір простору . Знайти базу і розмірність цього підпростору.

5. Довести, що сукупність многочленів , що задовольняють умові , утворює лінійний підпростір простору . Знайти базу і розмірність цього підпростору.

6. Довести, що сукупність многочленів , що задовольняють умові , утворює лінійний підпростір . Знайти базу і розмірність цього підпростору.

7. Довести, що сукупність многочленів , що задовольняють умові , утворює лінійний підпростір простору .Знайти базу і розмірність цього підпростору.

8. Довести, що всі -вимірні вектори, координати яких задовольняють умові , утворюють лінійний підпростір простору . Знайти базу і розмірність цього підпростору.

9. Довести, що розв’язки довільної системи однорідних лінійних рівнянь з невідомими рангу утворюють лінійний підпростір простору . Знайти базу і розмірність цього підпростору.

10. Довести, що сукупність матриць 3-го порядку вигляду утворює лінійний підпростір простору . Знайти базу і розмірність цього підпростору.

11. Довести, що скалярний добуток двох довільних векторів і евклідового простору тоді і тільки тоді виражається рівність , коли базис, в якому взяті координати, є ортонормованими.

12. Довести, що координати вектора в ортонормованому базисі обчислюють за формулами , .

13. Довести, якщо в евклідовому просторі справедлива рівність для довільного вектора , то .

14. Довести Піфагора і обернену їй теорему: два вектори і евклідового простору ортогональні тоді і тільки тоді, коли .

15. Довести, що в паралелограмі, натягнутому на вектори і , сума квадратів діагоналей дорівнює сумі квадратів довжин сторін.

16. Довести, що квадрат довжини діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів його ребер, які виходять з однієї вершини.

17. Довести, що тоді і тільки тоді, коли вектори і 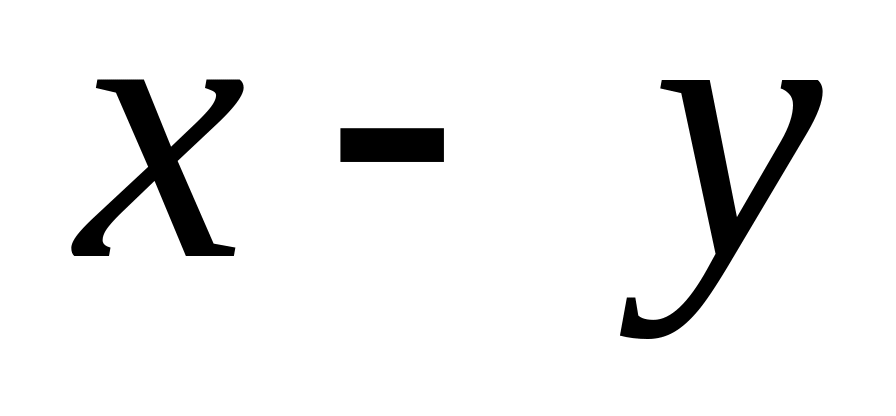ортогональні. Вияснити геометричний зміст цього твердження.

18. Довести, вектори і ортогональні тоді і тільки тоді, коли . Вияснити геометричний зміст цього твердження.

19. Нехай в евклідовому просторі . Знайти і вказати геометричний зміст.

20. Нехай - лінійно залежна система векторів евклідового простору. Вектор ортогональний до всіх . Довести, що система лінійно незалежна.

16