
- •Пример.
- •Определение случайного события.
- •Несовместные события.
- •Вероятность случайного события.
- •Свойства вероятности
- •Классическое определение вероятности события
- •Пример.
- •Основные формулы теории вероятностей Независимость случайных событий.
- •Правило умножения вероятностей
- •Вероятность суммы событий.
- •Некоторые формулы комбинаторики. Правило сложения.
- •Правило умножения.
- •Пример.
- •Размещения и перестановки
- •Сочетания
- •Формула Пуассона
- •Формула полной вероятности.
- •Случайная величина.
- •Пример.
- •Дискретные случайные величины.
- •Непрерывные случайные величины.
- •Числовые характеристики случайных величин.
- •Свойства дисперсии.
- •Некоторые законы распределения. Биномиальный закон распределения.
- •Закон распределения Пуассона.
- •Полиномиальное распределение
- •Пример.
- •Равномерный закон распределения случайной величины.
- •Нормальный закон распределения случайной величины (закон Гаусса).
- •Стандартная форма нормального закона распределения.
- •Распределение «хи-квадрат».
- •График распределения.
- •Показательный (экспоненциальный) закон распределения.
- •Структурные характеристики распределения случайной величины.
- •Медиана.
- •Квантиль.
- •Системы случайных величин.
- •Свойства функции распределения.
- •Свойства плотности вероятности.
- •Математическое ожидание и дисперсия системы случайных величин.
- •Дисперсия двумерной случайной величины.
- •Условное математическое ожидание.
- •Свойства коэффициента корреляции.
- •Функции случайных величин. Функции одной случайной величины.
- •Функция двух случайных величин.
- •Случайные функции.
- •Свойства математического ожидания случайной функции.
- •Свойства дисперсии случайной функции.
- •Свойства корреляционной функции.
- •Свойства взаимной корреляционной функции.
- •Свойства корреляционной функции стационарной случайной функции.
- •Математическая статистика. Выборочный метод.
- •Свойства эмпирической функции распределения.
- •Статистические оценки параметров распределения. Точечные оценки.
- •Метод моментов.
- •Метод наибольшего правдоподобия.
- •Распределение дискретной случайной величины.
- •Распределение непрерывной случайной величины.
- •Распределение выборочных характеристик.
- •Пример 1.
- •Пример 2.
- •3.Распределение выборочной дисперсии.
- •Доверительные интервалы.
- •Проверка статистических гипотез.
- •1.Понятие статистической гипотезы.
- •Проверкa гипотезы о равенствt средних двух нормальных распределений с известными дисперсиями.
- •Двухвыборочный t-тест с одинаковыми и различными дисперсиями.
- •Двухвыборочный f-тест для дисперсий.
- •Парный двухвыборочный t-тест для средних значений.
- •Дисперсионный анализ.
- •Двухфакторный дисперсионный анализ без повторений и с повторениями
Свойства функции распределения.
1.
![]() .
.
2.
![]() -
неубывающая
по каждому
из своих аргументов при фиксированном
значении по другому аргументу:
-
неубывающая
по каждому
из своих аргументов при фиксированном
значении по другому аргументу:
![]()
![]()
![]()
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]()
![]()
![]() ,
,
![]() -
одномерные функции распределения.
-
одномерные функции распределения.
Плотность вероятности (распределения вероятности) двумерной случайной величины - смешанная производная второго порядка от функции распределения.
![]()
Свойства плотности вероятности.
Функция
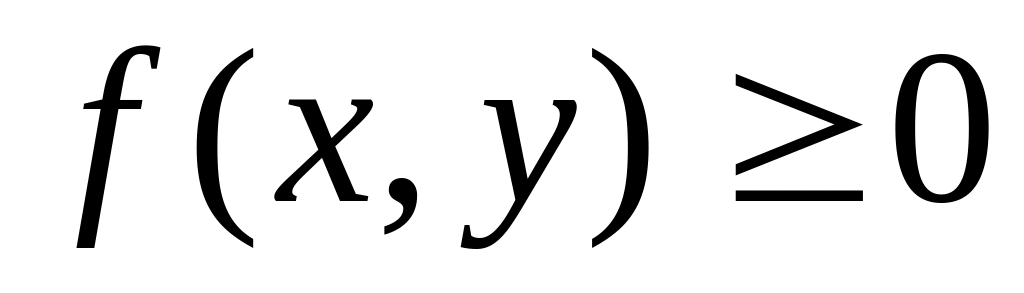 .
. .
.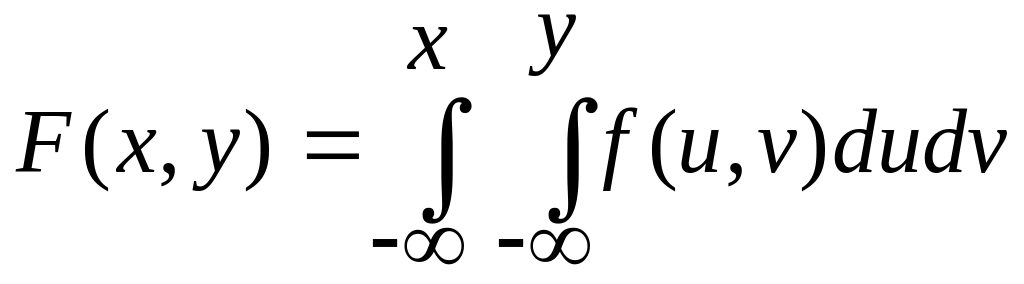 ,
,
где
![]() и
и
![]() - переменные
интегрирования.
- переменные
интегрирования.
4.

Математическое ожидание и дисперсия системы случайных величин.
Математическим ожиданием двумерной случайной величины называется совокупность двух математических ожиданий М[Х], М[Y], то есть упорядоченных пар М[Х], М[Y], которые определяются равенствами:
а) если Х и Y – дискретные случайные величины:
М[Х]=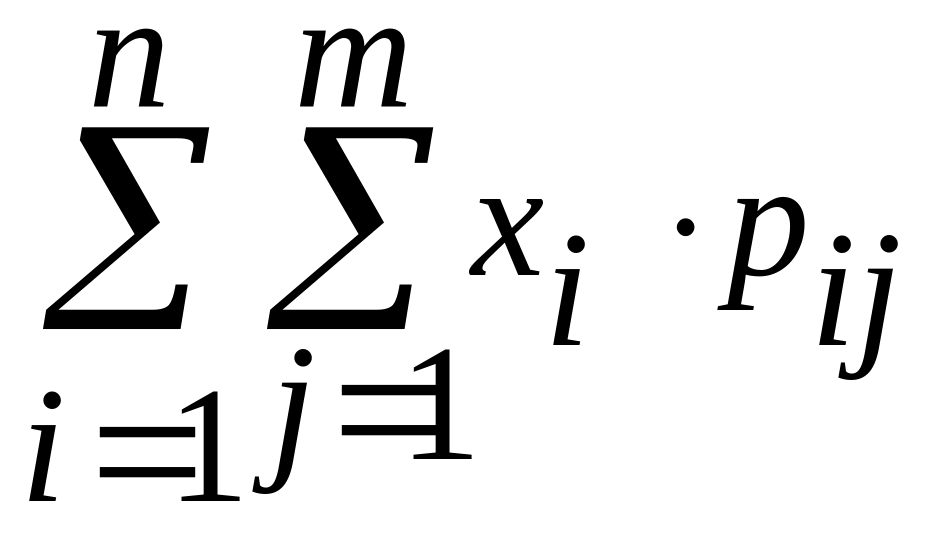 ,
,
![]() :
:
![]() ;
;
![]() .
.
М[Y]=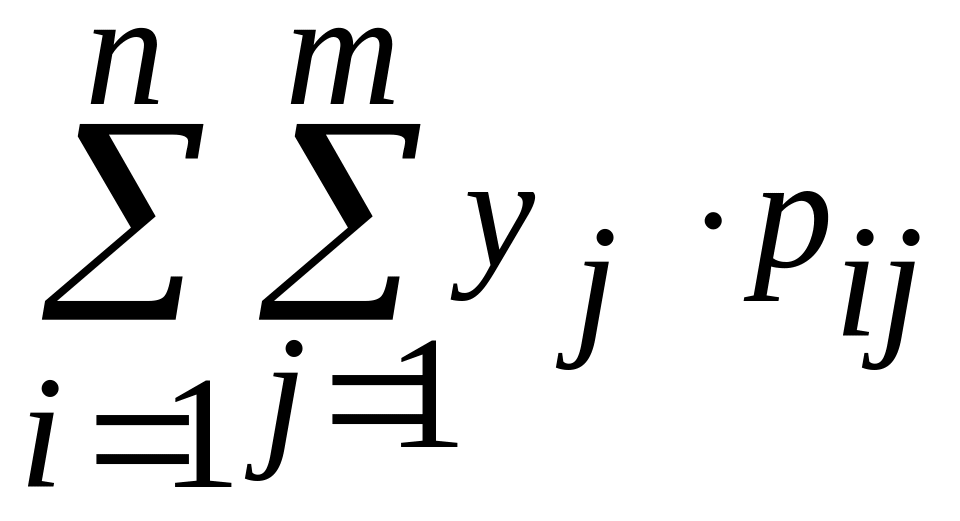 .
.
б) если Х и Y – непрерывные случайные величины:
М[Х]=![]()
М[Y]=![]() ,
,
где
![]() -
плотность вероятности
двумерной случайной величины
.
-
плотность вероятности
двумерной случайной величины
.
Математическое
ожидание
случайной
величины
![]() ,
которая является функцией компонент
,
которая является функцией компонент
![]() двумерной случайной величины
,
находится аналогично по формулам:
двумерной случайной величины
,
находится аналогично по формулам:
М[(Х, Y)]=
 - если Х и
Y
– непрерывные
случайные
величины;
- если Х и
Y
– непрерывные
случайные
величины;М[(Х, Y)]=
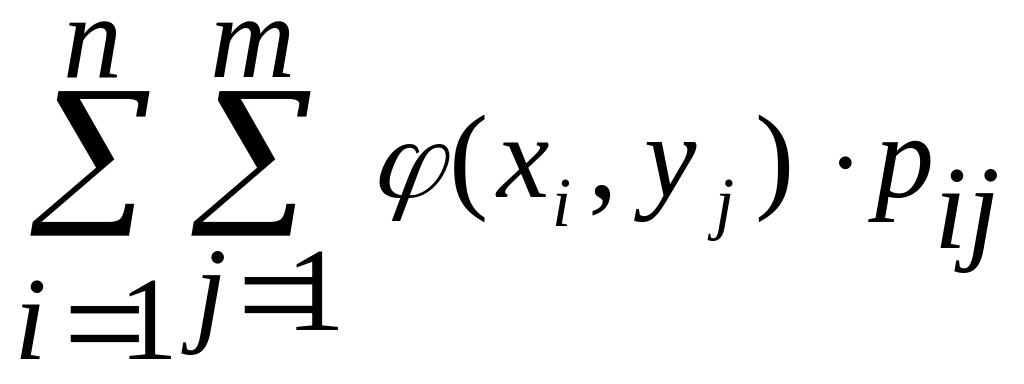 ,
:
;
-
если Х и
Y
– дискретные
случайные
величины.
,
:
;
-
если Х и
Y
– дискретные
случайные
величины.
Дисперсия двумерной случайной величины.
Дисперсия двумерной случайной величины - совокупность двух дисперсий D[X] и D[Y], которые определяются равенствами:
а) если Х и Y – дискретные случайные величины:
D[X]=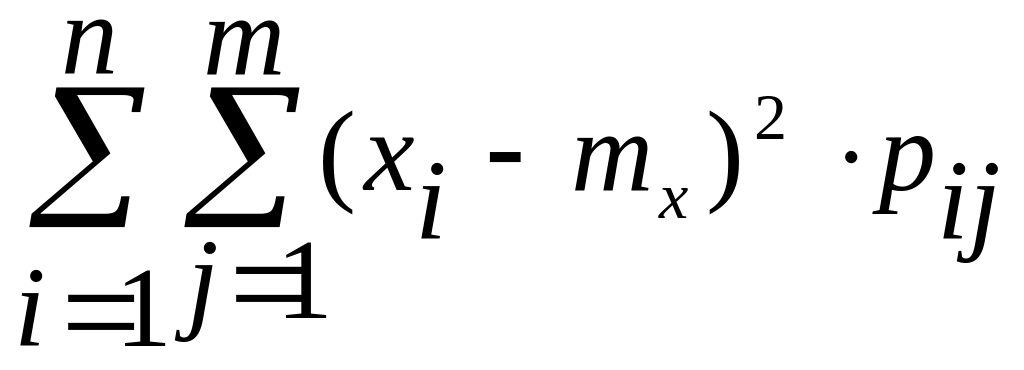 ,
:
;
.
,
:
;
.
D[Y]=
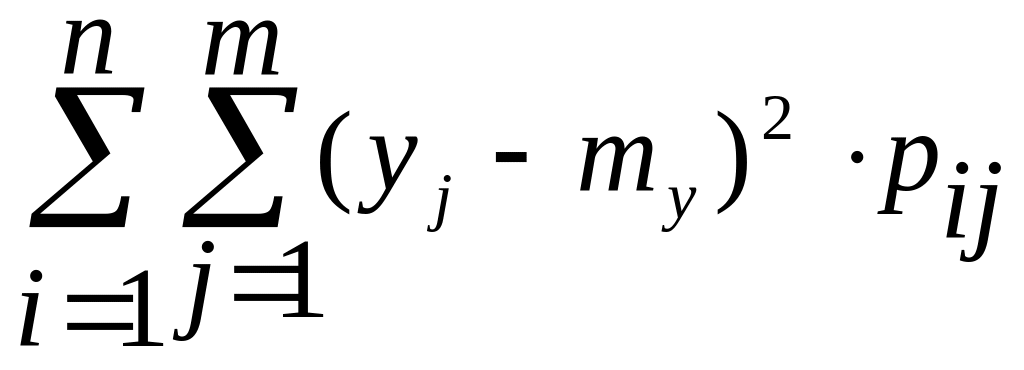 .
.
б) если Х и Y – непрерывные случайные величины:
D[X]=![]()
D[Y]=![]() ,
,
где - плотность вероятности двумерной случайной величины ,
![]() ,
,
![]() -
математические ожидания компонент
.
-
математические ожидания компонент
.
Условное математическое ожидание.
Пусть (X,Y)
– система дискретных случайных величин.
Условным
математическим ожиданием дискретной
случайной
величины Y
при
условии,
что Х=![]() ,
называется величина
,
называется величина
М[Y│X=![]() ]=
]=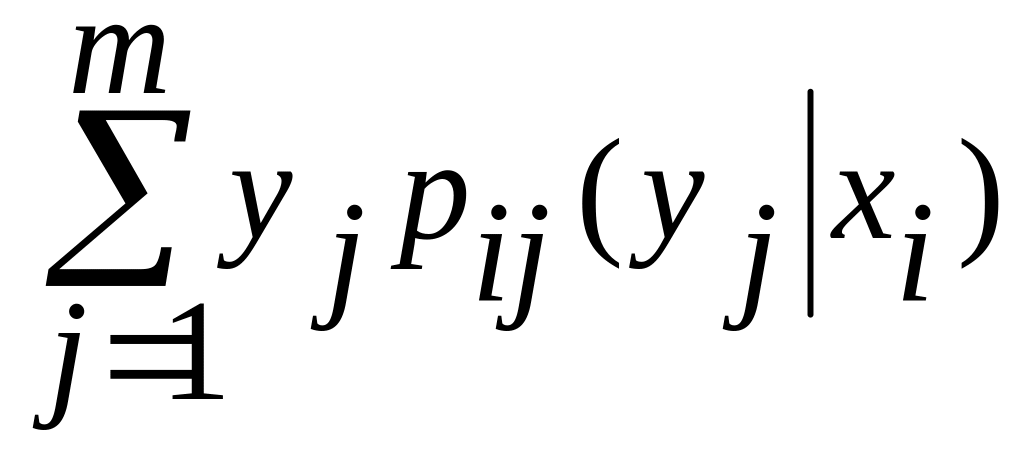 .
.
Аналогично, условным математическим ожиданием дискретной случайной величины X при условии, что Y=yj, называется величина
М[Х│Y=![]() ]=
]=![]() ,
:
;
.
,
:
;
.
Пусть - система непрерывных случайных величин. В этом случае условное математическое ожидание случайной величины Y при условии, что Х=xi, определяется равенством:
М[Y│![]() ]=
]=![]() .
.
Аналогично, условное математическое ожидание случайной величины X при условии, что Y=yj, определяется равенством:
М[Х│![]() ]=
]=![]()
Для характеристики связи между величинами Х и Y служит корреляционный момент:
Kxy=М[ ]=M[(X – mx)M(Y – my)].
Используя понятие корреляционного момента запишем еще одно свойство дисперсии, а именно - дисперсия суммы двух случайных величин определяется равенством:
D[X+Y] = D[X]+D[Y]+2Kxy
Корреляционный момент иначе называется ковариация и обозначается cov(Х, Y).
Величина корреляционного момента вычисляется по формулам:
а) если Х и Y – дискретные случайные величины:
Kxy= ,
:
;
.
,
:
;
.
б) если Х и Y – непрерывные случайные величины:
Kxy=![]() ,
,
где - плотность вероятности двумерной случайной величины ,
, - математические ожидания компонент .
Корреляционный момент удобно вычислять по формуле:
Kxy=М[ХY]-М[Х]М[Y].
Если Х
и Y
независимы,
то
Kxy=0.
Таким образом,
если Kxy
![]() 0,
то
случайные
величины Х
и Y
зависимы.
В этом случае случайные величины Х
и Y
называются коррелированными.
0,
то
случайные
величины Х
и Y
зависимы.
В этом случае случайные величины Х
и Y
называются коррелированными.
Когда Kxy=0, случайные величины Х и Y называются некоррелированными.
Из рассмотренного свойства корреляционного момента получаем важное следствие. Дисперсия суммы двух случайных величин равна сумме их дисперсий если величины X и Y независимы, т.е.
D[X+Y] = D[X]+D[Y]+2Kxy
Коэффициент корреляции (rxy) для двух случайных величин Х и Y есть безразмерная величина:
rxy=![]() ,
,
где
![]() ,
,![]() - средние
квадратические отклонения величин Х
и Y
соответственно.
- средние
квадратические отклонения величин Х
и Y
соответственно.
![]()
![]()
Коэффициент корреляции характеризует степень линейной зависимости двух случайных величин Х и Y.
