График распределения.

При увеличении числа степеней свободы F-распределение Фишера приближается к нормальному распределению.

Показательный (экспоненциальный) закон распределения.

Случайная величина Х распределена по экспоненциальному закону, если она имеет плотность вероятности следующего вида:

0, если

, если .

F(x) при х .

F(x) при х .

М[Х]=

D[X]=

Вероятность попадания случайной величины на интервал (a, b):

Р(a<X b)= .

Этот закон широко используется при определении надёжности элементов сложных систем и систем в целом. (Элемент – устройство.) Пусть элемент начинает работать в момент времени t₀=0 и в момент времени t происходит отказ этого элемента. Промежуток времени Т между t₀ и t называется временем безотказной работы.

Функция распределения времени безотказной работы подчиняется экспоненциальному закону:

, а величина называется функцией надёжности.

Структурные характеристики распределения случайной величины.

К структурным характеристикам относятся такие характеристики, как начальные и центральные моменты. Структурные характеристики определяют некоторые свойства случайных величин.

Начальный момент порядка k случайной величины Х:

Для дискретной случайной величины начальный момент k порядка

, где - вероятность, - значение случайной величины.

Для непрерывной случайной величины, имеющей плотность вероятности , начальный момент k порядка

.

Центральный момент случайной величины Х – величина, которая определяется как .

Особое значение имеют такие показатели начального и центрального моменты, которые называются коэффициент ассиметрии

и коэффициент эксцесса

.

Для нормального распределения справедливо:

0

0.

Мода.

Мода случайной величины Х – это наиболее вероятное значение х.

.

(нахождение экстремума функции )

Медиана.

Медиана случайной величины Х – это значение случайной величины Х - x_p, для которого выполняется условие .

.

Квантиль.

Квантиль уровня q – это такое значение случайной величины Х - x_p, для которого справедливо равенство (вероятность события « » равняется некоторой вероятности ).

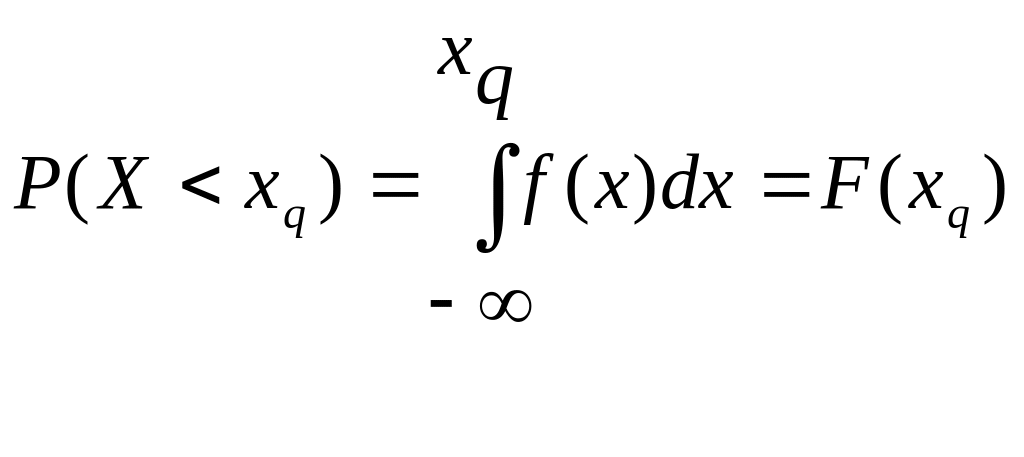
- обратная функция к функции распределения при заданном значении вероятности .

Задавая , можно определить , зная значение случайной величины.

На графике плотности вероятности - это такое значение , при котором площадь под кривой графика плотности вероятности, определённой на интервале равняется .

Системы случайных величин.

Во многих практических задачах результат опыта описывается не одной случайной величиной, а двумя и более случайными величинами. Если он описывается случайными величинами Х и Y, то говорят о системе двух случайных величин, или о двумерной случайной величине.

Если случайных величин больше, то говорят о многомерной (n-мерной) случайной величине.

Геометрически двумерную случайную величину можно представить как точку на плоскости. Для любой n-мерной случайной величины справедливы такие понятия, как закон распределения, функция распределения, плотность вероятности и т.д.

Мы говорим, что задана двумерная случайная величина (X, Y), если каждому множеству (борелевскому) A на координатной плоскости R² сопоставлено неотрицательное число p(A), причем p(R²) = 1. Закон распределения двумерной случайной величины можно записать следующим образом.

Для дискретной двумерной случайной величины (X, Y) закон распределения задается выражением:

, : ; .

где p_ij - вероятность того, что в данном опыте случайная величина Х примет значение x_i, а случайная величина Y - y_j для любых значений i и j.

Также закон распределения дискретной двумерной случайной величины можно задать в виде таблицы вида:

	y1	y2	y3				ym
х1	p11	p12		…			pm1
х2
х3
…
хn	Pn1	Pn2					pnm

По аналогии с одномерной случайной величиной введем понятие функция распределения двумерной случайной величины (X,Y)

т.е. F(x,y) есть вероятность попадания случайной точки в область R_xy где R_xy множество точек абсциссы которых меньше числа x, а ординаты меньше y.

Функция распределения двумерной дискретной случайной величины имеет следующий вид:

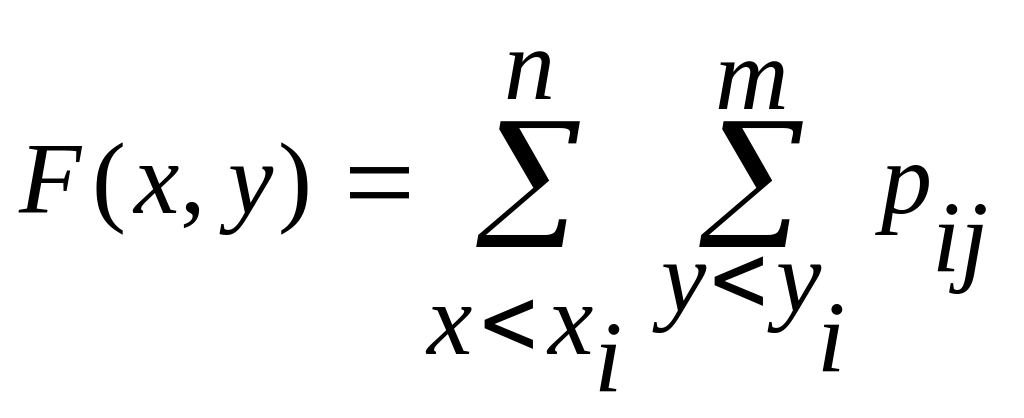
Вероятность попадания двумерной случайной величины в заданный прямоугольник можно определить, используя соотношение: