
- •Пример.
- •Определение случайного события.
- •Несовместные события.
- •Вероятность случайного события.
- •Свойства вероятности
- •Классическое определение вероятности события
- •Пример.
- •Основные формулы теории вероятностей Независимость случайных событий.
- •Правило умножения вероятностей
- •Вероятность суммы событий.
- •Некоторые формулы комбинаторики. Правило сложения.
- •Правило умножения.
- •Пример.
- •Размещения и перестановки
- •Сочетания
- •Формула Пуассона
- •Формула полной вероятности.
- •Случайная величина.
- •Пример.
- •Дискретные случайные величины.
- •Непрерывные случайные величины.
- •Числовые характеристики случайных величин.
- •Свойства дисперсии.
- •Некоторые законы распределения. Биномиальный закон распределения.
- •Закон распределения Пуассона.
- •Полиномиальное распределение
- •Пример.
- •Равномерный закон распределения случайной величины.
- •Нормальный закон распределения случайной величины (закон Гаусса).
- •Стандартная форма нормального закона распределения.
- •Распределение «хи-квадрат».
- •График распределения.
- •Показательный (экспоненциальный) закон распределения.
- •Структурные характеристики распределения случайной величины.
- •Медиана.
- •Квантиль.
- •Системы случайных величин.
- •Свойства функции распределения.
- •Свойства плотности вероятности.
- •Математическое ожидание и дисперсия системы случайных величин.
- •Дисперсия двумерной случайной величины.
- •Условное математическое ожидание.
- •Свойства коэффициента корреляции.
- •Функции случайных величин. Функции одной случайной величины.
- •Функция двух случайных величин.
- •Случайные функции.
- •Свойства математического ожидания случайной функции.
- •Свойства дисперсии случайной функции.
- •Свойства корреляционной функции.
- •Свойства взаимной корреляционной функции.
- •Свойства корреляционной функции стационарной случайной функции.
- •Математическая статистика. Выборочный метод.
- •Свойства эмпирической функции распределения.
- •Статистические оценки параметров распределения. Точечные оценки.
- •Метод моментов.
- •Метод наибольшего правдоподобия.
- •Распределение дискретной случайной величины.
- •Распределение непрерывной случайной величины.
- •Распределение выборочных характеристик.
- •Пример 1.
- •Пример 2.
- •3.Распределение выборочной дисперсии.
- •Доверительные интервалы.
- •Проверка статистических гипотез.
- •1.Понятие статистической гипотезы.
- •Проверкa гипотезы о равенствt средних двух нормальных распределений с известными дисперсиями.
- •Двухвыборочный t-тест с одинаковыми и различными дисперсиями.
- •Двухвыборочный f-тест для дисперсий.
- •Парный двухвыборочный t-тест для средних значений.
- •Дисперсионный анализ.
- •Двухфакторный дисперсионный анализ без повторений и с повторениями
Формула Пуассона
Формула Пуассона
используется при расчёте вероятностей
редких событий, когда
![]() ,
,
![]() .
.
Обозначим через
![]() среднее число успехов.
среднее число успехов.
Вероятность того, что число успехов будет равно m при n испытаниях, можно найти по формуле:
![]() .
.
Пример.
Выпекаются булочки с изюмом. Обозначим: n – число изюминок, N - число булочек.
Найти вероятность того, что в булочке будет ровно k изюминок.
Здесь
,
.
Среднее число изюминок составляет
![]() (средняя
плотность). Тогда
(средняя
плотность). Тогда
![]()
Формула полной вероятности.
Пусть А – случайное событие, которое происходит только совместно с одним из событий Н1, Н2, …, Нn , которые образуют полную группу событий. События Н1, Н2, …, Нn в теории вероятностей называются гипотезами.
Вероятность р(А) можно определить с помощью формулы полной вероятности:
р(А)=р(Н1)×р(А /Н1 )+р(Н2)×р(А /Н2 )+…+р(Нn)×р(А /Нn ).
Пример.
Клиентами некоторого банка являются: государственные организации, коммерческие организации, физические лица. На их долю приходятся следующие объемы заимствованных средств: государственные организации - 5%, коммерческие организации - 15%, физические лица – остальной объем кредита. Определить общую вероятность невозврата кредита, если вероятность невозврата кредита государственной организацией составляет 0,001, коммерческой организацией - 0,01, физическими лицами - 0,1.
Обозначим:
событие А – не возврат кредита, Р(А) – вероятность события А.
Н1 – не возврат кредита государственной организацией
Н2 – не возврат кредита коммерческой организацией
Н3 – не возврат кредита физическими лицами
р(Н1)=5%, р(Н2)=15%, р(Н3)=80%, р(А / Н1 ) =0,001 , р(А / Н2 )=0,01 , р(А / Н3 )=0,1.
По формуле полной вероятности находим:
р(А)=р(Н1)×р(А|Н1 )+ р(Н2)× р(А|Н2 )+ р(Н3)×
×р(А|Н3)=0,05×0,001+0,15×0,01+0,8×0,1=0,082.
Наряду с формулой полной вероятности, используется формула Байеса:
р(Нi|А )=(р(Нi )×р(А|Нi))/р(А),
где р(А) рассчитывается по формуле полной вероятности. Формула Байеса позволяет определить вероятность осуществления гипотезы в случае если произошло событие А.
Случайная величина.
Часто с каждым из возможных исходов опыта можно связать некоторое число.
Пример.
При бросании кубика с исходом опыта можно связать число, нанесённое на грань этого кубика: например Ω={1,2,3,4,5,6}. Число, которое выпадает при бросании кубика есть случайная величина.
Число часов безотказной работы лампочки.
Время ожидания автобуса на остановке.
Случайная
величина Х есть
числовая функция, определённая на
множестве элементарных событий Ω.
Случайная
величина Х
каждому элементарному событию
ставит в
соответствие число Х()=Х,
![]() Ω.
Ω.
Будем обозначать:
Х, Y – случайные величины.
х, y – реализации случайной величины в данном опыте.
Случайные величины делятся на дискретные и непрерывные.
Дискретные случайные величины.
Дискретная случайная величина Х задаётся конечной или счётной последовательностью x 1, x 2,…, x i, … и значениями p1, p 2,…, pi, … вероятностей, с которыми появляются значения x 1, x 2,…, x i, … .
Любая случайная величина полностью описывается законом распределения. Под законом распределения понимают любой способ, с помощью которого можно значениям случайной величины Х: x 1, x 2,… поставить в соответствие вероятности p1, p 2,…
Способы задания случайной величины:
табличный
Х |
x 1 |
x 2 |
… |
x i |
… |
p |
p1 |
p 2 |
… |
pi |
… |
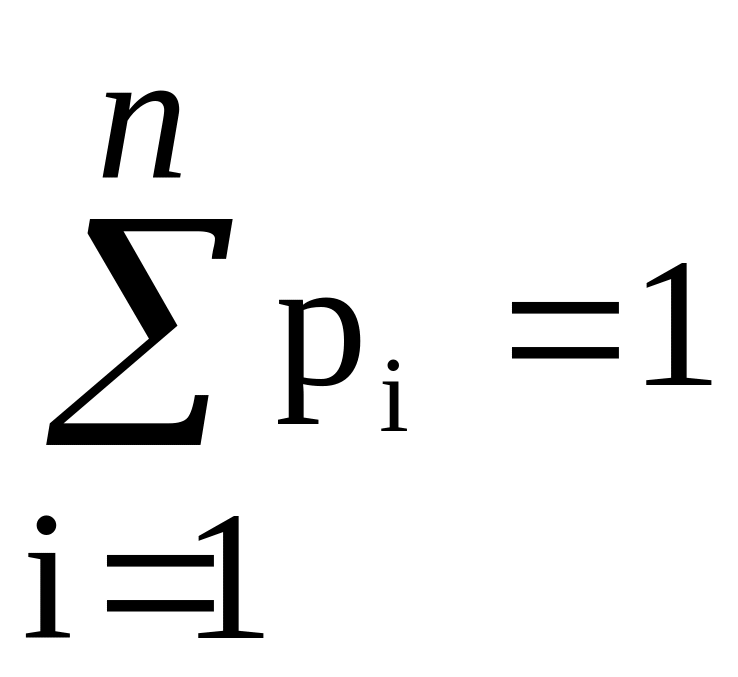
При одном бросании кубика число очков Х:
Х |
1 |
2 |
3 |
4 |
5 |
6 |
p |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
F(x) |
1/6 |
2/6 |
3/6 |
4/6 |
5/6 |
6/6 |
графический
При графическом способе используется функция распределения.
аналитический
Закон распределения дискретной случайной величины можно задать с помощью функции распределения F(x):
F(x)=Р(Х<x)
Для дискретной случайной величины функцию распределения можно задать с помощью
F(x)=![]() .
.
Свойства функции распределения случайной величины:
F(x) – неубывающая функция.
F(x)
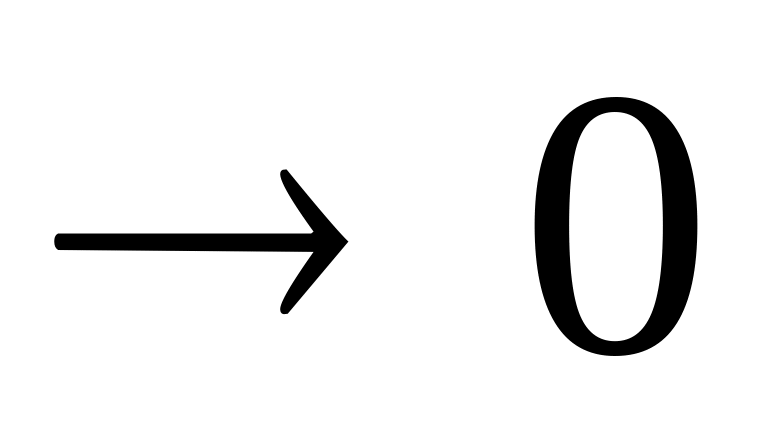 при х
при х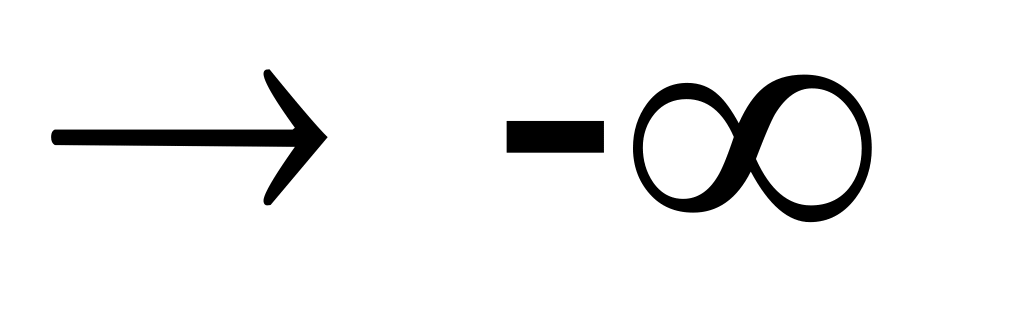 .
.F(x)
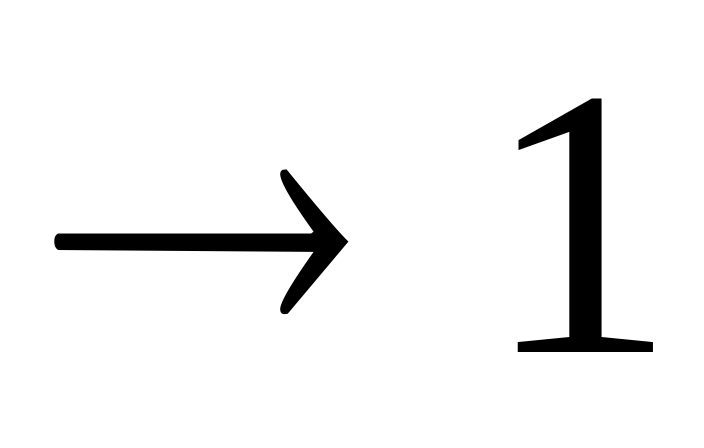 при х
при х .
.F(x) непрерывна слева.
