
- •Пример.
- •Определение случайного события.
- •Несовместные события.
- •Вероятность случайного события.
- •Свойства вероятности
- •Классическое определение вероятности события
- •Пример.
- •Основные формулы теории вероятностей Независимость случайных событий.
- •Правило умножения вероятностей
- •Вероятность суммы событий.
- •Некоторые формулы комбинаторики. Правило сложения.
- •Правило умножения.
- •Пример.
- •Размещения и перестановки
- •Сочетания
- •Формула Пуассона
- •Формула полной вероятности.
- •Случайная величина.
- •Пример.
- •Дискретные случайные величины.
- •Непрерывные случайные величины.
- •Числовые характеристики случайных величин.
- •Свойства дисперсии.
- •Некоторые законы распределения. Биномиальный закон распределения.
- •Закон распределения Пуассона.
- •Полиномиальное распределение
- •Пример.
- •Равномерный закон распределения случайной величины.
- •Нормальный закон распределения случайной величины (закон Гаусса).
- •Стандартная форма нормального закона распределения.
- •Распределение «хи-квадрат».
- •График распределения.
- •Показательный (экспоненциальный) закон распределения.
- •Структурные характеристики распределения случайной величины.
- •Медиана.
- •Квантиль.
- •Системы случайных величин.
- •Свойства функции распределения.
- •Свойства плотности вероятности.
- •Математическое ожидание и дисперсия системы случайных величин.
- •Дисперсия двумерной случайной величины.
- •Условное математическое ожидание.
- •Свойства коэффициента корреляции.
- •Функции случайных величин. Функции одной случайной величины.
- •Функция двух случайных величин.
- •Случайные функции.
- •Свойства математического ожидания случайной функции.
- •Свойства дисперсии случайной функции.
- •Свойства корреляционной функции.
- •Свойства взаимной корреляционной функции.
- •Свойства корреляционной функции стационарной случайной функции.
- •Математическая статистика. Выборочный метод.
- •Свойства эмпирической функции распределения.
- •Статистические оценки параметров распределения. Точечные оценки.
- •Метод моментов.
- •Метод наибольшего правдоподобия.
- •Распределение дискретной случайной величины.
- •Распределение непрерывной случайной величины.
- •Распределение выборочных характеристик.
- •Пример 1.
- •Пример 2.
- •3.Распределение выборочной дисперсии.
- •Доверительные интервалы.
- •Проверка статистических гипотез.
- •1.Понятие статистической гипотезы.
- •Проверкa гипотезы о равенствt средних двух нормальных распределений с известными дисперсиями.
- •Двухвыборочный t-тест с одинаковыми и различными дисперсиями.
- •Двухвыборочный f-тест для дисперсий.
- •Парный двухвыборочный t-тест для средних значений.
- •Дисперсионный анализ.
- •Двухфакторный дисперсионный анализ без повторений и с повторениями
Двухфакторный дисперсионный анализ без повторений и с повторениями
Аналогично задаче однофакторного дисперсионного анализа можно рассмотреть задачу о действии на результативный признак Y двух факторов – A и B.
Логика однофакторного и двухфакторного дисперсионного анализа во многом схожа и состоит в следующем.
Пусть
![]() -
математическое ожидание результативного
признака
Y
при уровне
A(j)
(j
= 1,
2, … ca)
;
-
математическое ожидание результативного
признака
Y
при уровне
A(j)
(j
= 1,
2, … ca)
;
![]() -
математическое ожидание результативного
признака Y
при уровне B(l)
(l
= 1, 2, … cb).
Если
при изменении уровня фактора A
групповые
математические ожидания
не изменяются, то
считаем,
что результативный
признак не зависит от фактора А,
в
противном случае
такая зависимость имеется. Аналогично,
если при изменении уровня фактора B
сохраняется равенство групповых
математических ожиданий,
то
считаем,
что Y
не зависит от фактора B.
Но
поскольку числовые значения математических
ожиданий неизвестны, возникает задача
проверки следующих гипотез:
-
математическое ожидание результативного
признака Y
при уровне B(l)
(l
= 1, 2, … cb).
Если
при изменении уровня фактора A
групповые
математические ожидания
не изменяются, то
считаем,
что результативный
признак не зависит от фактора А,
в
противном случае
такая зависимость имеется. Аналогично,
если при изменении уровня фактора B
сохраняется равенство групповых
математических ожиданий,
то
считаем,
что Y
не зависит от фактора B.
Но
поскольку числовые значения математических
ожиданий неизвестны, возникает задача
проверки следующих гипотез:
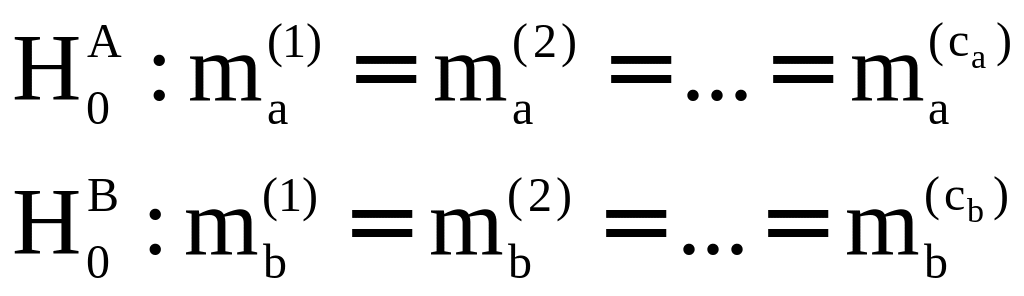
Проверять эти гипотезы, так же как и в задаче однофакторного дисперсионного анализа, можно только при соблюдении следующих требований:
1) при различных сочетаниях уровней факторов A и B наблюдения независимы;
2) при каждом сочетании уровней факторов A и B результативный признак Y имеет нормальный закон распределения с постоянной для различных сочетаний генеральной дисперсией σ2.
Основой проведения
двухфакторного дисперсионного анализа
служит комбинационная группировка по
двум факторам с последующим разложением
полной вариации результативного признака
![]() на сумму вариаций фактора A
и фактора B,
вариации взаимодействия и случайной
ошибки по формуле
на сумму вариаций фактора A
и фактора B,
вариации взаимодействия и случайной
ошибки по формуле
![]()
где:
![]() - полная вариация.
Определяется как полная сумма квадратов
отклонения от общего среднего:
- полная вариация.
Определяется как полная сумма квадратов
отклонения от общего среднего:
![]() .
.
Общее среднее значение равно:
![]()
![]() - вариация фактора
A
—
показатель вариации,
вызванной влиянием на Y
фактора
A;
- вариация фактора
A
—
показатель вариации,
вызванной влиянием на Y
фактора
A;
![]()
где
![]() -
среднее значение, соответствующее j
– ому уровню фактора A
-
среднее значение, соответствующее j
– ому уровню фактора A
![]()
![]() - вариация фактора
В —
показатель вариации,
вызванной влиянием на Y
фактора B;
- вариация фактора
В —
показатель вариации,
вызванной влиянием на Y
фактора B;
![]()
где
![]() -
среднее значение, соответствующее l
– ому уровню фактора B
-
среднее значение, соответствующее l
– ому уровню фактора B
![]()
![]() -
вариация
взаимодействия. Определяет эффект
взаимодействия между факторами A
и B.
-
вариация
взаимодействия. Определяет эффект
взаимодействия между факторами A
и B.
![]()
где
![]() -
среднее значение, соответствующее i
–ому уровню фактора A
и l
– ому уровню фактора B
-
среднее значение, соответствующее i
–ому уровню фактора A
и l
– ому уровню фактора B
![]()
![]() - случайная ошибка.
Показатель
вариации,
вызванной влиянием на Y
остаточных
факторов.
- случайная ошибка.
Показатель
вариации,
вызванной влиянием на Y
остаточных
факторов.
Если каждую сумму
квадратов отклонений разделить на
соответствующее число степеней свободы,
то получится четыре типа дисперсии
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
В двухфакторном дисперсионном анализе применяются три разных критерия.
Для
проверки гипотезы об отсутствии эффекта
фактора A
![]() и альтернативной гипотезы H1:
не все mj
равны используется F
– критерий Фишера:
и альтернативной гипотезы H1:
не все mj
равны используется F
– критерий Фишера:
![]() ,
,
В
математической статистике доказывается,
что если гипотеза
![]() верна,
то величина
верна,
то величина
![]() имеет
F
- распределение с числом степеней свободы
df1
= (ka
– 1) и df2
= (ka
– 1)
(kb
– 1).
имеет
F
- распределение с числом степеней свободы
df1
= (ka
– 1) и df2
= (ka
– 1)
(kb
– 1).
Для
проверки гипотезы об отсутствии эффекта
фактора B
![]() и альтернативной гипотезы H1:
не все ml
равны используется F
– критерий Фишера:
и альтернативной гипотезы H1:
не все ml
равны используется F
– критерий Фишера:
![]() ,
,
В
математической статистике доказывается,
что если гипотеза
![]() верна,
то величина
верна,
то величина
![]() имеет
F
- распределение с числом степеней свободы
df1
= (cb
– 1) и df2
= (ca
– 1)
(cb
– 1).
имеет
F
- распределение с числом степеней свободы
df1
= (cb
– 1) и df2
= (ca
– 1)
(cb
– 1).
Для проверки гипотезы об отсутствии эффекта взаимодействия факторов A и B
![]() :
взаимодействие факторов A
и B
равно нулю
:
взаимодействие факторов A
и B
равно нулю
и альтернативной гипотезы
![]() H1:
взаимодействие факторов A
и B
не равно нулю
H1:
взаимодействие факторов A
и B
не равно нулю
используется F – критерий Фишера:
![]() ,
,
Проверка
выдвинутых гипотез осуществляется так
же, как и при
однофакторном дисперсионном анализе,
и состоит в нахождении
правосторонних критических интервалов
![]() с
последующим
контролем попадания (или непопадания)
в данный интервал
расчетных значений FA
(или
FB)
Если
расчетное значение попадает
в критический интервал, то гипотеза
(
с
последующим
контролем попадания (или непопадания)
в данный интервал
расчетных значений FA
(или
FB)
Если
расчетное значение попадает
в критический интервал, то гипотеза
(![]() )
отвергается,
т.е. считается,
что фактор A
(B)
влияет
на результативный признак Y
)
отвергается,
т.е. считается,
что фактор A
(B)
влияет
на результативный признак Y
Двухфакторный дисперсионный анализ может иметь две разновидности:: без повторений и с повторениями. В первом случае каждому уровню факторов соответствует только одна выборка данных, во втором — определенным уровням факторов может соответствовать более одной выборки данных.
Пример двухфакторного дисперсионного анализа с повторениями.
Исследуется зависимость продолжительности работы подшипников при автоколебании нагревании. Данные эксперимента приведены в таблице
|
Слабое нагревание |
Сильное нагревание |
Слабое автоколебание |
12 |
26 |
|
24 |
16 |
Сильное автоколебание |
18 |
101 |
|
28 |
113 |
Инструмент анализа Excel «Двухфакторный дисперсионный анализ с повторениями» служит для выяснения на основе выборочных данных факта влияния контролируемых факторов A и B на результативный признак Y. В диалоговом окне задаются те же параметры, что и в диалоговом окне «Однофакторный дисперсионный анализ», только добавлено поле Число строк для выборки. B это поле вводится число наблюдений, приходящихся на каждый уровень одного из факторов. Каждый уровень фактора должен содержать одно и то же количество наблюдений (строк таблицы).
Результаты расчетов приведены в таблице
Двухфакторный дисперсионный анализ с повторениями |
|
|||||
|
|
|
|
|
|
|
ИТОГИ |
Слабое нагревание |
Сильное нагревание |
Итого |
|
|
|
Слабое автоколебание |
|
|
|
|
|
|
Счет |
2 |
2 |
4 |
|
|
|
Сумма |
36 |
42 |
78 |
|
|
|
Среднее |
18 |
21 |
19,5 |
|
|
|
Дисперсия |
72 |
50 |
43,66667 |
|
|
|
|
|
|
|
|
|
|
Сильное автоколебание |
|
|
|
|
|
|
Счет |
2 |
2 |
4 |
|
|
|
Сумма |
46 |
214 |
260 |
|
|
|
Среднее |
23 |
107 |
65 |
|
|
|
Дисперсия |
50 |
72 |
2392,667 |
|
|
|
|
|
|
|
|
|
|
Итого |
|
|
|
|
|
|
Счет |
4 |
4 |
|
|
|
|
Сумма |
82 |
256 |
|
|
|
|
Среднее |
20,5 |
64 |
|
|
|
|
Дисперсия |
49 |
2506 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
|
||
Источник вариации |
SS |
df |
MS |
F |
P-Значение |
F критическое |
Выборка |
4140,5 |
1 |
4140,5 |
67,87705 |
0,001184 |
7,70865 |
Столбцы |
3784,5 |
1 |
3784,5 |
62,04098 |
0,001404 |
7,70865 |
Взаимодействие |
3280,5 |
1 |
3280,5 |
53,77869 |
0,00184 |
7,70865 |
Внутри |
244 |
4 |
61 |
|
|
|
|
|
|
|
|
|
|
Итого |
11449,5 |
7 |
|
|
|
|
Анализ полученных результатов позволяет сделать следующие выводы.
Гипотезу об отсутствие статистически значимого эффекта взаимодействия ( ) следует отклонить поскольку
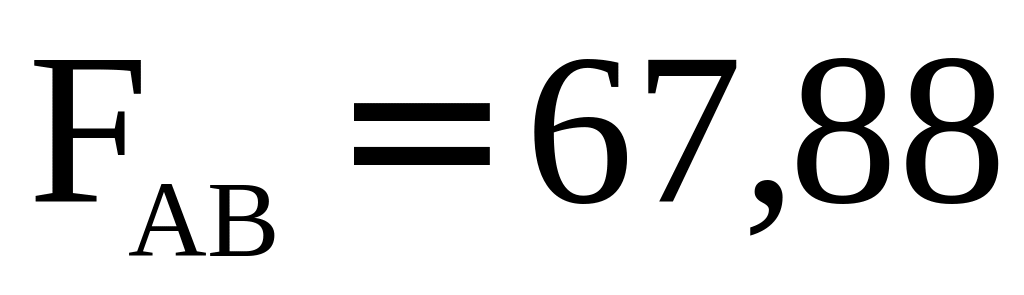 больше критического значения 7,7
(соответственно p
– значение меньше уровня значимости
α = 0,05) ;
больше критического значения 7,7
(соответственно p
– значение меньше уровня значимости
α = 0,05) ;Гипотезу об отсутствие статистически значимого эффекта взаимодействия ( ) следует отклонить поскольку больше критического значения 7,7 (соответственно p – значение меньше уровня значимости α = 0,05) ;
Гипотезу об отсутствие статистически значимого эффекта взаимодействия ( ) следует отклонить поскольку больше критического значения 7,7 (соответственно p – значение меньше уровня значимости α = 0,05) ;
Двухфакторный дисперсионный анализ с повторениями
Дисперсионный анализ |
|
|
|
|
||
Источник вариации |
SS |
df |
MS |
F |
P-Значение |
F критическое |
Выборка
|
|
|
|
|
|
|
Столбцы
|
|
|
|
|
|
|
Взаимодействие
|
|
|
|
|
|
|
Внутри
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итого |
|
|
|
|
|
|
