
- •Содержание
- •2 Литература
- •3 Общие методические указания к решению задач и выполнению контрольных работ
- •4 Основные формулы
- •5 Таблицы вариантов
- •6 Задачи для контрольных работ
- •Приложения
- •Основные физические постоянные
- •Некоторые астрономические величины
- •Плотность твёрдых тел
- •Плотность жидкостей
- •Показатель преломления
- •Работа выхода электронов
- •Относительные атомные массы (округлённые значения) Аr и порядковые номера z некоторых элементов
- •Массы атомов лёгких изотопов
- •Период полураспада радиоактивных изотопов
6 Задачи для контрольных работ
Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением s = A + Bt2, где A = 8 м, B = –2 м/с2. Определить момент времени, когда нормальное ускорение an точки равно 9 м/с2. Найти скорость v, тангенциальное a и полное a ускорение точки в тот же момент времени.
Две материальные точки движутся согласно уравнениям
 и
и
 ,
где A1 = 4 м/с,
B1 = 8 м/с2,
С1 = = –16 м/с3,
A2 = 2 м/с,
B2 = –4 м/с2,
С2 = 1 м/с3.
В какой момент времени ускорения этих
точек будут одинаковы? Найти скорости
v1 и v2
точек в этот момент времени.
,
где A1 = 4 м/с,
B1 = 8 м/с2,
С1 = = –16 м/с3,
A2 = 2 м/с,
B2 = –4 м/с2,
С2 = 1 м/с3.
В какой момент времени ускорения этих
точек будут одинаковы? Найти скорости
v1 и v2
точек в этот момент времени.Тело брошено вертикально вверх с начальной скоростью v0 = 4 м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью v0 вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.
Материальная точка движется прямолинейно с ускорением a = 5 м/с². Определить, на сколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять v0 = 0.
Две автомашины движутся по дорогам, угол между которыми α = 60°. Скорость автомашин v1 = 54 км/ч и v2 =72 км/ч. С какой скоростью v удаляются машины одна от другой?
Материальная точка движется прямолинейно с начальной скоростью v0 = 10 м/с и постоянным ускорением a = –5 м/с. Определить, во сколько раз путь Δs, пройденный материальной точкой, будет превышать модуль ее перемещения Δr спустя t = 5 с после начала отсчета времени.
Точка движется по кривой согласно уравнению
 ?
в котором все величины заданы в единицах
СИ. Найти среднюю скорость движения
точки в промежутке времени от t1 = 2 с
до t2 = 6 с.
?
в котором все величины заданы в единицах
СИ. Найти среднюю скорость движения
точки в промежутке времени от t1 = 2 с
до t2 = 6 с.Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью v1 = 18 км/ч. Далее половину оставшегося пути он ехал со скоростью v2 = 22 км/ч, после чего до конечного пункта он шел пешком со скоростью v3 = 5 км/ч. Определить среднюю скорость <v> велосипедиста.
Первую половину времени автомобиль двигался со скоростью v1 = 20 м/с под углом 1 = 60 к заданному направлению, а вторую – под углом 2 = 120 со скоростью v2 = 40 м/с. Найти среднюю скорость автомобиля на всем перемещении.
Тело брошено под углом α = 30° к горизонту со скоростью v0 = 30 м/с. Каковы будут нормальные an и тангенциальные a
 ускорения тела через время t=1
c после начала
движения?
ускорения тела через время t=1
c после начала
движения?Материальная точка движения по окружности с постоянной угловой скоростью ω = π/6 рад/с. Во сколько раз путь Δs, пройденный точкой за время t = 4 с, будет больше модуля ее перемещения Δr? Принять, что в момент отсчета времени радиус – вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол φ0=π/3 рад.
Материальная точка движется в плоскости xy согласно уравнениям x =A1+B1t+C1t² и y=A2+B2t+C2t², где B1=7 м/с, С1= –2 м/с, В2= –1 м/с, С2=0,2 м/с². Найти модули скорости и ускорения точки в момент времени t = 5 с.
По краю равномерно вращающейся с угловой скоростью ω = 1 рад/с платформы идет человек и обходит платформу за время t = 9,9 с. Каково наибольшее ускорение a движения человека относительно Земли? Принять радиус платформы R=2 м.
Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением ε. Определить тангенциальное ускорение a точки, если известно, что за время t=4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение an =2,7 м/с².
Маховик вращается равноускоренно. Найти угол , который составляет вектор полного ускорения любой точки маховика с радиусом в тот момент, когда маховик совершит первые N = 2 оборота.
При горизонтальном полете со скоростью v = 250 м/с снаряд массой m=8 кг разорвался на две части. Большая часть массой m = 6 кг получила скорость v1 = 400 м/с в направлении полета снаряда. Определить модуль и направление скорости v2 меньшей части снаряда.
С тележки, свободно движущийся по горизонтальному пути со скоростью v1 = 3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной u1= 4 м/с. Определить горизонтальную составляющую скорости v2x человека при прыжке относительно тележки. Масса тележки m1= 210 кг, масса человека m2 = 70 кг.
Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α=30° к линии горизонта. Определить скорость u2 отката платформы, если снаряд вылетает со скоростью u1= 480 м/с. Масса платформы с орудием и снарядами m2=18т, масса снаряда m1 = 60 кг.
Человек массой m1 = 70 кг, бегущий со скоростью v1 = 9 км/ч, догоняет тележку массой m2= 190 кг, движущуюся со скоростью v2 = 3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал на встречу тележки?
Конькобежец, стоя на коньках на льду, бросает камень массой m1=2,5 кг под углом α=30° к горизонту со скоростью v =10 м/с. Какова будет начальная скорость v0 движения конькобежца, если масса его m2=60 кг? Перемещением конькобежца во время броска пренебречь.
На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m1= 60 кг, масса доски m2=20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) v = 1 м/с? Массой колес и трением пренебречь.
Снаряд, летевший со скоростью v = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью u1=150 м/с. Определить скорость u2 большего осколка.
Две одинаковые лодки массами m=200 кг каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу с одинаковыми скоростями v = 1 м/с. Когда лодки поравнялись, то с первой лодки на вторую и со второй на первую одновременно перебрасывают грузы массами m1=20 кг. Определить скорости u1 и u2 лодок после перебрасывания грузов.
На сколько переместится относительно берега лодка длинной l=3,5 м и массой m1=200 кг, если стоящий на корме человек массой m2= 80 кг переместится на нос лодки? Считать лодку расположенной перпендикулярной берегу.
Лодка длинной l=3 м и массой m=120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m1=60 кг и m2=90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?
В лодке массой M = 240 кг стоит человек массой m = 60 кг. Лодка плывет со скоростью v = 2 м/с.Человек прыгает с лодки в горизонтальном направлении со скоростью u = 4 м/с (относительно лодки). Найти скорость лодки после прыжка человека: 1) вперед по движению; 2) в сторону, противоположную движению лодки.
Человек, стоящий на лодке, сделал шесть шагов вдоль нее и остановился. На сколько шагов передвинулась лодка, если масса лодки в два раза больше (меньше) массы человека?
Тело массы M = 990 г лежит на горизонтальной поверхности. В него попадает пуля массы m = 10 г и застревает в нем. Скорость пули v = 700 м/с и направлена горизонтально. Какой s пройдет тело до остановки? Коэффициент трения между телом и поверхностью k = 0,05.
Падающий вертикально шарик массы m = 200 г ударился об пол со скоростью v = 5 м/с и подпрыгнул на высоту h = 46 см. Найти изменение ∆р импульса шарика при ударе.
Тело массой m1 = 2 кг движется навстречу второму телу массой m2 = 1,5 кг и неупруго соударяется с ним. Скорости тел непосредственно перед ударом были v1 = 1 м/с и v2 = 2 м/с. Какое время будут двигаться эти тела послу удара, если коэффициент трения k = 0,05?
В деревянный шар массой m1=8 кг, подвешенный на нити длинной l=1,8 м, попадает горизонтально летящая пуля массой m2=4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонились от вертикали на угол =3°? Размером шара пренебречь, удар пули считать прямым, центральным.
По небольшому куску мягкого железа, лежащему на наковальне массой m1=300 кг, ударяет молот массой m2=8 кг. Определить КПД удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.
Шар массой m1=1 кг движется со скоростью v1 = 4 м/с и сталкивается с шаром массой m2=2 кг, движущимся навстречу ему со скоростью v2 = 3 м/с. Каковы скорости u1 и u2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
Шар массой m1=3 кг движется со скоростью v1 = 2 м/с и сталкивается с покоящимся шаром массой m2=5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
Определить КПД η неупругого удара бойка массой m1=0,5 т, падающего на сваю массой m2=120 кг. Полезной считать энергию, потраченную на вбивание сваи.
Шар массой m1=4 кг движется со скоростью v1 = 5 м/с и сталкивается с шаром массой m2=6 кг, движущимся навстречу ему со скоростью v2 = 2 м/с. Определить каковы скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
Из ствола автоматического пистолета вылетела пуля массой m1= 10 г со скоростью v = 300 м/с. Затвор пистолета массой m2=200 г прижимается пружиной, жесткость которой k=25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.
Шар массой m1=5 кг движется со скоростью v1 =1 м/с и сталкивается с покоящимся шаром массой m2=2 кг. Определить каковы скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью v1 = 600 м/с, а когда орудию дали возможность откатываться назад, снаряд вылетел со скоростью v2 = 580 м/с. С какой скоростью откатилось при этом орудие?
Шар массой m1=2 кг сталкивается с шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу m2 большего шара. Удар считать абсолютно упругим, прямым, центральным.
Определить работу растяжения двух соединенных последовательно пружин жесткостями k1=400 Н/м и k2=250 Н/м, если первая пружина при этом растянулась на Δl = 2 см.
Из шахты глубиной h = 600 м поднимают клеть массой m1=3 т на канате, каждый метр которого имеет массу m = 1,5 кг. Какая работа А совершается при поднятии клетки на поверхность Земли? Каков коэффициент полезного действия η подъемного устройства?
Пружина жесткостью k=500 Н/м сжата силой F = 100 Н. Определить работу А внешней силы, дополнительно сжимающей пружину еще на Δl = 2 см.
Две пружины жесткостью k1=0,5 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации Δl = 4 см.
Какую нужно совершить работу А, чтобы пружину жесткостью k = 800 Н/м, сжатую на х = 6 см, дополнительно сжать на Δх = 8 см?
На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой п1=8 мин-1 стоит человек массой m1 = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n2 = 10 мин-1. Определить массу т2 платформы. Момент инерции человека рассчитывать как для материальной точки.
По касательной к шкиву маховика в виде диска диаметром D = 75 см и массой m = 40 кг приложена сила F = 1 кН. Определить угловое ускорение ε и частоту вращения n маховика через время t = 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.
На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3 с приобрел угловую скорость ω=9 рад/с.
Нить с привязанными к ее концам грузами массами m1 = 50 г и m2 = 60 г перекинута через блок диаметром D = 4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение ε = 1,5 рад/с². Трением и проскальзыванием по блоку нити пренебречь.
Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению φ = At+Bt³, где A = 2 рад/с, В = 0,2 рад/с³. Определить вращающий момент М, действующий на стержень через время t =2 с после начала вращения, если момент инерции стержня J = 0,048 кг·м².
По горизонтальной плоскости катиться диск со скоростью v = 8м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился пройдя путь s = 18 м.
Определить момент силы M, который необходимо приложить к блоку, вращающемуся с частотой n = 12 с-¹, чтобы он остановился в течение времени Δt =8 с. Диаметр блока D = 30 см. Массу блока m = 6 кг считать равномерно распределенной по ободу.
Блок, имеющий форму диска массой m=0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами m1 = 0,3 кг и m2 = 0,7 кг. Определить силы натяжения Т1 и Т2 нити по обе стороны блока.
К краю стола прикреплен блок. Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, а другой – вдоль вертикали вниз. Определить коэффициент f трения между поверхностями груза и стола, если массы каждого груза и масса блока одинаковы и грузы движутся с ускорением a = 5,6 м/с². Проскальзыванием нити по блоку и силой трения, действующей на блок, пренебречь.
К концам легкой и нерастяжимой нити, перекинутой через блок подвешены грузы массами m1= 0,2 кг и m2 = 0,3 кг. Во сколько раз отличаются силы, действующие на нить по обе стороны от блока, если масса блока m = 0,4 кг, а его ось движется вертикально вверх с ускорением a = 2 м/с²? Силами трения и проскальзыванием нити по блоку пренебречь.
Горизонтальная платформа массой т1=150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой п=8 мин-1. Человек массой т2=70 кг стоит при этом на краю платформы. С какой угловой скоростью ω начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым, однородным диском, а человека – материальной точкой.
На скамье Жуковского стоит человек и держит стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью ω1=4 рад/с. С какой угловой скоростью ω2 будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент вращения человека и скамьи J=5 кг·м². Длинна стержня l=1,8 м, масса m=6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.
Платформа в виде диска диаметром D=3 м и массой m1=180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться эта платформа, если по ее краю пойдет человек массой m2=70 кг со скоростью v = 1,8 м/с относительно платформы?
Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол φ повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную (на платформе точку) точку? Масса платформы m1=280 кг, масса человека m2=80 кг.
На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью ω1=25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского. С какой скоростью ω2 станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол =90? Момент инерции человека и скамьи J равен 2,5 кгм2, момент инерции колеса J0=0,5 кгм2.
Определить напряжение G гравитационного поля на высоте h=1000 км над поверхностью Земли. Считать известным ускорение g свободного падения у поверхности Земли и ее радиус R.
Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой т=2 кг: 1) с высоты h=1000 км; 2) из бесконечности?
Из бесконечности на поверхность Земли падает метеорит массой т=30 кг. Определить работу А, которая при этом будет совершена силами гравитационного поля Земли. Ускорение свободного падения g у поверхности Земли и ее радиус считать известными.
С поверхности Земли вертикально вверх пущена ракета со скоростью v = 5 км/с. На какую высоту она поднимется?
По круговой орбите вокруг Земли обращается спутник с периодом Т=90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус считать известными.
На каком расстоянии от центра Земли находится точка, в которой напряженность суммарного гравитационного поля Земли и Луны равна нулю? Принять, что масса Земли в 81 раз больше массы Луны и что расстояние от центра Земли до центра Луны равно 60 радиусам Земли.
Спутник обращается вокруг Земли по круговой орбите на высоте h=520 км. Определить период обращения спутника. Ускорение свободного падения g у поверхности Земли и ее радиус считать известными.
Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте h=1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус считать известными.
Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84108 м?
Во сколько раз средняя плотность земного вещества отличается от средней плотности лунного? Принять, что радиус Rз Земли в 390 раз больше радиуса Rл Луны и вес тела на Луне в 6 раз меньше веса тела на Земле.
Звездная система состоит из двух одинаковых звезд, находящихся на расстоянии r =
 м
друг от друга. Найти период Т обращения
звезд вокруг общего центра масс, если
масса каждой звезды m
=
м
друг от друга. Найти период Т обращения
звезд вокруг общего центра масс, если
масса каждой звезды m
= кг.
кг.Искусственный спутник обращается вокруг Земли по круговой орбите на высоте H = 3200 км над поверхностью Земли. Определить линейную скорость спутника.
На какую часть уменьшается вес тела на экваторе вследствие вращения Земли вокруг оси?
Три материальных точки массой m расположены в вершинах правильного треугольника, сторона которого равна a. Найти гравитационную силу, действующую на одну из масс со стороны двух других.
Спутник, движущийся по круговой орбите радиуса R = 2104 км в экваториальной плоскости Земли с Запада на Восток, появляется над некоторым пунктом на экваторе через каждые = 11,6 ч. Вычислить на сновании этих данных массу Земли. Гравитационная постоянная предполагается известной.
На стержне длиной l=30 см укреплены два одинаковых грузика: один – в середине стержня, другой – на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т простых гармонических колебаний данного физического маятника. Массой стержня пренебречь.
Точка участвует в двух взаимно перпендикулярных колебаниях, уравнения которых x=A1sin ω1t и y=A2cos ω2t, где A1=8 см, A2=4 см, ω1 = = ω2 = 2 с-1. Написать уравнение траектории и построить ее. Показать направление движения точки.
Точка совершает простые гармонические колебания, уравнение которых x=A sinωt , где А=5 см, ω=2 с-1. В момент времени, когда точка обладала потенциальной энергией Ep=0,1 мН, на нее действовала возвращающая сила F = 5 мН. Найти этот момент времени t.
Определить частоту
 простых гармонических колебаний диска
радиусом R=20 см
около горизонтальной оси, проходящей
через середину радиуса диска
перпендикулярно его плоскости.
простых гармонических колебаний диска
радиусом R=20 см
около горизонтальной оси, проходящей
через середину радиуса диска
перпендикулярно его плоскости.Определить период Т простых гармонических колебаний диска радиусом R=40 см около горизонтальной оси, проходящей через образующую диска.
Определить период Т колебаний математического маятника, если его модуль максимального перемещения ∆r=18 см и максимальная скорость vmax = 16 см/с.
Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение x0=4 см, а скорость v0 = 10 см/с. Определить амплитуду А и начальную фазу
 колебаний, если их период Т=2 с.
колебаний, если их период Т=2 с.Складываются два колебания одинакового направления и одинакового периода: x1=A1sin ω1t и х2=A2sin ω2(t+ ), где A1=A2=3 см, ω1=ω2=
 с-1,
=0,5
с. Определить амплитуду А и
начальную фазу
результирующего колебания. Написать
его уравнение. Построить векторную
диаграмму для момента времени t=0.
с-1,
=0,5
с. Определить амплитуду А и
начальную фазу
результирующего колебания. Написать
его уравнение. Построить векторную
диаграмму для момента времени t=0.На гладком горизонтальном столе лежит шар массой М=200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k=500 Н/м. В шар попадает пуля массой т=10 г, летящая со скоростью v = 300 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А и период Т колебаний шара.
Шарик массой т=60 г колеблется с периодом Т=2 с. В начальный момент времени смещение шарика х0=4,0 см и он обладает энергией Е =0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон сохранения возвращающей силы с течением времени.
Точка совершает гармонические колебания, уравнение которых имеет вид x = Asinωt, где A = 5 см, = 2 с–1. Найти ближайший момент времени, в который потенциальная энергия очки П = 10–4 Дж, а возвращающая сила F=+510–3 Н. Определить также фазу колебаний в этот момент времени.
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = A1cosω1t и y = A2cosω2(t + ), где A1 = 4 см, ω1 = с-1, A2 = 8 см, ω1 = с-1, = 1 с. Найти уравнение траектории и начертить ее с соблюдением масштаба.
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = 2 sint и y = –cost (смещения даны в сантиметрах). Найти уравнение траектории и начертить ее с соблюдением масштаба. Показать направление движения точки.
Материальная точка совершает гармонические колебания с частотой = 500 Гц и амплитудой A = 0,02 см. Определить среднее значение скорости <v> и ускорения <a> точки на пути от ее крайнего положения до положения равновесия, а также найти максимальные значения этих величин.
Два гармонических колебания, направленных по одной прямой, имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз складываемых колебаний.
В цилиндр длиной
 м, заполненный воздухом при
нормальном атмосферном давлении
м, заполненный воздухом при
нормальном атмосферном давлении
 ,
начал медленно вдвигать поршень
площадью основания
,
начал медленно вдвигать поршень
площадью основания
 см2. Определить силу F,
действующую на поршень, если его
остановить на расстоянии
см2. Определить силу F,
действующую на поршень, если его
остановить на расстоянии
 см
от дна цилиндра.
см
от дна цилиндра.В баллоне находится газ при температуре
 К. До какой температуры
К. До какой температуры
 надо нагреть газ, чтобы его давление
увеличилось в 1,5 раза?
надо нагреть газ, чтобы его давление
увеличилось в 1,5 раза?Баллон вместимостью
 л заполнен азотом при температуре
л заполнен азотом при температуре
 К.
Когда часть газа израсходовали, давление
в баллоне понизилось на
К.
Когда часть газа израсходовали, давление
в баллоне понизилось на
 кПа. Определить массу m
израсходованного газа. Процесс считать
изотермическим.
кПа. Определить массу m
израсходованного газа. Процесс считать
изотермическим.В баллоне вместимостью
 л находится аргон под давлением
л находится аргон под давлением
 кПа и при температуре
кПа и при температуре
 К. Когда из баллона было взято
некоторое количество газа, давление
в баллоне понизилось до
К. Когда из баллона было взято
некоторое количество газа, давление
в баллоне понизилось до
 кПа, а температура установилась
кПа, а температура установилась
 К. Определить массу m
аргона, взятого из баллона.
К. Определить массу m
аргона, взятого из баллона.Два сосуда одинакового объема содержат кислород. В одном сосуде давление
 МПа и температура
МПа и температура
 К, в другом
К, в другом
 МПа,
МПа,
 К.
Сосуды соединили трубкой и охладили
находящийся в них кислород до температуры
К.
Сосуды соединили трубкой и охладили
находящийся в них кислород до температуры
 К.
Определить установившееся в сосудах
давление р.
К.
Определить установившееся в сосудах
давление р.Вычислить плотность
 азота, находящегося в баллоне под
давлением
азота, находящегося в баллоне под
давлением
 МПа и имеющего температуру
К.
МПа и имеющего температуру
К.Определить относительную молекулярную массу
 газа, если при температуре
газа, если при температуре
 К
и давлении
К
и давлении
 МПа он имеет плотность
МПа он имеет плотность
 кг/м3.
кг/м3.При расширении 10–2 м3 гелия, имеющего температуру 1000 К, давление падает с 1106 до 2,5105 Па. Считая процесс адиабатическим, вычислить объем и температуру газа после расширения.
В сосуде вместимостью
 л находится кислород при температуре
л находится кислород при температуре
 К. Когда часть газа израсходовали,
давление в баллоне понизилось на
К. Когда часть газа израсходовали,
давление в баллоне понизилось на
 кПа.
Определить массу
кПа.
Определить массу
 израсходованного кислорода. Процесс
считать изотермическим.
израсходованного кислорода. Процесс
считать изотермическим.Определить плотность водяного пара, находящегося под давлением
 кПа
и имеющего температуру
кПа
и имеющего температуру
 К.
К.Сколько ходов n надо сделать, чтобы при помощи поршневого насоса, захватывающего при каждом ходе объем v = 400 см3 воздуха, откачать воздух из стеклянного баллона, имеющего объем V = 1 л, до давления pn = 102 Па, если первоначальное давление в баллоне p0 = 105 Па? Температуру воздуха считать постоянной.
В баллоне вместимостью V = 15 л находится смесь, содержащая m1 = 10 г водорода, m2 = 54 г водяного пара и m3 = 60 г оксида углерода CO. Температура смеси t = 27. Определить давление.
Найти молярную массу воздуха, считая, что он состоит по массе из одной части кислорода и трех частей азота.
Найти плотность смеси кислорода массой m1 = 64 г и азота массой m2 = 56 г при температуре t = 27 C и давлении p = 105 Па.
При температуре t = 35 C и давлении p = 708 кПа плотность некоторого газа = 12,2 кг/м3. Определить относительную молекулярную массу Mr газа.
Определить внутреннюю энергию
 водорода, а также среднюю кинетическую
энергию
водорода, а также среднюю кинетическую
энергию
 молекулы этого газа при температуре
К,
если количество вещества
молекулы этого газа при температуре
К,
если количество вещества
 этого газа равно 0,5 моль.
этого газа равно 0,5 моль.Определить суммарную кинетическую энергию
 поступательного движения всех молекул
газа, находящегося в сосуде вместимостью
поступательного движения всех молекул
газа, находящегося в сосуде вместимостью
 л под давлением
л под давлением
 кПа.
кПа.Количество вещества гелия
 моль, температура
моль, температура
 К.
Определить суммарную кинетическую
энергию
поступательного движения всех молекул
этого газа.
К.
Определить суммарную кинетическую
энергию
поступательного движения всех молекул
этого газа.Молярная внутренняя энергия
 некоторого двухатомного газа равна
6,02 кДж/моль. Определить среднюю
кинетическую энергию
некоторого двухатомного газа равна
6,02 кДж/моль. Определить среднюю
кинетическую энергию
 вращательного движения одной молекулы
этого газа. Газ считать идеальным.
вращательного движения одной молекулы
этого газа. Газ считать идеальным.Определить среднюю кинетическую энергию одной молекулы водяного пара при температуре
 К.
К.Определить среднюю квадратичную скорость
 молекулы газа, заключенного в сосуд
вместимостью
молекулы газа, заключенного в сосуд
вместимостью
 л
под давлением
л
под давлением
 кПа.
Масса газа
кПа.
Масса газа
 г.
г.Водород находится при температуре К. Найти среднюю кинетическую энергию вращательного движения одной молекулы, а также суммарную кинетическую энергию Ек всех молекул этого газа; количество водорода
 моль.
моль.При какой температуре средняя кинетическая энергия
 молекулы газа равна
молекулы газа равна
 Дж? Рассмотреть случаи, когда
молекулы газа состоят из одного и
четырех атомов.
Дж? Рассмотреть случаи, когда
молекулы газа состоят из одного и
четырех атомов.В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса каждой пылинки равна
 г.
Газ находится при температуре
К.
Определить средние квадратичные
скорости
,
а также средние кинетические энергии
г.
Газ находится при температуре
К.
Определить средние квадратичные
скорости
,
а также средние кинетические энергии
 поступательного движения молекулы
азота и пылинки.
поступательного движения молекулы
азота и пылинки.Определить среднюю кинетическую энергию поступательного движения и вращательного движения молекулы азота при температуре
 000 К.
Определить также полную кинетическую
энергию Ек молекулы при
тех же условиях.
000 К.
Определить также полную кинетическую
энергию Ек молекулы при
тех же условиях.Средняя квадратичная скорость молекул некоторого газа = 450 м/с. Давление p = 50 кПа. Найти плотность газа при этих условиях.
Какое число молекул N двухатомного газа содержит объем V = 10 см3 при давлении p = 5,3 кПа и температуре t = 27? Какой энергией теплового движения обладают эти молекулы?
Найти полную кинетическую энергию, а также кинетическую энергию вращательного движения одной молекулы аммиака NH3 при температуре t = 27.
Какая часть молекул кислорода при t = 0 обладает скоростями v от 100 до 110 м/с?
Какая часть молекул водорода, находящегося при температуре T = 400 K, обладает скоростями, отличающимися от наиболее вероятной скорости не свыше чем на 5 м/с?
Определить молярную массу М двухатомного газа и его удельные теплоемкости, если известно, что разность
 удельных теплоемкостей этого газа
равна 260 Дж/(кг·К).
удельных теплоемкостей этого газа
равна 260 Дж/(кг·К).Найти удельные
 и
и
 ,
а также молярные
,
а также молярные
 и
и
 теплоемкости углекислого газа.
теплоемкости углекислого газа.Определить показатель адиабаты
 идеального газа, который при температуре
идеального газа, который при температуре
 К
и давлении
К
и давлении
 МПа занимает объем
МПа занимает объем
 л и имеет теплоемкость
л и имеет теплоемкость
 Дж/К.
Дж/К.В сосуде вместимостью
 л находится при нормальных условиях
двухатомный газ. Определить теплоемкость
этого газа при постоянном объеме.
л находится при нормальных условиях
двухатомный газ. Определить теплоемкость
этого газа при постоянном объеме.Определить относительную молекулярную массу и молярную массу М газа, если разность его удельных теплоемкостей
 кДж/(кг·К).
кДж/(кг·К).Определить молярные теплоемкости газа, если его удельные теплоемкости
 кДж/(кг·К)
и
кДж/(кг·К)
и
 кДж/(кг·К).
кДж/(кг·К).Найти удельные и и молярные и теплоемкости азота и гелия.
Вычислить удельные теплоемкости газа, зная, что его молярная масса
 кг/моль и отношение теплоемкостей
кг/моль и отношение теплоемкостей
 .
.Трехатомный газ под давлением
 кПа и температуре
кПа и температуре
 С
занимает объем
С
занимает объем
 л. Определить теплоемкость
этого газа при постоянном давлении.
л. Определить теплоемкость
этого газа при постоянном давлении.Одноатомный газ при нормальных условиях занимает объем
 л.
Вычислить теплоемкость
этого газа при постоянном объеме.
л.
Вычислить теплоемкость
этого газа при постоянном объеме.Смесь газа состоит из кислорода O2 с массовой долей 1 = 85% и озона O3 с массовой долей 2 = 15%. Определить удельные теплоемкости cv и cp этой газовой смеси.
Плотность некоторого двухатомного газа при нормальных условиях = 1,43 кг/м3. Найти удельные теплоемкости cv и cp этого газа.
Вычислить удельные теплоемкости cv и cp смеси неона и водорода, если массовые доли неона и водорода составляют 1 = 80% и 2 = 20%.
Найти молярную массу и число степеней свободы молекул газа, если его удельные теплоемкости cv = 0,65 Дж/(гK) и cp = 0,91 Дж/(гK).
Найти удельные и , а также молярные и теплоемкости хлороводорода.
Определить количество теплоты Q, которое надо сообщить кислороду объемом
 л при его изохорном нагревании,
чтобы давление газа повысилось на
л при его изохорном нагревании,
чтобы давление газа повысилось на
 МПа.
МПа.При изотермическом расширении азота при температуре
 К
объем его увеличился в два раза.
Определить: 1) совершенную при расширении
газа работу А; 2) изменение
К
объем его увеличился в два раза.
Определить: 1) совершенную при расширении
газа работу А; 2) изменение
 внутренней энергии; 3) количество
теплоты Q, полученное
газом. Масса азота
внутренней энергии; 3) количество
теплоты Q, полученное
газом. Масса азота
 кг.
кг.При адиабатном сжатии давление воздуха было увеличено от
 кПа
до
кПа
до
 МПа.
Затем при низменном объеме температура
воздуха была понижена до первоначальной.
Определить давление
МПа.
Затем при низменном объеме температура
воздуха была понижена до первоначальной.
Определить давление
 газа в конце процесса.
газа в конце процесса.Кислород массой
 г занимает объем
г занимает объем
 л и находится под давлением
л и находится под давлением
 кПа. При нагревании газ расширился
при постоянном давлении до объема
кПа. При нагревании газ расширился
при постоянном давлении до объема
 л,
а затем его давление возросло до
л,
а затем его давление возросло до
 кПа
при неизменном объеме. Найти изменение
внутренней энергии
газа, совершенную газом работу
кПа
при неизменном объеме. Найти изменение
внутренней энергии
газа, совершенную газом работу
 и теплоту Q, переданную
газу. Построить график процесса.
и теплоту Q, переданную
газу. Построить график процесса.Объем водорода при изотермическом расширении при температуре К увеличился в
 раза. Определить работу А, совершенную
газом, и теплоту Q,
полученную при этом. Масса
водорода равна 200 г.
раза. Определить работу А, совершенную
газом, и теплоту Q,
полученную при этом. Масса
водорода равна 200 г.Азот массой
 кг был изобарно нагрет от температуры
кг был изобарно нагрет от температуры
 К до температуры
К до температуры
 К. Определить работу А, совершенную
газом, полученную им теплоту Q
и изменение
внутренней энергии азота.
К. Определить работу А, совершенную
газом, полученную им теплоту Q
и изменение
внутренней энергии азота.Во сколько раз увеличится объем водорода, содержащий количество вещества
 моль при изотермическом расширении,
если при этом газ получит количество
теплоты
моль при изотермическом расширении,
если при этом газ получит количество
теплоты
 Дж?
Температура водорода
К.
Дж?
Температура водорода
К.Какая работа А совершается при изотермическом расширении водорода массой
 г, взятого при температуре
г, взятого при температуре
 К, если объем газа увеличивается
в три раза?
К, если объем газа увеличивается
в три раза?При изобарическом сжатии азота была совершена работа, равная 12 кДж. Определить количество теплоты и изменение внутренней энергии газа.
При адиабатическом сжатии 6 кг сероводорода, занимающего объем 3 м3 при температуре 300 К, его давление увеличилось в 2 раза. Определить работу сжатия и изменение внутренней энергии газа.
Для нагревания 10 г неизвестного газа на 1 К при постоянном давлении требуется 9,12 Дж, при постоянном объеме 6,49 Дж. Что это за газ?
Два моля идеального (одноатомного) газа, находящегося при 0°С, сначала изохорически перевели в состояние, в котором давление в два раза больше первоначального, а затем изобарически в состояние, в котором объем в два раза больше первоначального. Найти изменение внутренней энергии газа.
Один моль аргона расширили по политропе с показателем n = 1,5. При этом температура газа испытала приращение T = –26 K. Найти количество полученного газом тепла, и работу, совершенную газом.
Воздух сжимают один раз изотермически, а другой – адиабатически. Определить отношение работ сжатия газа, если в обоих случаях его объем уменьшается в N = 2 раза.
Какое количество теплоты надо сообщить смеси газов, отстоящей из m1 = 100 г водорода и m2 = 200 г гелия, для ее изохорного нагревания на T = 10 С?
Идеальный газ совершает цикл Карно при температурах теплоприемника
 К
и теплоотдатчика
К.
Во сколько раз увеличится коэффициент
полезного действия
К
и теплоотдатчика
К.
Во сколько раз увеличится коэффициент
полезного действия
 цикла, если температура теплоотдатчика
возрастет до
цикла, если температура теплоотдатчика
возрастет до
 К?
К?Идеальный газ совершает цикл Карно. Температура
 теплоотдатчика в четыре раза (
теплоотдатчика в четыре раза ( )
больше температуры теплоприемника.
Какую долю
)
больше температуры теплоприемника.
Какую долю
 количества теплоты, полученного за
один цикл от теплоотдатчика, газ отдаст
теплоприемнику?
количества теплоты, полученного за
один цикл от теплоотдатчика, газ отдаст
теплоприемнику?Определить работу
 изотермического сжатия газа, совершающего
цикл Карно, КПД которого
изотермического сжатия газа, совершающего
цикл Карно, КПД которого
 ,
если работа изотермического расширения
равна
,
если работа изотермического расширения
равна
 Дж.
Дж.Газ, совершающий цикл Карно, отдал теплоприёмнику теплоту
 кДж. Определить температуру
теплоотдатчика, если при температуре
теплоприемника
кДж. Определить температуру
теплоотдатчика, если при температуре
теплоприемника
 К работа цикла
К работа цикла
 кДж.
кДж.Газ, являясь рабочим веществом в цикле Карно, получил от теплоотдатчика теплоту
 кДж и совершил работу
кДж и совершил работу
 кДж. Определить температуру
теплоотдатчика, если температура
теплоприемника
кДж. Определить температуру
теплоотдатчика, если температура
теплоприемника
 К.
К.Газ, совершающий цикл Карно, отдал теплоприёмнику 67% теплоты, полученной от теплоотдатчика. Определить температуру теплоприемника, если температура теплоотдатчика
 К.
К.Во сколько раз увеличится коэффициент полезного действия цикла Карно при повышении температуры теплоотдатчика от
 К до
К до
 К? Температура теплоприемника
К.
К? Температура теплоприемника
К.Найти изменение энтропии в процессе изобарического нагревания 1 кмоль азота от 0 до 120 C.
Найти изменение энтропии в процессе изохорического охлаждения 2 кмоль кислорода от 500 до 250 К.
Найти изменение энтропии в процессе изотермического расширения 1 кмоль углекислого газа от объема 10 до 30 м3.
При изотермическом расширении одного киломоля газа его давление уменьшается в 2 раза. Определить изменение энтропии.
Один киломоль азота при 400 К и два киломоля кислорода при температуре 300 К смешивают при постоянном давлении, равном 105 Па. Определить изменение энтропии в этом процессе.
В двух сосудах одного и того же объема находятся различные идеальные газы (водород и кислород). Масса первого газа m1 = 100 г, второго – m2 = 100 г. Давления и температуры газов одинаковы. Сосуды соединяют, и начинается процесс диффузии. Определить изменение энтропии рассматриваемой системы.
Кислород массой 1 кг занимает объем V0. Определить вероятность самопроизвольного изотермического сжатия кислорода на 10–6 часть первоначального объема.
640 г расплавленного свинца при температуре плавления вылили на лед при 0 C. Найти изменение энтропии при этом процессе.
Какова средняя арифметическая скорость
 молекул кислорода при нормальных
условиях, если известно, что средняя
длина свободного пробега
молекул кислорода при нормальных
условиях, если известно, что средняя
длина свободного пробега
 молекулы кислорода при этих условиях
равна 100 нм?
молекулы кислорода при этих условиях
равна 100 нм?В сосуде вместимостью л находится водород массой
 г. Определить среднюю длину
свободного пробега
молекулы водорода в этом сосуде.
г. Определить среднюю длину
свободного пробега
молекулы водорода в этом сосуде.Средняя длина свободного пробега молекулы водорода при некоторых условиях равна 2 мм. Найти плотность водорода при этих условиях.
Водород находится под давлением
 мкПа и имеет температуру
К. Определить среднюю длину
свободного пробега
молекулы такого газа.
мкПа и имеет температуру
К. Определить среднюю длину
свободного пробега
молекулы такого газа.Кислород находится под давлением
 нПа при температуре
К.
Вычислить среднее число
нПа при температуре
К.
Вычислить среднее число
 столкновений молекулы кислорода при
этих условиях за время
столкновений молекулы кислорода при
этих условиях за время
 с.
с.При каком давлении р средняя длина свободного пробега молекул азота равна 1 м, если температура газа
 °С?
°С?Найти среднее число столкновений за время
 с и длину свободного пробега
молекулы гелия, если газ находится под
давлением
кПа
при температуре
К.
с и длину свободного пробега
молекулы гелия, если газ находится под
давлением
кПа
при температуре
К.Найти массу m воды, вошедшей в стеклянную трубку с диаметром канала
 мм, опущенную в воду на малую
глубину. Считать смачивание полным.
мм, опущенную в воду на малую
глубину. Считать смачивание полным.Какую работу А надо совершить при выдувании мыльного пузыря, чтобы увеличить его объем от
 см3 до
см3 до
 см3? Считать процесс
изотермическим.
см3? Считать процесс
изотермическим.Пространство между двумя стеклянными параллельными пластинками с площадью поверхности
 см2 каждая, расположенными
на расстоянии
см2 каждая, расположенными
на расстоянии
 мкм друг от друга, заполнено водой.
Определить силу F,
прижимающую пластинки друг к другу.
Считать мениск вогнутым с диаметром
d, равным расстоянию
между пластинками.
мкм друг от друга, заполнено водой.
Определить силу F,
прижимающую пластинки друг к другу.
Считать мениск вогнутым с диаметром
d, равным расстоянию
между пластинками.Глицерин поднялся в капиллярной трубке диаметром канала
 мм на высоту
мм на высоту
 мм. Определить поверхностное
натяжение
мм. Определить поверхностное
натяжение
 глицерина. Считать смачивание полным.
глицерина. Считать смачивание полным.В воду опущена на очень малую глубину стеклянная трубка с диаметром канала мм. Определить массу воды, вошедшей в трубку.
На сколько давление р воздуха внутри мыльного пузыря больше нормального атмосферного давления , если диаметр пузыря
 мм?
мм?Воздушный пузырек диаметром
 мкм находится в воде у самой ее
поверхности. Определить плотность
воздуха в пузырьке, если воздух над
поверхностью воды находится при
нормальных условиях.
мкм находится в воде у самой ее
поверхности. Определить плотность
воздуха в пузырьке, если воздух над
поверхностью воды находится при
нормальных условиях.Две капли ртути радиусом
 мм каждая слились в одну большую
каплю. Определить энергию
мм каждая слились в одну большую
каплю. Определить энергию
 ,
которая выделится при этом слиянии.
Считать процесс изотермическим.
,
которая выделится при этом слиянии.
Считать процесс изотермическим.
Точечные заряды Q1 = 20 мкКл, Q2 = –10 мкКл находятся на расстоянии d = 5 см. друг от друга. Определить напряженность поля в точке, удаленной на r1 = 3 см от первого и на r2 = 4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд Q = 1 мкКл.
Три одинаковых точечных заряда Q1 = Q2 = Q3 = 2 нКл находятся в вершинах равностороннего треугольника со сторонами а = 10 см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.
Два положительных точечных заряда Q и 9Q закреплены на расстоянии d = 100 см. друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол
 .
Шарики погружают в масло. Какова
плотность
.
Шарики погружают в масло. Какова
плотность
 масла, если угол расхождения нитей при
погружении в масло остается неизменным?
Плотность материала шариков
масла, если угол расхождения нитей при
погружении в масло остается неизменным?
Плотность материала шариков
 кг/м3, диэлектрическая
проницаемость масла
кг/м3, диэлектрическая
проницаемость масла
 = 2,2.
= 2,2.Четыре одинаковых заряда Q1 = Q2 = Q3 = Q4 = 40 нКл закреплены в вершинах квадрата со стороной а = 10 см. Найти силу F, действующую на один из этих зарядов со стороны трех остальных.
Точечные заряды Q1 = 30 мкКл и Q2 = –20 мкКл находятся на расстоянии d = 20 см друг от друга. Определить напряженность электрического поля Е в точке, удаленной от первого заряда на расстояние r1 = 30 см, а от второго – на r2 = 15 см.
В вершинах правильного треугольника со стороной а = 10 см. Находятся заряды Q1 = 10 мкКл, Q2 = 20 мкКл и Q3 = 30 мкКл. Определить силу F, действующую на заряд Q1 со стороны двух других зарядов.
В вершинах квадрата находятся одинаковые заряды Q1 = Q2 = Q3 = Q4 = 810-10 Кл. Какой отрицательный заряд Q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?
На расстоянии d = 20 см находятся два точечных электрических заряда: Q1 = –50 нКл и Q2 = 100 нКл. Определить силу F, действующую на заряд Q3 = –10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.
Расстояние d между двумя точечными зарядами Q1 = 2 нКл и Q2 = 4 нКл равно 60 см. Определить точку, в которую нужно поместить третий заряд Q3 так, чтобы система зарядов находилась в равновесии. Определить заряд Q3 и его знак. Устойчивое или неустойчивое будет равновесие?
Два шарика массой m = 1 г каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити l = 10 см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол = 60?
Расстояние между зарядами Q1 = 100 нКл и Q2 = –50 нКл равно d = 10 см. Определить силу F, действующую на заряд Q3 = 1 мкКл, отстоящую от r1 = 12 см от заряда Q1 и на r2 = 10 см от заряда Q2.
Два одинаковых положительных точечных заряда Q1 = Q2 = Q находятся на расстоянии 2l = 10 см друг от друга. На прямой, являющейся осью симметрии этих зарядов и перпендикулярной к линии, соединяющей центры зарядов, точку, в которой напряженность поля электрического поля имеет максимум.
Два заряженных шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины и опущены в керосин. Какова должна быть плотность материала шариков, чтобы углы расхождения нитей в воздухе и в керосине были одинаковы?
К заряженной бесконечной плоскости, расположенной вертикально, присоединен на нити заряженный шарик с массой m = 1 г и зарядом Q = 1 нКл. Какой угол с плоскостью образует нить, на которой весит шарик, если на поверхности равномерно распределен заряд с поверхностной плотностью = 40 мкКл/м2?
Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд
 мкКл/м. Определить напряженность
Е электрического поля, создаваемого
распределенным зарядом в точке А,
лежащей на оси стержня на расстоянии
а = 20 см. от его конца.
мкКл/м. Определить напряженность
Е электрического поля, создаваемого
распределенным зарядом в точке А,
лежащей на оси стержня на расстоянии
а = 20 см. от его конца.Тонкое кольцо несет распределенный заряд Q = 0,2 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см. Радиус кольца R = 10 см.
Треть тонкого кольца радиуса R = 10 см несет распределенный заряд Q = 50 нКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью
 мкКл/м.
Определить напряженность Е
электрического поля, создаваемого
распределенным зарядом в точке А,
лежащей на оси стержня на расстоянии
а = 20 см от его начала.
мкКл/м.
Определить напряженность Е
электрического поля, создаваемого
распределенным зарядом в точке А,
лежащей на оси стержня на расстоянии
а = 20 см от его начала.По тонкому кольцу радиусом R = 20 см. равномерно распределен с линейной плотностью
 мкКл/м заряд. Определить
напряженность Е электрического
поля, создаваемого распределенным
зарядом в точке А, находящейся на
оси кольца на расстоянии h = 2R
от его центра.
мкКл/м заряд. Определить
напряженность Е электрического
поля, создаваемого распределенным
зарядом в точке А, находящейся на
оси кольца на расстоянии h = 2R
от его центра.На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями
 и
и
 (рис. 1). Требуется: 1) используя теорему
Остроградского–Гаусса, найти зависимость
Е(r) напряженности
электрического поля от расстояния для
трех областей: I, II,
и III. Принять
= 4
(рис. 1). Требуется: 1) используя теорему
Остроградского–Гаусса, найти зависимость
Е(r) напряженности
электрического поля от расстояния для
трех областей: I, II,
и III. Принять
= 4 ,
=
,
=  ;
2) вычислить напряженность Е в
точке, удаленной от центра на расстояние
r, и указать направление
вектора
.
Принять
= 30
нКл/м2, r = 1,5R;
3) построить график Е(r).
;
2) вычислить напряженность Е в
точке, удаленной от центра на расстояние
r, и указать направление
вектора
.
Принять
= 30
нКл/м2, r = 1,5R;
3) построить график Е(r).См. условие задачи 3.21. В п.1 принять 1 = , 2 = –. В п.2 принять = 0,1 мкКл/м2, r = 3R
См. условие задачи 3.21. В п.1 принять 1 = –4, 2 = . В п.2 принять = 50 нКл/м2, r = 1,5R.
См. условие задачи 3.21. В п.1 принять 1 = –2, 2 = . В п.2 принять = 0,1 мкКл/м2, r = 3R.
На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями 1 и 2 (рис. 2). Требуется: 1) используя теорему Остроградского – Гаусса и принцип суперпозиции электрических полей, найти выражение Е(х) напряженности электрического поля в трех областях: I, II и III. Принять 1 = 2, 2 = ; 2) вычислить напряженность Е поля в точке, расположенной слева от плоскостей, и указать направление вектора Е; 3) построить график Е(х).

Рисунок 1

Рисунок 2
См. условие задачи 3.25. В п.1 принять 1 = –4, 2 = 2. В п.2 принять = 40 нКл/м2 и точку расположить между плоскостями.
См. условие задачи 3.25. В п.1 принять 1 = , 2 = –2. В п.2 принять = 20 нКл/м2 и точку расположить справа от плоскостей.
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями 1 и 2 (рис. 3). Требуется: 1) используя теорему Остроградского – Гаусса: найти зависимость Е (r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять 1 = –2, 2 = ; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора . Принять = 50 нКл/м2, r = 1,5R; 3) построить график Е (r).

Рисунок 3
См. условие задачи 3.28. В п.1 принять 1 = , 2 = –. В п.2 принять = 60 нКл/м2, r = 3R.
См. условие задачи 3.28. В п.1 принять 1 = –, 2 = 4 . В п.2 принять = 30 нКл/м2, r = 4R.
Два точечных заряда
 нКл
и
нКл
и
 нКл
находятся на расстоянии d = 60
см друг от друга. Какую работу
необходимо совершить внешним силам,
чтобы уменьшить расстояние между
зарядами вдвое?
нКл
находятся на расстоянии d = 60
см друг от друга. Какую работу
необходимо совершить внешним силам,
чтобы уменьшить расстояние между
зарядами вдвое?Электрическое поле создано заряженным проводящим шаром, потенциал
 которого 300 В. Определить работу
сил поля по перемещению заряда Q = 0,2
мкКл из точки 1 в точку 2 (рис. 4).
которого 300 В. Определить работу
сил поля по перемещению заряда Q = 0,2
мкКл из точки 1 в точку 2 (рис. 4).

Рисунок 4
Электрическое поле создано зарядами Q1 = 2 мкКл и Q2 = –2 мкКл, находящимися на расстоянии а = 10 см. друг от друга. Определить работу сил поля, совершаемую при перемещении заряда Q = 0,5 мкКл из точки 1 в точку 2 (рис. 5).

Рисунок 5
Две параллельно заряженные плоскости, поверхностные плотности заряда которых 1 = 2 мкКл/м2 и 2 = –0,8 мкКл/м2, находятся на расстоянии d = 0,6 см. друг от друга. Определить разность потенциалов U между плоскостями.
Диполь с электрическим моментом р = 100 пКлм свободно установился в электрическом поле напряженностью Е = 200 кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол = 180.
Четыре одинаковых капли ртути, заряженных до потенциала = 10 В, сливаются в одну. Каков потенциал 1 образовавшейся капли?
Тонкий стержень согнут в кольцо радиусом R = 10 см. Он равномерно заряжен с линейной плотностью заряда = 800 нКл/м. Определить потенциал в точке, расположенной на оси кольца на расстоянии h = 10 см от его центра.
Поле образовано точечным диполем с электрическим моментом р = 200 пКлм. Определить разность потенциалов U двух точек поля, расположенных симметрично относительно диполя на его оси на расстоянии r = 40 см от центра диполя.
Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой = 20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r1 = 8 см и r2 = 12 см.
Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда = 200 пКл/м. Определить потенциал поля в точке пересечения диагоналей.
Одинаковые заряды q = 100 нКл расположены в вершинах квадрата со стороной а = 10 см. Определите потенциальную энергию той системы.
Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью = 1 нКл/м2. Определите разность потенциалов между двумя точками этого поля, лежащими на расстоянии x1 = 20 см и x2 = 50 см от плоскости.
Электростатическое поле создается шаром радиусом R = 8 см, равномерно заряженным с объемной плотностью = 10 нКл/м3. Определить разность потенциалов между двумя точками этого поля, лежащими на расстоянии r1 = 10 см и r2 = 15 см от центра шара.
Электростатическое поле создается бесконечным цилиндром радиусом R = 8 мм, равномерно заряженным с линейной плотностью = 10 нКл/м. Определить разность потенциалов между двумя точками этого поля, лежащими на расстоянии r1 = 2 мм и r2 = 7 мм от поверхности этого цилиндра.
Электростатическое поле создается сферой радиусом R = 5 см, равномерно заряженной с поверхностной плотностью = 1 нКл/м2. Определить разность потенциалов между двумя точками поля, лежащими на расстояниях r1 = 10 см и r2 = 15 см от центра сферы.
Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом ( = 10 нКл/м). Определить кинетическую энергию Ek1 электрона в точке, находящейся на расстоянии l1 = a от линии, если в точке, удаленной на l2 = 2a от линии его кинетическая энергия Ek2 = 200 эВ.
Электрон, обладавший кинетической энергией Ek = 10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U = 8 В?
Найти отношение скоростей ионов Си++ и К+, прошедших одинаковую разность потенциалов.
Электрон с энергией Ek = 400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Найти минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее Q = –10 нКл.
Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость v = 105 м/с. Расстояние между пластинами d = 8 мм. Найти: 1) разность потенциалов U между пластинами; 2) поверхностную плотность заряда на пластинах.
Пылинка массой т = 5 нг, несущая на себе N = 10 электронов, прошла в вакууме ускоряющую разность потенциалов U = 1 МВ. Какова кинетическая энергия Ek пылинки? Какую скорость v приобрела пылинка?
Какой минимальной скоростью vmin должен обладать протон, чтобы он мог достигнуть поверхности металлического шара, имеющего радиус R и заряженного до потенциала = 400 B, начав двигаться из точки, удаленной на l = 3R от поверхности шара?
В однородное электрическое поле напряженностью Е = 200 В/м влетает (вдоль силовой линии) электрон со скоростью v0 = 2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.
Пылинка массой т = 200 мкг, несущая на себе заряд Q = 40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость v = 10 м/с. Определить скорость v0 пылинки до того, как она влетела в поле.
Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом
 1 = 100
В электрон имел скорость v1 = 6
Мм/с. Определить потенциал
2
точки поля, дойдя до которой электрон
потеряет половину своей скорости.
1 = 100
В электрон имел скорость v1 = 6
Мм/с. Определить потенциал
2
точки поля, дойдя до которой электрон
потеряет половину своей скорости.Электрон, пролетая в электрическом поле, увеличил свою скорость с v1 = 1000 км/с до v2 = 3000 км/с. Найти ускоряющею разность потенциалов.
Два одинаковых заряда q1 = q2 = 50 мкКл находятся на расстоянии r1 = 1 м друг от друга. Какую работу надо совершить, чтобы сблизить их до расстояния r2 = 0,5 м?
Электрон с начальной скоростью v = 3 Мм/с влетел в однородное электрическое поле напряженностью E = 150 В/м. Вектор начальной скорости перпендикулярен линиям напряженности электрического поля. Определить скорость электрона через t = 0,1 мс.
Какую ускоряющую разность потенциалов должен пройти электрон, чтобы получить скорость v = 8 Мм/с?
Протон, летящий к неподвижному ядру двукратно ионизированного атома гелия, на очень большом расстоянии от ядра имеет скорость v0 =104 м/с. На какое расстояние протон сможет приблизиться к ядру, если ядро гелия все время остается неподвижным?
Конденсаторы емкостью С1 = 5 мкФ и С2 = 10 мкФ заряжены до напряжений U1 = 60 В и U2 = 100 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.
Конденсатор емкостью С1 = 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденсатор емкостью С2 = 20 мкФ.
Конденсаторы емкостями С1 = 2 мкФ, С2 = 5 мкФ и С3 = 10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить напряжение и заряд на каждом из конденсаторов.
Два конденсатора емкостями С1 = 2 мкФ и С2 = 5 мкФ заряжены до напряжений U1 = 100 В и U2 = 150 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.
Два одинаковых плоских воздушных конденсатора емкостью С = 100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.
Два конденсатора емкостями С1 = 5 мкФ и С2 = 8 мкФ соединены последовательно и присоединены к батарее с ЭДС
 = 80
В. Определить заряды Q1
и Q2 конденсаторов
и разности потенциалов U1
и U2 между их
обкладками.
= 80
В. Определить заряды Q1
и Q2 конденсаторов
и разности потенциалов U1
и U2 между их
обкладками.
Плоский конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние между пластинами d = 2 мм. Конденсатор присоединен к источнику напряжения U = 80 В. Определить заряд Q и напряженность Е поля конденсатора в двух случаях: а) диэлектрик – воздух; б) диэлектрик – стекло.
Два металлических шарика радиусом R1 = 5 см и R2 = 10 см имеют заряды Q1 = 40 нКл и Q2 = -2 нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводником.
Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: стекла толщиной d1 = 0,2 см и слоем парафина толщиной d2 = 0,2 см. Разность потенциалов между обкладками U = 300 В. Определить напряженность Е поля и падение потенциалов в каждом из слоев.
Плоский конденсатор с площадью пластин S = 200 см2 каждая заряжен до разности потенциалов U = 2 кВ. Расстояние между пластинами d = 2 см. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность энергии поля.
Два проводящих шара с радиусами R1 = 8 см и R2 = 20 см, находящихся на большом расстоянии друг от друга, имели заряды q1 = 40 нКл и q2 = –20 нКл. Каковы будут заряды на шарах после соединения их проводником? Емкостью проводника, соединяющего шары пренебречь.
Два проводящих шара с радиусами R1 = 10 см и R2 = 30 см находятся друг от друга на расстоянии, которое во много раз больше радиуса второго шара. На первый шар помещен заряд q1 = 10 нКл. Каковы будут заряды на шарах после соединения их проводником, если второй шар не был заряжен? Емкостью проводника, соединяющего шары пренебречь.
Конденсатор емкости C1 = 4 мкФ, заряженный до напряжения U1 = 10 В, соединен параллельно с заряженным до напряжения U2 = 20 В конденсатором емкости C2 = 6 мкФ (соединили разноименно заряженные обкладки конденсаторов). Какой заряд окажется на пластинах первого конденсатора после соединении?
Найти количество теплоты, выделившееся при соединении одноименно заряженных конденсаторов C1 = 2 мкФ и C2 = 0,5 мкФ. Разности потенциалов между обкладками конденсаторов U1 = 100 В и U1 = 50 В.
Найти количество теплоты, выделившееся при соединении незаземленных обкладок конденсаторов с емкостями C1 = 2 мкФ и C2 = 0,5 мкФ. Разности потенциалов до соединения между незаземленными обкладками конденсаторов и землей U1 = 100 В и U2 = –5 0 В.
Катушка и амперметр соединены последовательно и подключены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением r = 4 кОм. Амперметр показывает силу тока I = 0,3 А, вольтметр – напряжение U = 120 В. Определить сопротивление R катушки. Определить относительную погрешность , которая будет допущена при измерении сопротивления, если пренебречь силой тока, текущего через вольтметр.
От батареи, ЭДС которой = 600 В, требуется передать энергию на расстояние l = 1 км. Потребляемая мощность Р = 5 кВт. Найти минимальные потери мощности в сети, если диаметр медных проводящих проводов d = 0,5 см.
При внешнем сопротивлении R1 = 8 Ом сила тока в цепи I1 = 0,8 А, при сопротивлении R2 = 15 Ом силы тока I2 = 0,5 А. Определить силу тока Iк.з. короткого замыкания источника ЭДС.
ЭДС батареи = 24 В. Наибольшая сила тока, которую может дать батарея, Imax = 10 A. Определить максимальную мощность Pmax, которая может выделяться во внешней цепи.
Аккумулятор с ЭДС = 12 В заряжается от сети постоянного тока с напряжением U = 15 В. Определить напряжение на клеммах аккумулятора, если его внутреннее сопротивление Ri = 10 Ом.
От источника с напряжением U = 800 В необходимо передать потребителю мощность Р = 10 кВт на некоторое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы потери энергии в ней не превышали 10% от передаваемой мощности?
При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление R обмотки мотора равно 6 Ом.
За время t = 20 c при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Определить скорость нарастания силы тока. Если сопротивление проводника R = 5 Ом.
Сила тока в проводнике (R = 100 Ом) изменяется со временем по закону I = I0e
 ,
где I0 = 20
А, = 102
с–1. Определить количество
теплоты, выделившееся в проводнике за
время t =
10–2 с.
,
где I0 = 20
А, = 102
с–1. Определить количество
теплоты, выделившееся в проводнике за
время t =
10–2 с.Сила тока в проводнике сопротивлением R = 10 Ом за время t = 50 с равномерно нарастает от I1 = 5 А до I2 = 10 А. Определить количество теплоты Q, выделившейся за это время в проводнике.
Сила тока в проводнике изменяется со временем по закону I = I0sin
 .
Найти заряд Q,
проходящий через поперечное сечение
проводника за время t,
равное половине периода Т, если
начальная сила тока I0 = 10 А,
циклическая частота
.
Найти заряд Q,
проходящий через поперечное сечение
проводника за время t,
равное половине периода Т, если
начальная сила тока I0 = 10 А,
циклическая частота
 с-1.
с-1.
За время t = 10 с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты Q = 40 кДж. Определить среднюю силу тока <I> в проводнике, если его сопротивление R = 25 Ом.
За время t = 8 с при равномерно возраставшей силе тока в проводнике сопротивлением R = 8 Ом выделилось количество теплоты Q = 500 Дж. Определить заряд q, проходящий в проводнике, если сила тока в начальный момент времени равна нулю.
Определить количество теплоты Q, выделившееся за время t = 10 c в проводнике сопротивлением R = 10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I1 = 10 А до I2 = 0.
Сила тока в цепи изменяется по закону I = I0 e . Определить количество теплоты, которое выделится в проводнике сопротивлением r = 20 Ом за время, в течение которого ток уменьшится в е раз. Коэффициент принять равным 210–2 с-1.
Бесконечно длинный провод с током
 А изогнут так, как это показано на рис.
6. Определить магнитную индукцию
в точке
А изогнут так, как это показано на рис.
6. Определить магнитную индукцию
в точке
 .
Радиус дуги
.
Радиус дуги
 см.
см.Магнитный момент
 тонкого проводящего кольца
тонкого проводящего кольца
 А·м2.
Определить магнитную индукцию
в точке
,
находящейся на оси кольца и удаленной
от точек кольца на расстояние
А·м2.
Определить магнитную индукцию
в точке
,
находящейся на оси кольца и удаленной
от точек кольца на расстояние
 см (рис. 7).
см (рис. 7).


Рисунок 6 Рисунок 7
По двум скрещенным под прямым углом бесконечно длинным проводам текут токи
 и
и
 (
А). Определить магнитную индукцию
в точке А (рис. 8). Расстояние
(
А). Определить магнитную индукцию
в точке А (рис. 8). Расстояние
 см.
см.По бесконечно длинному проводу, изогнутому так, как это показано на рис. 9, течет ток
 А. Определить магнитную индукцию
в точке О. Радиус дуги
см.
А. Определить магнитную индукцию
в точке О. Радиус дуги
см.


Рисунок 8 Рисунок 9
По тонкому кольцу радиусом
 см течет ток
А. Определить магнитную индукцию
на оси кольца в точке А (рис. 10). Угол
см течет ток
А. Определить магнитную индукцию
на оси кольца в точке А (рис. 10). Угол
 .
.По двум бесконечно длинным проводам, скрещенным под прямым углом, текут токи
 и
и
 (
( А).
Определить магнитную индукцию
в точке А,
равноудаленной от проводов на расстояние
см
(рис. 11).
А).
Определить магнитную индукцию
в точке А,
равноудаленной от проводов на расстояние
см
(рис. 11).

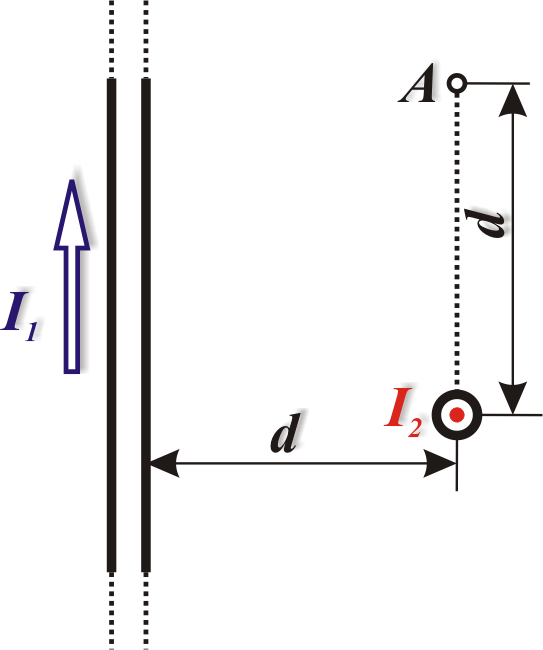
Рисунок 10 Рисунок 11
По бесконечно длинному проводу, изогнутому так, как это показано на рис. 12, течет ток А. Определить магнитную индукцию в точке О. Радиус дуги см.
По тонкому кольцу течет ток
 А.
Определить магнитную индукцию
в точке А, равноудаленной от точек
кольца на расстояние
А.
Определить магнитную индукцию
в точке А, равноудаленной от точек
кольца на расстояние
 см
(рис. 13). Угол
см
(рис. 13). Угол
 .
.


Рисунок 12 Рисунок 13
По двум бесконечно длинным, прямым параллельным проводам текут одинаковые токи
 А. Определить магнитную индукцию
в точке А (рис. 14), равноудаленной
от проводов на расстояние
см.
Угол
.
А. Определить магнитную индукцию
в точке А (рис. 14), равноудаленной
от проводов на расстояние
см.
Угол
.Бесконечно длинный провод с током
 А изогнут так, как это показано на
рис. 15. Определить магнитную индукцию
в точке А, лежащей на биссектрисе
прямого угла на расстоянии
см от его вершины.
А изогнут так, как это показано на
рис. 15. Определить магнитную индукцию
в точке А, лежащей на биссектрисе
прямого угла на расстоянии
см от его вершины.По двум длинным параллельным проводам текут в одинаковом направлении токи I1 = 10 A и I2 = 12 A. Расстояние между проводами a = 10 см. Определить напряженность магнитного поля в точке, удаленной от первого проводника на r1 = 8 см и от второго на r2 = 6 см.


Рисунок 14 Рисунок 15
Решить предыдущую задачу при условии, что токи текут в противоположном направлениях, а точка удалена от первого провода на r1 = 15 см и от второго на r2 = 10 см.
По тонкому проводнику, изогнутому в виде правильного шестиугольника со стороной a = 10 см, идет ток I =20 A. Определить магнитную индукцию в центре шестиугольника.
Два круговых витка радиусом R = 4 см каждый расположены в параллельных плоскостях на расстоянии d = 10 см друг от друга. По виткам в одном направлении текут токи I1 = I2 = 2 A. Найти напряженность магнитного поля на оси витков в точке, находящейся на равном расстоянии от них.
Два круговых витка радиусом R = 2 см каждый расположены в двух взаимно перпендикулярных плоскостях так, что центры этих витков совпадают. По виткам текут токи I1 = I2 = 5 A. Найти напряженность магнитного поля в центре этих витков.
По трем параллельным прямым проводам, находящимся на одинаковом расстоянии
 см
друг от друга, текут одинаковые токи
см
друг от друга, текут одинаковые токи
 А.
В двух проводах направления токов
совпадают. Вычислить для каждого из
проводов отношение силы, действующей
на него, к его длине.
А.
В двух проводах направления токов
совпадают. Вычислить для каждого из
проводов отношение силы, действующей
на него, к его длине.Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи А. Определить силу F, действующую на рамку, если ближайшая к проводу сторона рамки находится от него на расстоянии, равном ее длине.
Тонкий провод длиной
 см изогнут в виде полукольца и
помещен в магнитное поле (
см изогнут в виде полукольца и
помещен в магнитное поле ( мТл) так, что площадь полукольца
перпендикулярна линиям магнитной
индукции. По проводу пропустили ток
А. Определить силу
,
действующую на провод. Подводящие
провода направлены вдоль линий магнитной
индукции.
мТл) так, что площадь полукольца
перпендикулярна линиям магнитной
индукции. По проводу пропустили ток
А. Определить силу
,
действующую на провод. Подводящие
провода направлены вдоль линий магнитной
индукции.Квадратный контур со стороной
 см,
по которому течет ток
А, свободно установился в однородном
магнитном поле (B =10 мТл).
Определить изменение
см,
по которому течет ток
А, свободно установился в однородном
магнитном поле (B =10 мТл).
Определить изменение
 потенциальной энергии контура при
повороте вокруг оси, лежащей в плоскости
контура, на угол
потенциальной энергии контура при
повороте вокруг оси, лежащей в плоскости
контура, на угол
 .
.Тонкое проводящее кольцо с током
 А
помещено в однородное магнитное поле
(
А
помещено в однородное магнитное поле
( мТл). Плоскость кольца перпендикулярна
линиям магнитной индукции. Радиус R
кольца равен 20 см. Найти силу F,
растягивающую кольцо.
мТл). Плоскость кольца перпендикулярна
линиям магнитной индукции. Радиус R
кольца равен 20 см. Найти силу F,
растягивающую кольцо.Квадратная рамка из тонкого провода может свободно вращаться вокруг горизонтальной оси, совпадающей с одной из сторон. Масса рамки равна 20 г. Рамку поместили в однородное магнитное поле (
 Тл), направленное вертикально вверх.
Определить угол
,
на который отклонилась рамка от вертикали
когда по ней пропустили ток
Тл), направленное вертикально вверх.
Определить угол
,
на который отклонилась рамка от вертикали
когда по ней пропустили ток
 А.
А.По круговому витку радиусом
 см течет ток
см течет ток
 А. Виток расположен в однородном
магнитном поле (
А. Виток расположен в однородном
магнитном поле ( мТл) так, что нормаль к плоскости
контура составляет угол
мТл) так, что нормаль к плоскости
контура составляет угол
 с вектором
.
Определить изменение
потенциальной энергии контура при его
повороте на угол
с вектором
.
Определить изменение
потенциальной энергии контура при его
повороте на угол
 в направлении увеличения угла
в направлении увеличения угла
 .
.По тонкому кольцу радиусом см равномерно распределен заряд с линейной плотностью
 нКл/м. Кольцо вращается относительно
оси, перпендикулярной плоскости кольца
и проходящей через его центр, с частотой
нКл/м. Кольцо вращается относительно
оси, перпендикулярной плоскости кольца
и проходящей через его центр, с частотой
 с1.
Определить магнитный момент
с1.
Определить магнитный момент
 ,
обусловленный вращением кольца.
,
обусловленный вращением кольца.Диск радиусом
 см несет равномерно распределенный
по поверхности заряд (
см несет равномерно распределенный
по поверхности заряд ( нКл/м2). Определить магнитный
момент
,
обусловленный вращением диска,
относительно оси, проходящей через его
центр и перпендикулярной плоскости
диска. Угловая скорость вращения диска
нКл/м2). Определить магнитный
момент
,
обусловленный вращением диска,
относительно оси, проходящей через его
центр и перпендикулярной плоскости
диска. Угловая скорость вращения диска
 рад/с.
рад/с.Стержень длиной см заряжен равномерно распределенным зарядом с линейной плотностью
 мкКл/м. Стержень вращается с частотой
с1
относительно оси, перпендикулярной
стержню и проходящей через его конец.
Определить магнитный момент
,
обусловленный вращением стержня.
мкКл/м. Стержень вращается с частотой
с1
относительно оси, перпендикулярной
стержню и проходящей через его конец.
Определить магнитный момент
,
обусловленный вращением стержня.Протон движется по окружности радиусом
 см с линейной скоростью v = 106 м/с.
Определить магнитный момент
,
создаваемый эквивалентным круговым
током.
см с линейной скоростью v = 106 м/с.
Определить магнитный момент
,
создаваемый эквивалентным круговым
током.Тонкое кольцо радиусом см несет равномерно распределенный заряд
 нКл. Кольцо вращается с угловой
скоростью
нКл. Кольцо вращается с угловой
скоростью
 рад/с
относительно оси, совпадающей с одним
из диаметров кольца. Найти магнитный
момент
,
обусловленный вращением кольца.
рад/с
относительно оси, совпадающей с одним
из диаметров кольца. Найти магнитный
момент
,
обусловленный вращением кольца.Заряд
 мкКл равномерно распределен по
стержню длиной
мкКл равномерно распределен по
стержню длиной
 см.
Стержень вращается с угловой скоростью
см.
Стержень вращается с угловой скоростью
 рад/с
относительно оси, перпендикулярной
стержню и проходящей через его середину.
Найти магнитный момент
,
обусловленный вращением стержня.
рад/с
относительно оси, перпендикулярной
стержню и проходящей через его середину.
Найти магнитный момент
,
обусловленный вращением стержня.Сплошной цилиндр радиусом
 см и высотой
см и высотой
 см несет равномерно распределенный
по объему заряд (
см несет равномерно распределенный
по объему заряд ( мкКл/м3). Цилиндр вращается с
частотой
с1
относительно оси, совпадающей с его
геометрической осью. Найти магнитный
момент
цилиндра, обусловленный его вращением.
мкКл/м3). Цилиндр вращается с
частотой
с1
относительно оси, совпадающей с его
геометрической осью. Найти магнитный
момент
цилиндра, обусловленный его вращением.По тонкому стержню длиной
 см
равномерно распределен заряд
см
равномерно распределен заряд
 нКл.
Стержень вращается с частотой
нКл.
Стержень вращается с частотой
 с1
относительно оси, перпендикулярной
стержню и проходящей через стержень
на расстоянии
с1
относительно оси, перпендикулярной
стержню и проходящей через стержень
на расстоянии
 от одного из его концов. Определить
магнитный момент
,
обусловленный вращением, стержня.
от одного из его концов. Определить
магнитный момент
,
обусловленный вращением, стержня.Два иона разных масс с одинаковыми зарядами влетели в однородное магнитное поле, стали двигаться по окружностям радиусами
 см
и
см
и
 см. Определить отношение масс ионов,
если они прошли одинаковую ускоряющую
разность потенциалов.
см. Определить отношение масс ионов,
если они прошли одинаковую ускоряющую
разность потенциалов.Однозарядный ион натрия прошел ускоряющую разность потенциалов
 кВ и влетел перпендикулярно линиям
магнитной индукции в однородное поле
(
кВ и влетел перпендикулярно линиям
магнитной индукции в однородное поле
( Тл). Определить относительную
атомную массу А иона, если он описал
окружность радиусом
Тл). Определить относительную
атомную массу А иона, если он описал
окружность радиусом
 см.
см.Электрон прошел ускоряющую разность потенциалов
 В и, влетев в однородное магнитное
поле
В и, влетев в однородное магнитное
поле
 мТл, стал двигаться по винтовой
линии с шагом
мТл, стал двигаться по винтовой
линии с шагом
 мм. Определить радиус R
винтовой линии.
мм. Определить радиус R
винтовой линии.Альфа-частица прошла ускоряющую разность потенциалов
 В и, попав в однородное магнитное
поле, стала двигаться по винтовой линии
радиусом
В и, попав в однородное магнитное
поле, стала двигаться по винтовой линии
радиусом
 см и шагом
см и шагом
 см. Определить магнитную индукцию
В поля.
см. Определить магнитную индукцию
В поля.Заряженная частица прошла ускоряющую разность потенциалов
 В и, влетев в однородное магнитное
поле (
Тл),
стала двигаться по винтовой линии с
шагом
В и, влетев в однородное магнитное
поле (
Тл),
стала двигаться по винтовой линии с
шагом
 см и радиусом
см. Определить отношение заряда
частицы к ее массе.
см и радиусом
см. Определить отношение заряда
частицы к ее массе.Электрон влетел в однородное магнитное поле (
 мТл) перпендикулярно линиям магнитной
индукции. Определить силу эквивалентного
кругового тока
мТл) перпендикулярно линиям магнитной
индукции. Определить силу эквивалентного
кругового тока
 создаваемого движением электрона в
магнитном поле.
создаваемого движением электрона в
магнитном поле.Протон прошел ускоряющую разность потенциалов В и влетел в однородное магнитное поле (
 мТл) под углом
мТл) под углом
 к линиям магнитной индукции. Определить
шаг h и радиус R
винтовой линии, по которой будет
двигаться протон в магнитном поле.
к линиям магнитной индукции. Определить
шаг h и радиус R
винтовой линии, по которой будет
двигаться протон в магнитном поле.Альфа-частица, пройдя ускоряющую разность потенциалов U, стала двигаться в однородном магнитном поле (
 мТл) по винтовой линии с шагом
мТл) по винтовой линии с шагом
 см и радиусом
см.
Определить ускоряющую разность
потенциалов, которую прошла альфа-частица.
см и радиусом
см.
Определить ускоряющую разность
потенциалов, которую прошла альфа-частица.Ион с кинетической энергией
 КэВ попал в однородное магнитное
поле (
КэВ попал в однородное магнитное
поле ( мТл) и стал двигаться по окружности.
Определить магнитный момент
эквивалентного кругового тока.
мТл) и стал двигаться по окружности.
Определить магнитный момент
эквивалентного кругового тока.Ион, попав в магнитное поле (
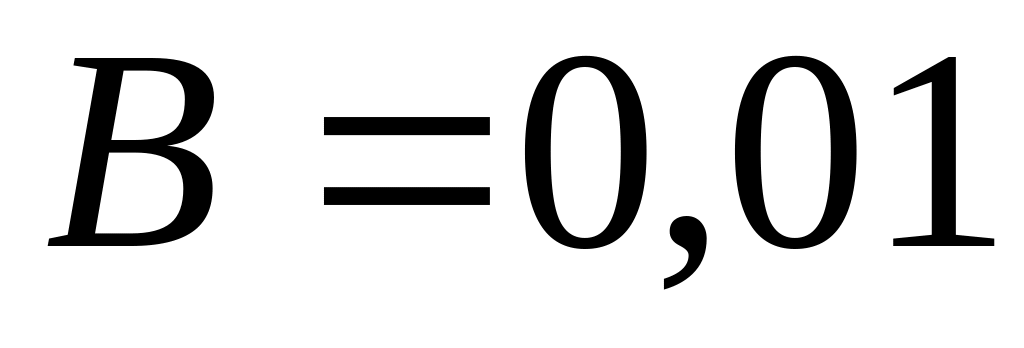 Тл), стал двигаться по окружности.
Определить кинетическую энергию Т
(в эВ) иона, если магнитный момент
эквивалентного кругового тока равен
1,6·1014
А·м2.
Тл), стал двигаться по окружности.
Определить кинетическую энергию Т
(в эВ) иона, если магнитный момент
эквивалентного кругового тока равен
1,6·1014
А·м2.Ион, пройдя ускоряющую разность потенциалов
 В, влетел в скрещенные под прямым
углом однородные магнитное (
В, влетел в скрещенные под прямым
углом однородные магнитное ( мТл) и электрическое (
мТл) и электрическое ( В/м) поля. Определить отношение
заряда иона к его массе, если ион в этих
полях движется прямолинейно.
В/м) поля. Определить отношение
заряда иона к его массе, если ион в этих
полях движется прямолинейно.Электрон, пройдя ускоряющую разность потенциалов
 кВ,
попал в скрещенные под прямым углом
однородные магнитное и электрическое
поля. Определить напряженность
электрического поля, если магнитная
индукция
поля равна 6 мТл.
кВ,
попал в скрещенные под прямым углом
однородные магнитное и электрическое
поля. Определить напряженность
электрического поля, если магнитная
индукция
поля равна 6 мТл.Однозарядный ион лития массой
 а.е.м. прошел ускоряющую разность
потенциалов
В
и влетел в скрещенные под прямым углом
однородные магнитное и электрическое
поля. Определить магнитную индукцию
поля, если траектория иона в скрещенных
полях прямолинейна. Напряженность
электрического поля равна 2 кВ/м.
а.е.м. прошел ускоряющую разность
потенциалов
В
и влетел в скрещенные под прямым углом
однородные магнитное и электрическое
поля. Определить магнитную индукцию
поля, если траектория иона в скрещенных
полях прямолинейна. Напряженность
электрического поля равна 2 кВ/м.Альфа-частица, имеющая скорость v = 2 Мм/с, влетает под углом к сонаправленному магнитному (
 мТл) и электрическому (
мТл) и электрическому ( кВ/м)
полям. Определить ускорение
альфа-частицы. (Ускорение определяется
в монет вхождения частицы в область
пространства, где локализованы однородные
магнитное и электрическое поля)
кВ/м)
полям. Определить ускорение
альфа-частицы. (Ускорение определяется
в монет вхождения частицы в область
пространства, где локализованы однородные
магнитное и электрическое поля)Протон прошел некоторую ускоряющую разность потенциалов U и влетел в скрещенные под прямым углом однородные поля: магнитное (
 мТл) и электрическое (
мТл) и электрическое ( кВ/м). Определить разность потенциалов
U, если протон в
скрещенных полях движется прямолинейно.
кВ/м). Определить разность потенциалов
U, если протон в
скрещенных полях движется прямолинейно.Плоский контур площадью
 см2 находится в однородном
магнитном поле (
см2 находится в однородном
магнитном поле ( Тл). Определить магнитный поток Ф,
пронизывающий контур, если плоскость
его составляет угол
Тл). Определить магнитный поток Ф,
пронизывающий контур, если плоскость
его составляет угол
 с направлением линий индукций.
с направлением линий индукций.Магнитный поток Ф сквозь сечение соленоида равен 50 мкВб. Длина соленоида см. Найти магнитный момент соленоида, если его витки плотно прилегают друг к другу.
В средней части соленоида, содержащего
 витков/см, помещен круговой виток
диаметром
витков/см, помещен круговой виток
диаметром
 см. Плоскость витка расположена
под углом
к оси соленоида. Определить магнитный
поток Ф, пронизывающий виток, если
по обмотке соленоида течет ток
см. Плоскость витка расположена
под углом
к оси соленоида. Определить магнитный
поток Ф, пронизывающий виток, если
по обмотке соленоида течет ток
 А.
А.На длинный картонный каркас диаметром
 см уложена однослойная обмотка
(виток к витку) из проволоки диаметром
см уложена однослойная обмотка
(виток к витку) из проволоки диаметром
 мм. Определить магнитный поток Ф,
создаваемый таким соленоидом при силе
тока
мм. Определить магнитный поток Ф,
создаваемый таким соленоидом при силе
тока
 А.
А.Квадратный контур со стороной см, в котором течет ток
 А,
находится в магнитном поле (
А,
находится в магнитном поле ( Тл) под углом
Тл) под углом
 к линиям индукции. Какую работу А
нужно совершить, чтобы при неизменной
силе тока в контуре изменить его форму
на окружность?
к линиям индукции. Какую работу А
нужно совершить, чтобы при неизменной
силе тока в контуре изменить его форму
на окружность?Плоский контур с током
 А
свободно установился в однородном
магнитном поле (
А
свободно установился в однородном
магнитном поле ( Тл). Площадь контура
Тл). Площадь контура
 см2. Поддерживая ток в контуре
неизменным, его повернули относительно
оси, лежащей в плоскости контура, на
угол
см2. Поддерживая ток в контуре
неизменным, его повернули относительно
оси, лежащей в плоскости контура, на
угол
 .
Определить совершенную при этом работу
А.
.
Определить совершенную при этом работу
А.Виток, в котором поддерживается постоянная сила тока А, свободно установился в однородном магнитном поле ( мТл). Диаметр витка см. Какую работу А нужно совершить для того, чтобы повернуть виток относительно оси, совпадающей с диаметром, на угол
 ?
?В однородном магнитном поле перпендикулярно линиям индукции расположен плоский контур площадью
 см2. Поддерживая в контуре
постоянную силу тока
А, его переместили из поля в область
пространства, где поле отсутствует.
Определить магнитную индукцию В
поля, если при перемещении контура была
совершена работа
см2. Поддерживая в контуре
постоянную силу тока
А, его переместили из поля в область
пространства, где поле отсутствует.
Определить магнитную индукцию В
поля, если при перемещении контура была
совершена работа
 Дж.
Дж.Плоский контур площадью с током А расположен в однородном магнитном поле (
 Тл) так, что нормаль к контуру
перпендикулярна линиям магнитной
индукции. Определить работу, совершаемую
силами поля при медленном повороте
контура около оси, лежащей в плоскости
контура, на угол
.
Площадь контура 2 см2.
Тл) так, что нормаль к контуру
перпендикулярна линиям магнитной
индукции. Определить работу, совершаемую
силами поля при медленном повороте
контура около оси, лежащей в плоскости
контура, на угол
.
Площадь контура 2 см2.Определить магнитный поток Ф, пронизывающий соленоид, если его длина см и магнитный момент
 Вб.
Вб.В однородном магнитном поле ( Тл) равномерно с частотой
 с1
вращается стержень длиной
см
так, что плоскость его вращения
перпендикулярна линиям напряженности,
а ось вращения проводит через один из
его концов. Определить индуцируемую
на концах стержня разность потенциалов
U.
с1
вращается стержень длиной
см
так, что плоскость его вращения
перпендикулярна линиям напряженности,
а ось вращения проводит через один из
его концов. Определить индуцируемую
на концах стержня разность потенциалов
U.В однородном магнитном поле с индукцией Тл вращается с частотой с1 стержень длиной см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определить разность потенциалов U на концах стержня.
В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. При этом по цепи прошел заряд
 мкКл. Определить изменение магнитного
потока
мкКл. Определить изменение магнитного
потока
 через кольцо, если сопротивление цепи
гальванометра
Ом.
через кольцо, если сопротивление цепи
гальванометра
Ом.Тонкий медный провод массой
 г согнут в виде квадрата, и концы
его замкнуты. Квадрат помещен в однородное
магнитное поле (
г согнут в виде квадрата, и концы
его замкнуты. Квадрат помещен в однородное
магнитное поле ( Тл) так, что его плоскость
перпендикулярна линиям поля. Определить
заряд Q, который
потечет по проводнику, если квадрат,
потянув за противоположные вершины,
вытянуть в линию.
Тл) так, что его плоскость
перпендикулярна линиям поля. Определить
заряд Q, который
потечет по проводнику, если квадрат,
потянув за противоположные вершины,
вытянуть в линию.Рамка из провода сопротивлением
 Ом равномерно вращается в однородном
магнитном поле (
Тл). Ось вращения лежит в плоскости
рамки и перпендикулярна линиям индукции.
Площадь рамки
см2. Определить заряд Q,
который потечет по рамке при изменении
угла между нормалью к рамке и линиями
индукции: 1) от 0 до 45°; 2) от 45 до 90°.
Ом равномерно вращается в однородном
магнитном поле (
Тл). Ось вращения лежит в плоскости
рамки и перпендикулярна линиям индукции.
Площадь рамки
см2. Определить заряд Q,
который потечет по рамке при изменении
угла между нормалью к рамке и линиями
индукции: 1) от 0 до 45°; 2) от 45 до 90°.Проволочный виток диаметром
 см
и сопротивлением
см
и сопротивлением
 Ом
находится в однородном магнит ном поле
(
Ом
находится в однородном магнит ном поле
( Тл). Плоскость витка составляет
угол
Тл). Плоскость витка составляет
угол
 с линиями индукции. Какой заряд Q
протечет по витку при выключении
магнитного поля?
с линиями индукции. Какой заряд Q
протечет по витку при выключении
магнитного поля?Рамка, содержащая
 витков тонкого провода, может свободно
вращаться относительно оси, лежащей в
плоскости рамки. Площадь рамки
витков тонкого провода, может свободно
вращаться относительно оси, лежащей в
плоскости рамки. Площадь рамки
 см2. Ось рамки перпендикулярна
линиям индукции однородного магнитного
поля (
см2. Ось рамки перпендикулярна
линиям индукции однородного магнитного
поля ( Тл). Определить максимальную ЭДС
Тл). Определить максимальную ЭДС
 ,
которая индуцируется в рамке при ее
вращении с частотой
,
которая индуцируется в рамке при ее
вращении с частотой
 с1
.
с1
.Прямой проводящий стержень длиной см находится в однородном магнитном поле ( Тл). Концы стержня замкнуты гибким проводом, находящимся вне поля. Сопротивление всей цепи Ом. Какая мощность Р потребуется для равномерного перемещения стержня перпендикулярно линиям магнитной индукции со скоростью v = 10 м/с?
Проволочный контур площадью
 см2 и сопротивлением
см2 и сопротивлением
 Ом
равномерно вращается в однородном
магнитном поле (
Тл).
Ось вращения лежит в плоскости кольца
и перпендикулярна линиям магнитной
индукции. Определить максимальную
мощность
Ом
равномерно вращается в однородном
магнитном поле (
Тл).
Ось вращения лежит в плоскости кольца
и перпендикулярна линиям магнитной
индукции. Определить максимальную
мощность
 ,
необходимую для вращения контура с
угловой скоростью
рад/с.
,
необходимую для вращения контура с
угловой скоростью
рад/с.Кольцо из медного провода массой
 г
помещено в однородное магнитное поле
(
г
помещено в однородное магнитное поле
( Тл) так, что плоскость кольца
составляет угол
Тл) так, что плоскость кольца
составляет угол
 60°
с линиями магнитной индукции. Определить
заряд Q, который
пройдет по кольцу, если снять магнитное
поле.
60°
с линиями магнитной индукции. Определить
заряд Q, который
пройдет по кольцу, если снять магнитное
поле.Соленоид сечением
 см2 содержит
см2 содержит
 витков. При силе тока
А магнитная индукция В поля
внутри соленоида равна 0,05 Тл.
Определить индуктивность L
соленоида.
витков. При силе тока
А магнитная индукция В поля
внутри соленоида равна 0,05 Тл.
Определить индуктивность L
соленоида.На картонный каркас длиной
 0,8
м и диаметром
0,8
м и диаметром
 см намотан в один слой провод
диаметром
см намотан в один слой провод
диаметром
 мм так, что витки плотно прилегают
друг к другу. Вычислить индуктивность
L получившегося
соленоида.
мм так, что витки плотно прилегают
друг к другу. Вычислить индуктивность
L получившегося
соленоида.Катушка, намотанная на магнитный цилиндрический каркас, имеет
 витков и индуктивность
витков и индуктивность
 мГн. Чтобы увеличить индуктивность
катушки до
мГн. Чтобы увеличить индуктивность
катушки до
 мГн, обмотку катушки сняли и заменили
обмоткой из более тонкой проволоки с
таким расчетом, чтобы длина катушки
осталась прежней. Сколько витков
оказалось в катушке после перемотки?
мГн, обмотку катушки сняли и заменили
обмоткой из более тонкой проволоки с
таким расчетом, чтобы длина катушки
осталась прежней. Сколько витков
оказалось в катушке после перемотки?Индуктивность L соленоида, намотанного в один слой на немагнитный каркас, равна 0,5 мГн. Длина
 соленоида равна 0,6 м, диаметр
соленоида равна 0,6 м, диаметр
 см.
Определить отношение
см.
Определить отношение
 числа витков соленоида к его длине.
числа витков соленоида к его длине.
Соленоид содержит
 витков. Сечение сердечника (из немагнитного
материала)
см2. По обмотке течет ток,
создающий поле с индукцией
витков. Сечение сердечника (из немагнитного
материала)
см2. По обмотке течет ток,
создающий поле с индукцией
 мТл. Определить среднее значение
ЭДС
мТл. Определить среднее значение
ЭДС
 самоиндукции, которая возникает на
зажимах соленоида, если сила тока
уменьшается практически до нуля за
время
самоиндукции, которая возникает на
зажимах соленоида, если сила тока
уменьшается практически до нуля за
время
 мс.
мс.По катушке индуктивностью
 мкГн течет ток
А. Определить среднее значение ЭДС
самоиндукции возникающей в контуре,
если сила тока изменится практически
до нуля за время
мкГн течет ток
А. Определить среднее значение ЭДС
самоиндукции возникающей в контуре,
если сила тока изменится практически
до нуля за время
 мс.
мс.В электрической цепи, содержащей резистор сопротивлением Ом и катушку индуктивностью
 Гн, течет ток
А. Определить силу тока
в цепи через
Гн, течет ток
А. Определить силу тока
в цепи через
 мс после ее размыкания.
мс после ее размыкания.Цепь состоит из катушки индуктивностью
 Гн и источника тока. Источник тока
отключили, не разрывая цепи. Время,
через которое сила тока уменьшится до
0,001 первоначального значения, равно
Гн и источника тока. Источник тока
отключили, не разрывая цепи. Время,
через которое сила тока уменьшится до
0,001 первоначального значения, равно
 с. Определить сопротивление катушки.
с. Определить сопротивление катушки.Источник тока замкнули на катушку сопротивлением Ом и индуктивностью
 Гн. Через какое время сила тока в
цепи постигнет 50% максимального значения?
Гн. Через какое время сила тока в
цепи постигнет 50% максимального значения?Источник тока замкнули на катушку сопротивлением Ом. Через время
 с
сила тока
в катушке достигла 0,95 предельного
значения. Определить индуктивность L
катушки.
с
сила тока
в катушке достигла 0,95 предельного
значения. Определить индуктивность L
катушки.
Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус r3 третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны =0,6 мкм равен 0,82 мм. Радиус кривизны линзы R=0,5 м.
На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны
 =500
нм. Отраженный от нее свет максимально
усилен вследствие интерференции.
Определить минимальную толщину dmin
пленки, если показатель преломления
материала пленки п=1,4.
=500
нм. Отраженный от нее свет максимально
усилен вследствие интерференции.
Определить минимальную толщину dmin
пленки, если показатель преломления
материала пленки п=1,4.Расстояние L от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной l=1 см укладывается N=10 темных интерференционных полос. Длина волны =0,7 мкм.
На стеклянную пластину положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны =500 нм. Найти радиус R линзы, если радиус четвертого, темного кольца Ньютона в отраженном свете r4=2 мм.
На тонкую глицериновую пленку толщиной d = 1,5 мкм нормально к ее поверхности падает белый свет. Определить длины волн лучей участка спектра (0,4

0,8
мкм), которые будут ослаблены в
результате интерференции.
0,8
мкм), которые будут ослаблены в
результате интерференции.На стеклянную пластину нанесен тонкий слой прозрачного вещества с показателем преломления п=1,3. Пластинка освещена параллельным пучком монохроматического света с длиной волны =640 нм, падающим на пластинку нормально. Какую минимальную толщину dmin должен иметь слой, чтобы отраженный пучок имел наименьшую яркость?
На тонкий стеклянный клин падает нормально параллельный пучок света с длиной волны =500 нм. Расстояние между соседними темными интерференционными полосами в отраженном свете b=0,5 мм. Определить угол между поверхностями клина. Показатель преломления стекла, из которого изготовлен клин, п=1,6.
Плосковыпуклая стеклянная линза с f=1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете r5=1,1 мм. Определить длину световой волны .
Между двумя плоскопараллельными пластинами на расстоянии L=10 см от границы их соприкосновения находится проволока диаметром d=0,01 мм, образуя воздушный клин. Пластины освещают нормально падающим монохроматическим светом (=0,6 мкм). Определить ширину b интерференционных полос, наблюдаемых в отраженном свете.
Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом ( = 590 нм). Радиус кривизны R линзы равен 5 см. Определить толщину d3 воздушного промежутка в том месте, где в отраженном свете наблюдается третье световое кольцо.
На пути пучка света поставлена стеклянная пластина толщиной d = 1 мм так, что угол падения луча i1 =30. На сколько изменится оптическая длина пути светового пучка?
На мыльную пленку с показателем преломления n = 1,33 падает по нормали монохроматический свет с длиной волны =0,6 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова наименьшая возможная толщина dmin пленки?
Радиус второго темного кольца Ньютона в отраженном свете r2 = 0,4 мм. Определить радиус R кривизны плосковыпуклой линзы, взятой для опыты, если она освещается монохроматическим светом с длиной волны = 0,05 мкм.
На тонкую пленку с показателем преломления n = 1,33 под углом i1 =52 падает параллельный пучок белого света. При какой толщине пленки отраженный свет будет наиболее сильно окрашен в желтый цвет ( = 600 нм)? Считать, что световой вектор перпендикулярен к плоскости падения.
Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр ( = 500 нм) заменить красным ( = 650 нм)?
Какое наименьшее число Nmin штрихов должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн 1 = 589 нм и 2 = 589,6 нм? Какова длина l такой решетки, если ее постоянная d = 5 мкм?
На поверхность дифракционной решетки нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в п=4,6 раза больше длины световой волны. Найти общее число М дифракционных максимумов, которые теоретически можно наблюдать в данном случае.
На дифракционную решетку падает нормально параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница ( = 780 нм) спектра третьего порядка?
На дифракционную решетку, содержащую п = 600 штрихов на миллиметр, падает нормально белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана L = 1,2 м. Границы видимого спектра: кр = 780 нм, ф = 400 нм.
На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние d между атомными плоскостями равно 280 пм. Под углом = 65 к атомной плоскости наблюдается дифракционный максимум первого порядка. Определить длину волны рентгеновского излучения.
На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна ( = 600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, = 20˚. Определить ширину a щели.
На дифракционную решетку, содержащую п=100 штрихов на 1 мм, нормально падает монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол = 16. Определить длину волны света, падающего на решетку.
На дифракционную решетку падает нормально монохроматический свет ( = 410 нм). Угол между направлениями на максимумы первого и второго порядков равен 221'. Определить число п штрихов на 1 мм дифракционной решетки.
Постоянная дифракционной решетки в п=4 раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол между двумя первыми симметричными дифракционными максимумами.
Расстояние между штрихами дифракционной решетки d=4 мкм. На решетку падает нормально свет с длиной волны = 0,58 мкм. Максимум какого наибольшего порядка дает эта решетка?
Свет от монохроматического источника ( = 600 нм) падает нормально на диафрагму с диаметром отверстия d = 6 мм. За диафрагмой на расстоянии l = 3 м от нее находится экран. Какое число k зон Френеля укладывается в отверстие диафрагмы?
Дифракционная картина наблюдается на расстоянии l от точечного источника монохроматического света ( = 600 нм). На расстоянии a = 0,5l от источника помещена круглая непрозрачная преграда диаметром d = 1 см. Найти расстояние l, если преграда закрывает только центральную зону Френеля.
Между точечным источником света ( = 0,50 мкм) и экраном поместили диафрагму с круглым отверстием r = 1 мм. Расстояния от диафрагмы до источника и экрана равны соответственно R = 1 м и r0 = 2 м. Как изменится освещенность экрана в точке, лежащей против центра отверстия, если диафрагму убрать?
Между точечным источником света ( = 0,50 мкм) и экраном поместили диафрагму с круглым отверстием r1 = 0,75 мм. Расстояния от диафрагмы до источника и экрана равны соответственно R = r0 = 0,75 м. Как изменится освещенность экрана в точке, лежащей против центра отверстия, если его радиус увеличить до r2 = 0,87 мм?
На щель падает нормально параллельный пучок монохроматического света. Расположенная за щелью линза с фокусным расстоянием f = 2 м. проектирует на экран дифракционную картину в виде чередующихся светлых и темных полос. Ширина центральной светлой полосы b = 5 см. Как надо изменить ширину щели, чтобы центральная полоса занимала весь экран при любой ширине последнего?
Пластинку кварца толщиной d = 2 мм поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол = 53. Какой наименьшей толщины dmin следует взять пластинку, чтобы поле зрения поляриметра стало совершенно темным?
Параллельный пучок света переходит из глицерина в стекло так, что пучок, отраженный от границы раздела этих сред, оказывается максимально поляризованным. Определить угол между падающим и преломленным пучками.
Кварцевую пластинку поместили между скрещенными николями. При какой наименьшей толщине dmin кварцевой пластины поле зрения между николями будет максимально просветлено? Постоянная вращения кварца равна 27 град/мм.
При прохождении света через трубку длиной l1=20 см, содержащую раствор сахара концентрацией С1=10%, плоскость поляризации света повернулась на угол 1 = 13,3. В другом растворе сахара, налитом в трубку длиной l2=15 см, плоскость поляризации повернулась на угол 2 = 5,2. Определить концентрацию С2 второго раствора.
Пучок света последовательно проходит через два николя, плоскости пропускания которых образуют между собой угол = 40. Принимая, что коэффициент поглощения k каждого николя равен 0,15, найти, во сколько раз пучок света, выходящий из второго николя, ослаблен по сравнению с пучком, падающим на первый николь.
Угол падения луча на поверхность стекла равен 60. При этом отраженный пучок света оказался максимально поляризованным. Определить угол
 преломления луча.
преломления луча.Угол между плоскостями пропускания поляроидов равен 50. Естественный свет, проходя через такую систему, ослабляется в п=8 раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения k света в поляроидах.
Пучок света, идущий в стеклянном сосуде с глицерином, отражается от дна сосуда. При каком угле падения отраженный пучок света максимально поляризован?
Пучок света переходит из жидкости в стекло. Угол падения пучка равен 60˚, угол преломления
 = 50.
При каком угле падения
= 50.
При каком угле падения
 пучок света, отраженный от границы
раздела этих сред, будет максимально
поляризован?
пучок света, отраженный от границы
раздела этих сред, будет максимально
поляризован?Пучок света падает на плоскопараллельную стеклянную пластину, нижняя поверхность которой находится в воде. При каком угле падения свет, отраженный от границы – вода, будет максимально поляризован?
На сколько процентов уменьшится интенсивность света после прохождения через призму Николя, если потери света составляют 10%?
Естественный свет проходит через поляризатор и анализатор, поставленный так, что угол между их главными плоскостями равен . Как поляризатор, так и анализатор поглощают и отражают 8% падающего на них света. Оказалось, что интенсивность луча, вышедшего из анализатора, равна 9% интенсивности естественного света, падающего на поляризатор. Найти угол .
Луч света проходит через жидкость, налитую в стеклянный (n = 1,5) сосуд и отражается от дна. Отраженный луч полностью поляризован при падении его на дно сосуда под углом iб = 4237'. Найти показатель преломления жидкости. Под каким углом i должен падать на дно сосуда луч света, идущий в этой жидкости, чтобы наступило полное внутреннее отражение?
Угол полной поляризации при отражении от кристалла каменной соли = 5705'. Определить скорость v распространения света в этом кристалле.
Найти угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через поляризатор и анализатор, уменьшается в 4 раза.
Вычислить истинную температуру Т вольфрамовой раскаленной ленты, если радиационный периметр показывает температуру Трад=2,5 кК. Принять, что поглощательная способность для вольфрама не зависит от частоты излучения и равна аi=0,35.
Черное тело имеет температуру Т1=500 К. Какова будет температура Т2 тела, если в результате нагревания поток излучения увеличится в п=5 раз?
Температура абсолютно черного тела Т=2 кК. Определить длину волны
 ,
на которую приходится максимум
энергии излучения, и спектральную
плотность энергетической светимости
(r,T)max
для этой длины волны.
,
на которую приходится максимум
энергии излучения, и спектральную
плотность энергетической светимости
(r,T)max
для этой длины волны.Определить температуру Т и энергетическую светимость Re абсолютно черного тела, если максимум энергии излучения приходится на длину волны m = 600 нм.
Из смотрового окошечка печи излучается поток Фе = 4 кДж/мин. Определить температуру Т печи, если площадь окошечка S=8 см2.
Поток излучения абсолютно черного тела Фе = 10 кВт. Максимум энергии излучения приходится на длину волны m = 0,8 мкм. Определить площадь излучающей поверхности.
Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (m1 = 780 нм) на фиолетовую (m2 = 390 нм)?
Определить поглощательную способность aТ серого тела, для которого температура, измеренная радиационным пирометром, Трад=1,4 кК, тогда как истинная температура Т тела равна 3,2 кК.
Муфельная печь, потребляющая мощность, P=1 кВт, имеет отверстие площадью S=100 см2. Определить долю мощности, рассеиваемой стенками печи, если температура ее внутренней поверхности равна 1 кК.
Средняя энергетическая светимость R поверхности Земли равна 0,54 Дж/(см2мин). Какова должна быть температура Т поверхности Земли, если условно считать, что она излучает как серое тело с коэффициентом черноты aТ=0,25?
Вычислить энергию, излучаемую за время t = 1 мин с площади S = 1 см2 абсолютно черного тела, температура которого T = 1000 K.
Электрическая печь потребляет мощность P = 500 Вт. Температура ее внутренней поверхности при открытом небольшом отверстии диаметром d = 5 см равна 700C. Какая часть потребляемой мощности рассеивается стенками?
Мощность излучения абсолютно черного тела P = 10 кВт. Найти площадь S излучающей поверхности тела, если максимум спектральной плотности его энергетической светимости приходится на длину волны = 700 нм.
Абсолютно черное тело имеет температуру T1 = 2900 K. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на = 9 мкм. До какой температуры T2 охладилось тело?
Поверхность тела нагрета до температуры T = 1000 K. Затем одна половина этой поверхности нагревается на T = 100 K, а другая охлаждается на T = 100 K. Во сколько раз изменится энергетическая светимость R поверхности тела?
Красная граница фотоэффекта для цинка 0 = 310 нм. Определить максимальную кинетическую энергию Ek,max фотоэлектронов в электрон-вольтах, если на цинк падает свет с длиной волны = 200 нм.
На поверхность калия падает свет с длиной волны = 150 нм. Определить максимальную кинетическую энергию Ek,max фотоэлектронов.
Фотон с энергией = 10 эВ падает на серебряную пластину и вызывает фотоэффект. Определить импульс р, полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластин.
На фотоэлемент с катодом из лития падает свет с длиной волны = 200 нм. Найти наименьшее значение задерживающей разности потенциалов Umin, которую нужно приложить к фотоэлементу, чтобы прекратить фототок.
Какова должна быть длина волны -излучения, падающего на платиновую пластину, чтобы максимальная скорость фотоэлектронов была vmax = 3 Мм/с?
На металлическую пластину направлен пучок ультрафиолетового излучения ( = 0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов Umin=0,96 В. Определить работу выхода А электронов из металла.
На поверхность металла падает монохроматический свет с длиной волны = 0,1 мкм. Красная граница фотоэффекта 0 = 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
На металл падает рентгеновское излучение с длиной волны = 1 нм. Пренебрегая работой выхода, определить максимальную скорость vmax фотоэлектронов.
На металлическую пластину направлен монохроматический пучок света с частотой = 7,31014 Гц. Красная граница 0 фотоэффекта для данного материала равна 560 нм. Определить максимальную скорость vmax фотоэлектронов.
На цинковую пластину направлен монохроматический пучок света. Фототок прекращается при задерживающей разности потенциалов U=1,5 В. Определить длину волны света, падающего на пластину.
На металлическую пластину падает монохроматический свет ( = 0, 413 мкм). Поток фотоэлектронов, вырываемых с поверхности металла, полностью задерживается, когда разность потенциалов тормозящего электрического поля достигает U=1 В. Определить работу выхода в электронвольтах и красную границу фотоэффекта.
Фотоны с энергией = 4,9 эВ вырывают электроны из металла с работой выхода A = 4,5 эВ. Найти максимальный импульс, передаваемый поверхности металла при вылете каждого электрона.
Найти постоянную Планка h, если известно, что электроны, вырываемые из металла светом с частотой 1 = 2,21015 Гц, полностью задерживаются разностью потенциалов U1 =6,6 В, а вырываемые светом с частотой 2 = 4,61015 Гц - разностью потенциалов U2 =16,5 В.
Определить максимальную скорость vmax фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучение с длиной волны 1 = 0,155 мкм; 2) -излучением с длиной волны 2 = 1 пм.
На пластину падает монохроматический свет ( = 0,42 мкм). Фототок прекращается при задерживающей разности потенциалов U2 = 0,95 В. Определить работу выхода A электронов с поверхности пластины.
Фотон при эффекте Комптона на свободном электроне был рассеян на угол =/2. Определить импульс р (в МэВ/с), приобретенный электроном, если энергия фотона до рассеивания была 1 = 1,02 МэВ.
Рентгеновское излучение ( = 1 нм) рассеивается электронами, которые можно считать практически свободными. Определить максимальную длину волны max рентгеновского излучения в рассеянном пучке.
Какая доля энергии фотона приходится при эффекте Комптона на электрон отдачи, если рассеяние фотона происходит на угол
 =/2?
Энергия фотона до рассеяния 1 = 0,51
МэВ.
=/2?
Энергия фотона до рассеяния 1 = 0,51
МэВ.Определить максимальное изменение длины волны ()max при комптоновском рассеянии свет на свободных электронах и свободных протонах.
Фотон с длиной волны 1 = 15 пм рассеялся на свободном электроне. Длина волны рассеянного фотона 2 = 16 пм. Определить угол рассеяния.
Фотон с энергией 1 = 0,51 МэВ был рассеян при эффекте Комптона на свободном электроне на угол =180. Определить кинетическую энергию Т электрона отдачи.
В результате эффекта Комптона фотон с энергией рассеян на свободных электронах на угол =150. Определить энергию 2 рассеянного фотона.
Определить угол , на который был рассеян квант с энергией 1 = 1,53 МэВ при эффекте Комптона, если кинетическая энергия электрона отдачи Т=0,51 МэВ.
Фотон с энергией 1 = 0,51 МэВ при рассеянии на свободном электроне потерял половину своей энергии. Определить угол рассеяния .
Определить импульс ре электрона отдачи, если фотон с энергией 1 = 1,53 МэВ в результате рассеяния на свободном электроне потерял 1/3 своей энергии.
Определить энергетическую освещенность (облученность) Ее зеркальной поверхности, если давление р, производимое излучением равно 40 мкПа. Излучение падает нормально к поверхности.
Давление р света с длиной волны = 40 нм, падающего нормально на черную поверхность, равно 2 нПа. Определить число N фотонов, падающих за время t = 10 c на площадь S = 1 мм2 этой поверхности.
Определить коэффициент отражения поверхности, если при энергетической освещенности Ее=120 Вт/м2 давление р света на нее оказалось равным 0,5 мкПа.
На расстоянии r = 5 м от точечного монохроматического ( = 0,5 мкм) изотропного источника расположена площадка (S=8 мм2) перпендикулярно падающим пучкам. Определить число N фотонов, ежесекундно падающих на площадку. Мощность излучения Р=100 Вт.
Точечный источник монохроматического ( = 1 нм) излучения находится в центре сферической зачерненной колбы радиусом R=10 см. Определить световое давление р, производимое на внутреннюю поверхность колбы, если мощность источника Р=1 кВт.
Невозбужденный атом водорода поглощает квант излучения с длиной волны = 102,6 нм. Вычислить, пользуясь теорией Бора, радиус
 электронной орбиты возбужденного
атома водорода.
электронной орбиты возбужденного
атома водорода.Вычислить по теории Бора радиус
 второй стационарной орбиты и скорость
v2 электрона
на этой орбите для атома водорода.
второй стационарной орбиты и скорость
v2 электрона
на этой орбите для атома водорода.Вычислить по теории Бора период Т вращения электрона в атоме водорода, находящегося в возбужденном состоянии, определяемом главным квантовым числом
 .
.Определить изменение энергии
 электрона в атоме водорода при излучении
атомом фотона с частотой
электрона в атоме водорода при излучении
атомом фотона с частотой
 Гц.
Гц.Во сколько раз изменится период Т вращения электрона в атоме водорода, если при переходе в невозбужденное состояние атом излучил фотон с длиной волны
 нм?
нм?На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны
 нм?
нм?В каких пределах должна лежать длина волн монохроматического света, чтобы при возбуждении атомов водорода квантами этого света радиус
 орбиты электрона увеличился в 16 раз?
орбиты электрона увеличился в 16 раз?В однозарядном ионе лития электрон перешел с четвертого энергетического уровня на второй. Определить длину волны излучения, испущенного ионом лития.
Электрон в атоме водорода находится на третьем энергетическом уровне. Определить кинетическую Ek, потенциальную Ep и полную Е энергию электрона. Ответ выразить в электрон-вольтах.
Фотон выбивает из атома водорода, находящегося в основном состоянии, электрон с кинетической энергией Ek = 10 эВ. Определить энергию
 фотона.
фотона.Определить квантовое число n возбужденного состояния атома водорода, если известно, что при переходе в основное состояние атом излучил: 1) фотон с длиной волны = 97,25 нм; 2) два фотона, с 1 = 656,3 нм и 2 = 121,6 нм.
Определить скорость, которую приобрел покоившейся атом водорода в результате излучения фотона при переходе из первого возбужденного состояния в основное.
Вычислить радиус первой боровской орбиты однократно ионизированного атома гелия.
Максимальная длина волны спектральной водородной линии серии Лаймана равна 0,12 мкм. Предполагая, что постоянная Ридберга неизвестна, определить максимальную длину волны линии серии Бальмера.
Определить изменение орбитального механического момента электрона при переходе его из возбужденного состояния в основное с испусканием фотона длиной волны = 1,0210–7 м.
Вычислить наиболее вероятную дебройлевскую длину волны
 молекул азота, содержащихся в воздухе
при комнатной температуре.
молекул азота, содержащихся в воздухе
при комнатной температуре.Определить энергию E, которую необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от
 нм
до
нм
до
 нм.
нм.На сколько по отношению к комнатной должна измениться температура идеального газа, чтобы дебройлевская, длина волны его молекул уменьшилась на 20%?
Параллельный пучок моноэнергетических электронов падает нормально на диафрагму в виде узкой прямоугольной щели, ширина которой a = 0,06 мм. Определить скорость этих электронов, если известно, что на экране, отстоящем от щели на расстоянии мм, ширина центрального дифракционного максимума
 мкм.
мкм.При каких значениях кинетической энергии Ek электрона ошибка в определении дебройлевской длины волны по нерелятивистской формуле не превышает 10%?
Из катодной трубки на диафрагму с узкой прямоугольной щелью нормально к плоскости диафрагмы направлен поток моноэнергетических электронов. Определить анодное напряжение трубки, если известно, что на экране, отстоящем от щели на расстоянии
 м, ширина центрального дифракционного
максимума
м, ширина центрального дифракционного
максимума
 мкм. Ширину b щели
принять равной 0,10 мм.
мкм. Ширину b щели
принять равной 0,10 мм.Протон обладает кинетической энергией E = 1 кэВ. Определить дополнительную энергию E которую необходимо ему сообщить для того, чтобы длина волны де Бройля уменьшилась в три раза.
Определить длины волн де Бройля -частйцы и протона, прошедших одинаковую ускоряющую разность потенциалов кВ.
Электрон обладает кинетической энергией E = 1 ,02 МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия E электрона уменьшится вдвое?
Кинетическая энергия E электрона равна удвоенному значению его энергии покоя (
 ).
Вычислить длину волны
де Бройля для такого электрона.
).
Вычислить длину волны
де Бройля для такого электрона.Вычислить длину волны де Бройля для протона, движущегося со скоростью v = 0,6c.
Найти кинетическую энергию, при которой дебройлевская длина волны электрона равна его комптоновской длине волны.
Определить длину волны де Бройля для атома водорода, движущегося при температуре T = 293 K с наиболее вероятной скоростью.
Определить длину волны де Бройля для нейтрона, движущегося при температуре T = 290 K со средней квадратичной скоростью.
Протон движется в однородном магнитном поле с индукцией B =15 мТл по окружности радиусом R = 1,4 м. Определить длину волн де Бройля для протона.
Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм.
Используя соотношение неопределенностей, оценить наименьшие ошибки v в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью 1 мкм.
Какова должна быть кинетическая энергия E протона в моноэнергетическом пучке, используемого для исследования структуры с линейными размерами
 см?
см?Используя соотношение неопределенностей, оценить ширину l одномерного потенциального ящика, в котором минимальная энергия электрона
 эВ.
эВ.Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину l ящика, если известно, что минимальная энергия -частицы
 МэВ.
МэВ.Среднее время жизни атома в возбужденном состоянии составляет
 с.
При переходе атома в нормальное
состояние испускается фотон, средняя
длина волны <>
которого равна 600 нм. Оценить
ширину ,
излучаемой спектральной линии, если
не происходит ее уширения за счет
других процессов.
с.
При переходе атома в нормальное
состояние испускается фотон, средняя
длина волны <>
которого равна 600 нм. Оценить
ширину ,
излучаемой спектральной линии, если
не происходит ее уширения за счет
других процессов.Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределенность
 радиуса
электронной орбиты и неопределенность
радиуса
электронной орбиты и неопределенность
 импульса р электрона на такой
орбите соответственно связаны следующим
образом:
импульса р электрона на такой
орбите соответственно связаны следующим
образом:
 и
и
 .
Используя эти связи, а также соотношение
неопределенностей, найти значение
радиуса электронной орбиты,
соответствующего минимальной энергии
электрона в атоме водорода.
.
Используя эти связи, а также соотношение
неопределенностей, найти значение
радиуса электронной орбиты,
соответствующего минимальной энергии
электрона в атоме водорода.Моноэнергетический пучок электронов высвечивает в центре экрана электронно-лучевой трубки пятно радиусом
 см. Пользуясь соотношением
неопределенностей, найти, во сколько
раз неопределенность
см. Пользуясь соотношением
неопределенностей, найти, во сколько
раз неопределенность
 координаты электрона на экране в
направлении, перпендикулярном оси
трубки, меньше размера r
пятна. Длину L
электронно-лучевой трубки принять
равной 0,50 м, а ускоряющее электрон
напряжение U
равным 20 кВ.
координаты электрона на экране в
направлении, перпендикулярном оси
трубки, меньше размера r
пятна. Длину L
электронно-лучевой трубки принять
равной 0,50 м, а ускоряющее электрон
напряжение U
равным 20 кВ.Среднее время жизни t атома в возбужденном состоянии составляет около
 с.
При переходе атома в нормальное
состояние испускается фотон, средняя
длина волны <>
которого равна 400 нм. Оценить
относительную ширину
с.
При переходе атома в нормальное
состояние испускается фотон, средняя
длина волны <>
которого равна 400 нм. Оценить
относительную ширину
 излучаемой спектральной линии, если
не происходит уширения линии за счет
других процессов.
излучаемой спектральной линии, если
не происходит уширения линии за счет
других процессов.Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределенность радиуса электронной орбиты и неопределенность импульса р электрона на такой орбите соответственно связаны следующим образом: и . Используя эти связи, а также соотношение неопределенностей, определить минимальное значение энергии Emin электрона в атоме водорода.
Определить относительную неопределенность
 импульса движущейся частицы, если
допустить, что неопределенность ее
координаты равна длине волны де Бройля.
импульса движущейся частицы, если
допустить, что неопределенность ее
координаты равна длине волны де Бройля.Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10% от ее числового значения, определить неопределенность координаты электрона.
Электронный пучок выходит из электронной пушки под действием разности потенциалов U = 200 В. Определить, можно ли одновременно измерить траекторию электрона с точностью до 100 пм и его скорость с точностью до 10%.
Определить отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10–5 м, и пылинки массой 10–12 кг, если ее координата установлена с такой же точностью.
Ширина следа электрона (обладающего кинетической энергией 1,5 эВ) на фотопластинке, полученного с помощью камеры Вильсона, составляет 1 мкм. Определить, можно ли по данному следу обнаружить отклонение в движении электрона от законов классической механики.
Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Найти отношение разности
 соседних энергетических уровней к
энергии
соседних энергетических уровней к
энергии
 частицы в трех случаях: 1)
;
2)
;
3)
частицы в трех случаях: 1)
;
2)
;
3)
 .
.Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l = 0,1 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.
Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l находится в возбужденном состоянии (
 ).
Определить, в каких точках интервала
).
Определить, в каких точках интервала
 плотность вероятности нахождения
частицы имеет максимальное и минимальное
значения.
плотность вероятности нахождения
частицы имеет максимальное и минимальное
значения.В прямоугольной потенциальной яме шириной l с абсолютно непроницаемыми стенками ( ) находится частица в основном состоянии. Найти вероятность местонахождения этой частицы в области
 .
.Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения частицы в крайней четверти ящика?
Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид
 ,
где А – некоторая постоянная;
,
где А – некоторая постоянная;
 – первый боровский радиус. Найти
для основного состояния атома водорода
наиболее вероятное расстояние электрона
от ядра.
– первый боровский радиус. Найти
для основного состояния атома водорода
наиболее вероятное расстояние электрона
от ядра.Частица находится в основном состоянии в прямоугольной яме шириной l с абсолютно непроницаемыми стенками. Во сколько раз отличаются вероятности местонахождения частицы:
 - в крайней трети и
- в крайней трети и
 - в крайней четверти ящика?
- в крайней четверти ящика?Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид , где А – некоторая постоянная; - первый боровский радиус. Найти для основного состояния атома водорода среднее значение
 кулоновской силы.
кулоновской силы.Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l. В каких точках в интервале плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы? Вычислить плотность вероятности для этих точек. Решение пояснить графиком.
Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид , где А – некоторая постоянная; - первый боровский радиус. Найти для основного состояния атома водорода среднее значение <П> потенциальной энергии.
Электрон находится в прямоугольном потенциальном ящике с непроницаемыми стенками. Ширина ящика l = 0,2 нм, энергия электрона в ящике E = 37,8 эВ. Определить n номер энергетического уровня.
Частица в одномерном прямоугольном потенциальном ящике шириной l с бесконечно высокими стенками находится в возбужденном состоянии (n =3)/ Определить, в каких точках ящика (0 x l) плотность вероятности обнаружения частицы максимальна. Поясните графически.
Частица в одномерном прямоугольном потенциальном ящике шириной l с бесконечно высокими стенками находится в возбужденном состоянии (n =3)/ Определить, в каких точках ящика (0 x l) плотность вероятности обнаружения частицы минимальна. Поясните графически.
Математический маятник можно рассматривать в качестве гармонического осциллятора. Определите в электрон-вольтах энергию нулевых колебаний для маятника длиной l = 1 м, находящегося в поле тяготения Земли.
Частица в потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения частицы в средней трети ящика?
Найти период полураспада
 радиоактивного изотопа, если его
активность за время
радиоактивного изотопа, если его
активность за время
 сут уменьшилась на 24% по сравнению
с первоначальной.
сут уменьшилась на 24% по сравнению
с первоначальной.Определить, какая доля радиоактивного изотопа
 распадается в течение времени t
= 6 сут.
распадается в течение времени t
= 6 сут.Активность А некоторого изотопа за время t = 10 сут уменьшилась на 20%. Определить период полураспада этого изотопа.
Определить массу m изотопа
 ,
имеющего активность А = 37 ГБк.
,
имеющего активность А = 37 ГБк.Найти среднюю продолжительность жизни
 атома радиоактивного изотопа кобальта
атома радиоактивного изотопа кобальта
 .
.Счетчик -частиц, установленный вблизи радиоактивного изотопа, при первом измерении регистрировал N1 = 1400 частиц в минуту, а через время t = 4 ч только N2 = 400. Определить период полураспада изотопа.
Во сколько раз уменьшится активность изотопа
 через время t = 20 сут?
через время t = 20 сут?На сколько процентов уменьшится активность изотопа иридия
 за время
за время
 сут?
сут?Определить число N ядер, распадающихся в течение времени: 1)
 мин; 2)
мин; 2)
 сут,
- в радиоактивном изотопе фосфора
массой
сут,
- в радиоактивном изотопе фосфора
массой
 мг.
мг.Из каждого миллиона атомов радиоактивного изотопа каждую секунду распадается 200 атомов. Определить период полураспада изотопа.
Изотоп радия с массовым числом 226 превратился в изотоп свинца с массовым числом 206. сколько - и -распадов произошло при этом?
Может ли ядро кремния превратиться в ядро фосфора? Какие частицы должны при этом выделиться? Какова их суммарная энергия?
Активность препарата урана с массовым числом 238 равна 2,5104 расп/с, масса препарата 2 г. Найти период полураспада.
Определить во сколько раз начальное количество ядер радиоактивного изотопа уменьшится за три года, если за один год оно уменьшилось в 4 раза.
Активность некоторого радиоактивного изотопа в начальный момент времени составляла 100 Бк. Определите активность этого изотопа по истечении промежутка времени, равного половине периода полураспада.
Определить количество теплоты Q, выделяющейся при распаде радона активностью
 Бк за время t =
20 мин. Кинетическая энергия Т
вылетающей из радона
-частицы
равна 5,5 МэВ.
Бк за время t =
20 мин. Кинетическая энергия Т
вылетающей из радона
-частицы
равна 5,5 МэВ.Масса г урана
 в равновесии с продуктами его распада
выделяет мощность
в равновесии с продуктами его распада
выделяет мощность
 Вт. Найти молярную теплоту
Вт. Найти молярную теплоту
 ,
выделяемую ураном за среднее время
жизни
атомов урана.
,
выделяемую ураном за среднее время
жизни
атомов урана.Определить энергию, необходимую для разделения ядра
 на две
-частицы
и ядро
на две
-частицы
и ядро
 .
Энергии связи на один нуклон в ядрах
20Ne, 4He
и 12С равны соответственно 8,03;
7,07 и 7,68 МэВ.
.
Энергии связи на один нуклон в ядрах
20Ne, 4He
и 12С равны соответственно 8,03;
7,07 и 7,68 МэВ.В одном акте деления ядра урана
 освобождается энергия 200 МэВ.
Определить: 1) энергию, выделяющуюся
при распаде всех ядер этого изотопа
урана массой
кг; 2) массу каменного угля с удельной
теплотой сгорания q
= 29,3 МДж/кг, эквивалентную в
тепловом отношении 1 кг урана
.
освобождается энергия 200 МэВ.
Определить: 1) энергию, выделяющуюся
при распаде всех ядер этого изотопа
урана массой
кг; 2) массу каменного угля с удельной
теплотой сгорания q
= 29,3 МДж/кг, эквивалентную в
тепловом отношении 1 кг урана
.Мощность Р двигателя атомного судна составляет 15 МВт, его КПД равен 30%. Определить месячный расход ядерного горючего при работе этого двигателя.
Считая, что в одном акте деления ядра урана освобождается энергия 200 МэВ, определить массу т этого изотопа, подвергшегося делению при взрыве атомной бомбы с тротиловым эквивалентом
 кг, если тепловой эквивалент тротила
q равен 4,19 МДж/кг.
кг, если тепловой эквивалент тротила
q равен 4,19 МДж/кг.При делении ядра урана под действием замедленного нейтрона образовались осколки с массовыми числами
 и
и
 .
Определить число нейтронов, вылетевших
из ядра в данном акте деления. Определить
энергию и скорость каждого из осколков,
если они разлетаются в противоположные
стороны и их суммарная кинетическая
энергия Т равна 160 МэВ.
.
Определить число нейтронов, вылетевших
из ядра в данном акте деления. Определить
энергию и скорость каждого из осколков,
если они разлетаются в противоположные
стороны и их суммарная кинетическая
энергия Т равна 160 МэВ.Ядерная реакция
 вызвана
-частицей,
обладавшей кинетической энергией
вызвана
-частицей,
обладавшей кинетической энергией
 МэВ. Определить тепловой эффект этой
реакции, если протон, вылетевший под
углом
= 60° к направлению движения -частицы,
получил кинетическую энергию
МэВ. Определить тепловой эффект этой
реакции, если протон, вылетевший под
углом
= 60° к направлению движения -частицы,
получил кинетическую энергию
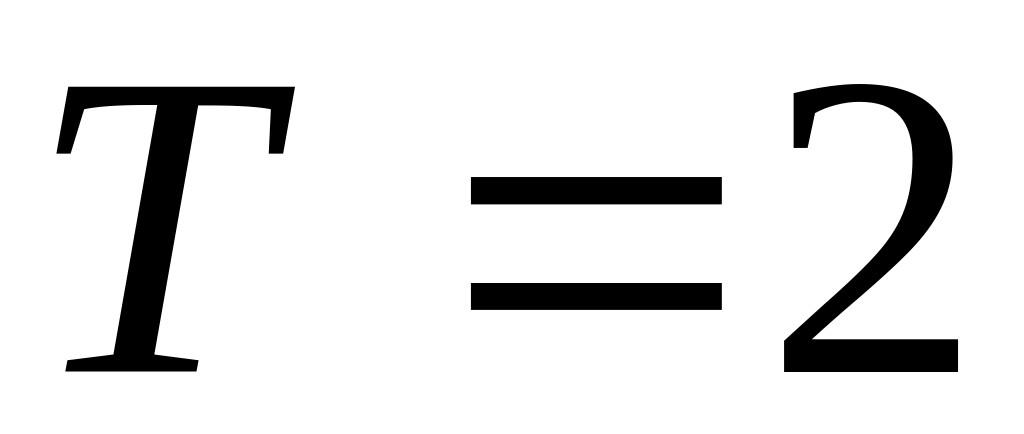 МэВ.
МэВ.Определить тепловые эффекты следующих реакций:
![]() и
и
![]()
Определить скорости продуктов реакции
 ,
протекающей в результате взаимодействия
тепловых нейтронов с покоящимися
ядрами бора.
,
протекающей в результате взаимодействия
тепловых нейтронов с покоящимися
ядрами бора.Ядро урана 235U при делении освобождает энергию 200 МэВ. При взрыве урановой бомбы успевает прореагировать около 1,5 кг урана. Какова масса эквивалентной тротиловой бомбы, если теплотворная способность тротила 4,1 МДж/кг?
Какую минимальную кинетическую энергию должна иметь -частица для осуществления ядерной реакции
 ?
?Найти минимальную кинетическую энергию протона, способного "разбить" ядро дейтерия на протон и нейтрон.
Атомная электростанция мощностью P = 1000 Вт имеет КПД 20%. Какова масса m расходуемого за сутки урана-235? Считать, что при каждом делении ядра урана выделяется энергия W0 = 200 МэВ.
Сколько железнодорожных вагонов массой M = 60 т каждый можно было бы поднять на высоту h = 1 км за счет энергии, вырабатываемой АЭС (см. предыдущую задачу) за сутки? На какую величину m уменьшается при этом масса ядерного горючего?
Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Возможен ли следующий процесс:
 ?
Объяснить.
?
Объяснить.Используя информацию о квантовых числах кварков, сконструировать из трех кварков следующие барионы: p, n, +. Ответ пояснить.
Используя информацию о квантовых числах кварков, сконструировать из кварка и антикварка следующие мезоны: +, –, K0. Ответ пояснить.
Мезон космических лучей имеет энергию W = 3 ГэВ. Энергия покоя мезона W0 = 100 МэВ. Какое расстояние l в атмосфере сможет пройти мезон за время его жизни по лабораторным часам? Собственное время жизни мезона 0 = 2 мкс.
Мезон космических лучей имеет кинетическую энергию W = 7m0c2, где m0 – масса покоя мезона. Во сколько раз собственное время жизни 0 мезона меньше времени его жизни по лабораторным часам?
Электрон и позитрон образуются фотоном с энергией 2,26 МэВ. Какова была в момент возникновения полная кинетическая энергия позитрона и фотона?
Неподвижный K0-мезон распадается на два заряженных -мезона. Масса покоя K0-мезона m0(K0)=965m0, где m0 – масса покоя электрона. Масса каждого -мезона m() = 1,77m0(), где m0() – его масса покоя. Найти массу покоя -мезонов.
Максимальный радиус кривизны траектории частиц в циклотроне R = 50 см, а магнитная индукция поля B = 1 Тл. Какую постоянную разность потенциалов должны пройти протоны, чтобы получить такое же ускорение, как в данном циклотроне?
В фазотроне увеличение массы частицы при возрастании ее скорости компенсируется увеличением периода ускоряющего поля. Частота разности потенциалов, подаваемой на дуанты фазотрона, менялась для каждого ускоряющего цикла от 0 = 25 МГ до = 18,9 МГ. Найти магнитную индукцию поля фазотрона и кинетическую энергию вылетающих протонов.
При упругом центральном столкновении нейтрона с неподвижным ядром замедляющего вещества кинетическая энергия нейтрона уменьшилась в 1,4 раза. Найти массу ядер замедляющего вещества.
Электрон ускорен разностью потенциалов U = 180 кВ. Учитывая поправки теории относительности, найти для этого электрона массу m.
До какой энергии E можно ускорить -частицы в циклотроне, если относительное увеличение массы частицы
 не должно превышать 5%?
не должно превышать 5%?Энергия дейтронов, ускоренных синхротроном, W = 200 МэВ. Найти скорость дейтронов. (масса покоя дейтрона m0 = 3,3510–27 кг)
Для получения медленных нейтронов их пропускают через вещества, содержащие водород, например, парафин. Какую наибольшую часть своей кинетической энергии нейтрон массой m0 может предать протону (масса m0).? Наибольшая часть передаваемой энергии соответствует упругому центральному столкновению.
Позитрон и электрон аннигилируют, образуя два фотона. Найти длину волны каждого из фотонов, считая, что начальная энергия частиц ничтожна мала.
Нейтрон и антинейтрон аннигилируют, образуя два фотона. Найти частоту каждого из фотонов, считая, что начальная энергия частиц ничтожно мала.
Заряженная частица влетает в однородное магнитное поле с индукцией B = 0,5 Тл и движется по окружности с радиусом R = 10 см. Скорость частицы v = 2,4106 м/с. Найти для этой частицы отношение ее заряда к массе.
Поток заряженных частиц влетает в однородное магнитное поле с индукцией B = 3 Тл. Скорость частиц v = 1,52107 м/с и направлена перпендикулярно к направлению поля. Найти заряд каждой частицы, если известно, что на нее действует сила F = 1,4610–11 Н.
Собственная угловая частота колебаний молекулы HCl равна 5,631014 с–1, коэффициент ангармоничности = 0,0201. Определить энергию E2,1 (в электрон-вольтах) перехода молекулы с первого на второй колебательный энергетический уровень.
См. условие задачи 8.1. Определить максимальное квантовое число max.
См. условие задачи 8.1. Определить максимальную колебательную энергию Emax (в электрон-вольтах).
См. условие задачи 8.1. Определить энергию диссоциации Ed (в электрон-вольтах).
Собственная круговая частота колебаний молекулы CO равна 4,081014 с–1,. Определить коэффициент квазиупругой силы.
Определить число колебательных энергетических уровней, которое имеет молекула HBr, если коэффициент ангармоничности = 0,0208.
Собственная круговая частота колебаний молекулы O2 равна 2,981014 с–1, коэффициент ангармоничности = 9,461–3. Определить максимальную колебательную энергию Emax (в электрон-вольтах) молекулы.
Для молекулы HF определить момент инерции. Межъядерное расстояние d = 91,7 пм.
Для молекулы HF определить вращательную постоянную B (в электрон-вольтах). Межъядерное расстояние d = 91,7 пм.
Для молекулы HF определить энергию (в электрон-вольтах), необходимую для возбуждения молекулы на первый вращательный уровень. Межъядерное расстояние d = 91,7 пм.
Определить момент импульса L молекулы кислорода, вращательная энергия которой равна 2,16 эВ.
Определить момент инерции J межъядерное расстояние d молекулы CO, если интервалы E между соседними линиями чисто вращательного спектра испускания молекулы CO равны 0,48 эВ.
Определить для молекулы HCl вращательные квантовые числа двух соседних уровней, разность энергий E+1, которых равна 7,86 эВ.
Для молекулы NO определить температуру T, при которой средняя кинетическая энергия поступательного движения молекулы равна энергии необходимой для ее возбуждения на первый вращательный энергетический уровень. Вращательная постоянная 0,212 эВ.
Найти момент L импульса двухатомной молекулы, соответствующий низшему энергетическому состоянию.
Определить теплоту Q, необходимую для нагревания кристалла калия массой m = 200 г от температуры T1 = 4 К до температуры T2 = 5 К. Принять характеристическую температуру Дебая для калия E = 100 К и считать условие
 о выполненным.
о выполненным.Вычислить характеристическую температуру
 Дебая для железа, если при температуре
Т = 20 К молярная
теплоемкость железа
Дебая для железа, если при температуре
Т = 20 К молярная
теплоемкость железа
 Дж/К·моль.
Условие
считать выполненным.
Дж/К·моль.
Условие
считать выполненным.Система, состоящая из N = 1020 трехмерных квантовых осцилляторов, находится при температуре
 (E = 250 К).
Определить энергию Е системы.
(E = 250 К).
Определить энергию Е системы.Медный образец массой m = 100 г находится при температуре T1 = 10 К. Определить теплоту Q, необходимую для нагревания образца до температуры T2 = 20 К. Можно принять характеристическую температуру для меди равной 300 К, а условие
 считать выполненным.
считать выполненным.Используя квантовую теорию теплоемкости Эйнштейна, определить коэффициент упругости связи атомов в кристалле алюминия. Принять для алюминия E = 300 К.
Найти отношение средней энергии
 линейного одномерного осциллятора,
вычисленной по квантовой теории, к
энергии
линейного одномерного осциллятора,
вычисленной по квантовой теории, к
энергии
 такого же осциллятора, вычисленной по
классической теории. Вычисление
произвести для двух температур: 1)
такого же осциллятора, вычисленной по
классической теории. Вычисление
произвести для двух температур: 1)
 ;
2)
,
где E
– характеристическая температура
Эйнштейна.
;
2)
,
где E
– характеристическая температура
Эйнштейна.Зная, что для алмаза E = 2000 К, вычислить его удельную теплоемкость при температуре Т = 30 К.
Молярная теплоемкость Cm серебра при температуре Т = 20 К оказалась равной 1,65 Дж/(моль·К). Вычислить по значению теплоемкости характеристическую температуру E. Условие считать выполненным.
Вычислить (по Дебаю) удельную теплоемкость хлористого натрия три температуре Т = E/20. Условие считать выполненным.
Вычислить по теории Дебая теплоемкость цинка массой m = 100 г при температуре T = 10 К. Принять для цинка характеристическую температуру Дебая E = 300 К и считать условие выполненным.
Определить частоту колебаний атомов серебра по теории теплоемкости Эйнштейна, если характеристическая температура серебра E = 165 К.
Определить среднюю энергию < > линейного, одномерного квантового осциллятора при температуре T = E = 200 К.
Определить теплоту Q, необходимую для нагревания кристалла меди массой m = 100 г от T1 = 10 К до T2 = 20 К. Характеристическая температура для меди E = 320 К. Считать условие выполненным.
Определить в электрон-вольтах максимальную энергию E фонона, который может возбуждаться в кристалле NaCl, характеризуемом температурой Дебая E = 320 К. Фотон какой длины волны обладал бы такой энергией?
Оценить расстояние между соседними атомами в кристалле меди, если скорость звука в меди v = 3550 м/с, а характеристическая температура для меди E = 320 К.
Пологая, что средняя энергия электрона равна 3/5 энергии Ферми, оценить давление электронного газа в кристалле алюминия. Энергия Ферми для алюминия EF = 12,8 эВ, концентрация электронов 21029 м–3.
Оценить долю электронов в меди, которые при ее нагревании до 100C выйдут за пределы уровня Ферми.
Определить какую температуру имел бы водород, средняя квадратичная скорость молекул которого равна максимальной скорости движения свободных электронов в кристалле лития при температуре абсолютного нуля. (Энергия Ферми для лития EF = 4,72 эВ)
Кусок серебра объемом V = 1 см3 находится при температуре T = 0 K. Определить массу электронного газа в металле, если энергия Ферми для серебра EF = 5,5 эВ.
Оценить температуру, при которой электронный газ в металле (медь) становится невырожденным. Энергия Ферми для меди EF = 7,1 эВ.
Определить температуру, при которой обычный невырожденный газ с массой молекул, равной массе электрона, имел бы энергию теплового движения, равную энергии Ферми некоторого металла, если концентрация электронного газа в этом металле n = 61028 м–3.
Вычислить для натрия и меди температуру вырождения электронного газа. (Энергия Ферми для меди 7,1 эВ, для натрия 3,1 эВ)
Определить энергию и импульс электрона на уровне Ферми для натрия и меди при температуре T = 0 K. Принять, что на каждый атом металла приходится по одному валентному электрону.
Определить среднюю квадратичную vкв скорость движения свободных электронов в металле (серебро) при T = 0 K. Принять, что на каждый атом металла приходится по одному валентному электрону.
Определить максимальную vF скорость движения свободных электронов в металле (литий) при T = 0 K. Принять, что на каждый атом металла приходится по одному валентному электрону.
Выразить среднюю квадратичную скорость vкв через максимальную скорость vF электронов в металле при T = 0 K.
Оценить температуру, при которой доля электронов в меди, вышедших за пределы уровня Ферми составляет 0,2%.
Определить долю свободных электронов в металле при температуре Т = 0 К, энергии E которых заключены в интервале значений от 0,5Emax до E max.
Металл находится при температуре T = 0 K. Определить во сколько раз число электронов с кинетической энергией от 0,5EF до EF больше числа электронов с энергией от 0 до 0,5EF.
Кусок меди объемом V = 20 см3 находится при температуре T = 0 K. Определить число N свободных электронов, энергии которых заключены в интервале значений от 0,5E max до Emax. Энергия Ферми EF = 7 эВ.
Германиевый кристалл, ширина запрещенной зоны в котором равна 0,72 эВ, нагревают от температуры t1 = 0°С до температуры t2 = 15°С. Во сколько раз возрастет его удельная проводимость?
При нагревании кремниевого кристалла от температуры t1 =0 до температуры t2 = 10°С его удельная проводимость возрастает в 2,28 раза. По приведенным данным определить ширину запрещенной зоны кристалла кремния.
p-n-переход находится под обратным напряжением U = 0,1 В. Его сопротивление R1 = 692 Ом. Каково сопротивление R2 перехода при прямом напряжении?
Металлы литий и цинк приводят в соприкосновение друг с другом при температуре Т = 0 К. На сколько изменится концентрация электронов проводимости в цинке? Какой из этих металлов будет иметь более высокий потенциал?
Сопротивление R1
 перехода,
находящегося под прямым напряжением
U = 1 В,
равно 10 Ом.
Определить сопротивление R2
перехода при обратном напряжении.
перехода,
находящегося под прямым напряжением
U = 1 В,
равно 10 Ом.
Определить сопротивление R2
перехода при обратном напряжении.Найти минимальную энергию
 ,
необходимую для образования пары
электрон-дырка в кристалле CaAs,
если его удельная проводимость
изменяется в 10 раз при изменении
температуры от 20 до 3°С.
,
необходимую для образования пары
электрон-дырка в кристалле CaAs,
если его удельная проводимость
изменяется в 10 раз при изменении
температуры от 20 до 3°С.Сопротивление R1 кристалла PbS при температуре t1 = 20 °С равно 104 Ом. Определить его сопротивление R2 при температуре t2 = 80 °С.
Каково значение энергии Ферми EF у электронов проводимости двухвалентной меди? Выразить энергию Ферми в джоулях и электрон-вольтах.
Прямое напряжение U, приложенное к переходу, равно 2 В. Во сколько раз возрастет сила тока через переход, если изменить температуру от T1 = 300 К до T2 = 273 К?
Электроды вакуумного фотоэлемента (один цезиевый, другой медный) замкнуты снаружи на коротко. Цезиевый электрод освещают монохроматическим электромагнитным излучением. Найти: 1) длину волны излучения, при которой появится фототок; 2) максимальную скорость фотоэлектронов, подлетающих к медному электроду, если длина волны излучения равна 220 нм.
Удельная проводимость кремния с примесями равна 112 См/м. Определить подвижность bp дырок и их концентрацию np, если постоянная Холла RH = 3,6610–4 м3/Кл. Принять, что полупроводник обладает только дырочной проводимостью.
Тонкая пластинка из кремния шириной l = 2 см помещена перпендикулярно линиям индукции однородного магнитного поля (B = 0,5 Тл). При плотности тока j = 2 мкА/мм2, направленного вдоль пластины, холловская разность потенциалов UH оказалась равной 2,8 В. Определить концентрацию n носителей заряда.
Собственный полупроводник (германий) имеет при некоторой температуре удельное сопротивление = 0,48 Омм. Определить концентрацию n носителей заряда, если подвижности bn и bp электронов и дырок соответственно равны 0,36 и 0,16 м2/(Вс).
Образец из германия n-типа в виде пластины длиной l = 10 см и шириной b = 6 мм помещена в однородное магнитное поле (B = 0,5 Тл) перпендикулярно линиям магнитной индукции. При напряжении U = 250 В, приложенном к концам пластины, возникает холловская разность потенциалов UH = 8,8 мВ. Определить постоянную Холла. Удельную проводимость германия приять равной 80 См/м.
Полупроводник в виде тонкой пластины шириной b = 1 см и длиной l = 10 см и помещен в однородное магнитное поле (B = 0,2 Тл) перпендикулярно линиям магнитной индукции. К концам пластины (по направлению l) приложено постоянное напряжение U = 300 В. Определить разность потенциалов UH на граях пластины, если постоянная Холла RH = 0,1 м3/Кл, удельное сопротивление = 0,5 См/м.
