Работа № 4

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА ПО МЕТОДУ КРУТИЛЬНЫХ КОЛЕБАНИЙ

Задание: определить модуль сдвига по методу крутильных колебаний с помощью кольца с предельной погрешностью , не превышающей 5%.

Принадлежности: проволока из исследуемого материала, диск, кольцо, секундомер, микрометр, линейка.

ЭЛЕМЕНТЫ ТЕОРИИ

Все без исключения тела под действием приложенных к ним внешних сил способны изменять свою форму и размеры, то есть деформироваться. Различают несколько видов деформаций: растяжение(сжатие), изгиб, сдвиг, кручение. Мы остановимся на рассмотрении деформаций сдвига и кручения.

СДВИГ

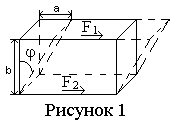Возьмём однородное тело, имеющее форму прямоугольного параллелепипеда , и приложим к его противоположным граням силы F₁ и F₂ (F₁ = F₂ = F), направленные параллельно этим граням (рисунок 1). Если действие сил равномерно распределено по всей поверхности соответствующей грани S, то в любом сечении параллельном этим граням, возникает тангенциальное напряжение

. (1)

Под действием напряжений тело деформируется таким образом, что верхняя грань сместится на некоторое расстояние a (рисунок 1). Если тело разбить на элементарные горизонтальные слои, то каждый слой окажется сдвинутым относительно соседних слоёв. По этой причине деформация такого вида получила название сдвига.

При деформации сдвига любая прямая, первоначально перпендикулярная горизонтальным слоям, повернётся на некоторый угол . В качестве характеристики деформации сдвига принимается отношение

. (2)

Величина  называется относительным сдвигом. Но в силу малости угла  можно положить tg = . Следовательно, относительный сдвиг  равен углу , называемому углом сдвига. Опыт показывает, что относительный сдвиг пропорционален тангенциальному напряжению(Закон Гука):

. (3)

Коэффициент G зависит только от свойств материала и называется модулем сдвига. Он равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 45^о, если бы при столь больших деформациях не был превзойдён предел упругости.

Рис. 2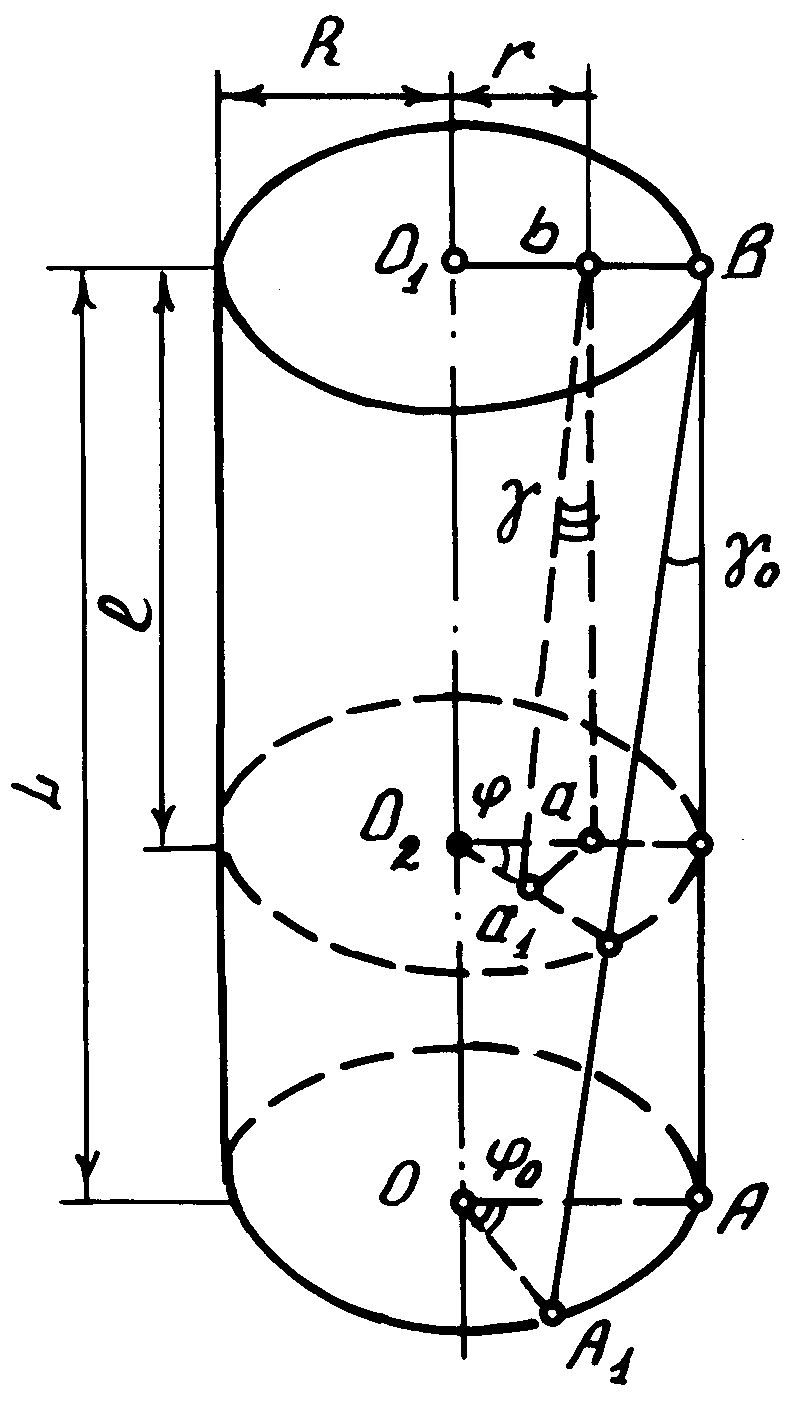

Деформация кручения. Пусть верхнее основание однородного стержня (например, проволоки) радиусом R и длиной L закреплено, а нижнее закручено вокруг оси O₁O на угол _o (рис. 2). Такая деформация называется кручением.

Мерой абсолютной деформации кручения является угол закручивания , который неодинаков в различных поперечных сечениях стержня (удаленных на разные расстояния  от верхнего основания). Величина / принимается за меру относительной деформации кручения. Для однородного стержня при малых деформациях она одинакова во всех сечениях.

При закручивании стержня его поперечные слои испытывают сдвиг относительно друг друга. Эта деформация неоднородна: в точках, расположенных на различных расстояниях r от оси O₁O, угол сдвига разный (см. рис. 2). На поверхности стержня этот угол максимальный и равен , на оси стержня он равен нулю.

Таким образом, деформацию кручения можно рассматривать как неоднородную деформацию сдвига. При малых деформациях угол сдвига

(4)

В соответствии с законом Гука тангенциальное напряжение

, (5)

где G – модуль сдвига. Отсюда

(6)

Следовательно, на разных расстояниях r от оси возникающие силы упругости, действующие на одинаковые площадки dS, различны.

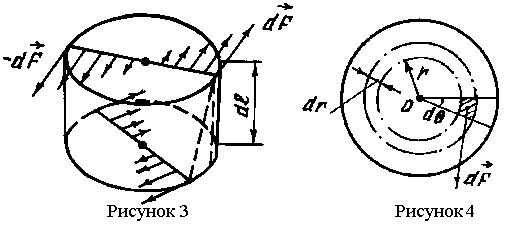
На верхнее и нижнее основания любого малого элемента стержня длиной dl (рис. 3) со стороны соседних частей стержня действуют силы упругости dF, определяемые соотношением (3). При равновесии модуль суммарного момента всех сил, действующих на верхнее основание, равен модулю момента сил, действующих на нижнее основание, т.е. модуль момента сил упругости в любом сечении однородного стержня одинаков. Рассчитаем его значение. Для этого в сечении стержня выделим площадку (заштрихована на рис. 4)

(7)

на которую действует сила упругости . Момент этой силы относительно оси стержня равен

(8)

Тогда с учетом (6) - (8)

. (9)

Для нижнего основания стержня момент сил

(10)

Коэффициент

, (11)

где d – диаметр проволоки, зависит не только от материала и физического его состояния, но и от геометрических размеров стержня. Для данного стержня эта величина постоянная и называется его модулем кручения.

Как следует из (10), толстые короткие стержни трудно подвергнуть закручиванию и, наоборот, длинные тонкие проволоки под воздействием даже очень малых моментов закручиваются на заметный угол. Этим пользуются при создании чувствительных подвесных систем в измерительных приборах.

Соотношение (10) выражает закон Гука для деформации кручения.

Крутильный маятник. Горизонтальный стержень, подвешенный на упругой проволочке, представляет собой крутильный маятник. Его колебания подчиняются основному уравнению динамики вращательного движения твердого тела:

(12)

где I – момент инерции маятника относительно оси вращения; – вектор углового ускорения маятника; – векторная сумма моментов (относительно той же оси) всех сил, действующих на маятник. Если силами сопротивления можно пренебречь, то из суммы останется только момент упругих сил, который при малых амплитудах колебаний определяется соотношением

(13)

где G – модуль сдвига материала проволоки, L – длина проволоки, R – её радиус, – вектор углового перемещения маятника ( – угол закручивания проволоки), D – модуль кручения. Соотношение (12) выражает закон Гука для деформации кручения. Знак “-” означает, что вектор момента упругих сил, возникающих в проволоке, направлен противоположно вектору углового перемещения .

Учитывая, что , уравнение (12) можно записать в виде

(14)

Уравнение (14) представляет собой уравнение гармонических колебаний переменной , квадрат циклической частоты которых равен коэффициенту перед . То есть, циклическая частота колебаний крутильного маятника равна

(15)

Период колебаний

(16)

Из (16) получаем

(17)

Теория метода. Экспериментальная установка состоит из длинн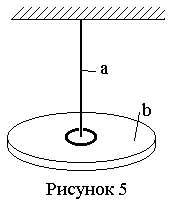 ой вертикально висящей проволоки а, к нижнему кольцу которой прикреплен диск b(рис 5).

На этот диск можно класть концентрическое кольцо, тем самым изменяя момент инерции I и период колебаний системы. Повернув диск на некоторый угол , отпускают его, вследствие чего диск начинает совершать колебания, период которых определяется по формуле (16). Подставив (11) в (16), получим

. (18)

Таким образом, для определения модуля сдвига G по методу крутильных колебаний с помощью кольца необходимо знать длину проволоки L, радиус её поперечного сечения R, момент инерции I и период колебаний системы Т. Для определения момента инерции системы I находим период колебаний системы без кольца , затем период колебаний с кольцом , где I₀ – момент инерции кольца.

, (19)

где m – масса, r₁ и r₂ – внутренний и внешний радиусы кольца.

. (20)

Выполнение работы

1. Измерить линейкой длину проволоки L.

2. Измерить внутренний и внешний радиусы кольца r₁ и r₂.

3. Повернув диск на некоторый угол, не превышающий 60⁰, с помощью секундомера измерить время пяти полных колебаний системы. Опыт повторить 3 раза. Найти среднее значение времени <t> и определить период крутильных колебаний по формуле T=<t>/5.

4. Аналогичные измерения и вычисления провести для системы с кольцом (период T₁).

5. Рассчитать момент инерции кольца I₀, момент инерции системы без кольца I, модуль сдвига материала проволоки G.

6. Результаты измерений и вычислений занести в таблицу :

№	m, кг	r1, м	r2, м	t, сек	T, сек	t1, сек	T1, сек	R, м	I0,кгм2	I,кгм2	G,н/м2
1
2
3

7. Оценить погрешности.

Контрольные вопросы

1. Деформация сдвига.

   1. На рисунке покажите векторы действующих сил.

   2. Какая величина характеризует относительную деформацию?

   3. Что такое напряжение?

   4. Закон Гука для деформации сдвига.

   5. Физический смысл модуля сдвига.

   6. От чего зависит модуль сдвига?

2. Деформация кручения.

   1. На рисунке покажите векторы под действием которых происходит деформация кручения в работе.

   2. Какие изменения происходят в проволоке при деформации кручения?

   3. Закон Гука для деформации кручения.

3. 1. Чему равен момент силы относительно точки?

   2. Направление и модуль вектора момента силы.

4. 1. Чему равен момент инерции точки, тела?

   2. Как изменяется момент инерции в работе при снятии кольца?

5. Вывести формулу, связывающую период крутильных колебаний с модулем кручения и моментом инерции.

Литература

1. Савельев И.В., Курс общей физики, том 1.

2. Трофимова Т.И., Курс физики.

3. Сивухин Д.В., Курс общей физики, том 1.

Приложение 1

Расчёт моментов инерции некоторых тел

Рис. 1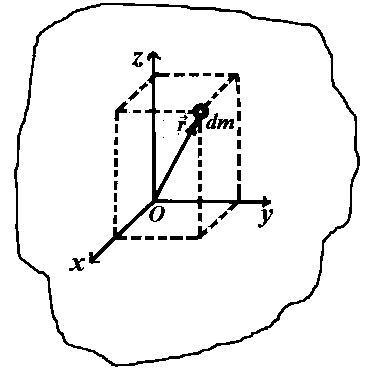

Момент инерции тела относительно оси и относительно точки. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси. Чтобы найти момент инерции тела (с непрерывным распределением вещества) относительно оси, надо мысленно разбить его на такие малые элементы, чтобы каждый из них можно было считать материальной точкой бесконечно малой массы dm = dV. Тогда момент инерции тела относительно оси равен интегралу по объёму тела:

(1)

где r – расстояние элемента dm до оси.

Вычисление момента инерции тела относительно оси часто упрощается, если предварительно вычислить его момент инерции относительно точки . Он вычисляется по формуле, аналогичной (1):

(2)

где r – расстояние элемента dm до выбранной точки (относительно которой вычисляется ). Пусть эта точка является началом системы координат X, Y, Z (рис. 1). Квадраты расстояний элемента dm до координатных осей X, Y, Z и до начала координат равны соответственно y²+z², z²+x², x²+y², x²+y²+z². Моменты инерции тела относительно осей X, Y, Z и относительно начала координат

Рис. 2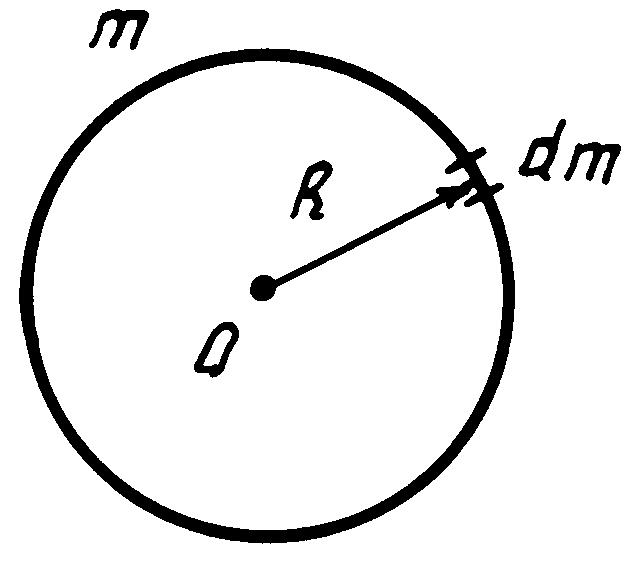

Из этих соотношений следует, что

(3)

Таким образом, сумма моментов инерции тела относительно трёх любых взаимно перпендикулярных осей , проходящих через одну точку, равна удвоенному моменту инерции тела относительно этой точки.

Момент инерции тонкого кольца. Все элементы кольца dm (рис. 2) находятся на одинаковом расстоянии, равном радиусу кольца R, от его оси симметрии (ось Y) и от его центра. Момент инерции кольца относительно оси Y

Рис. 3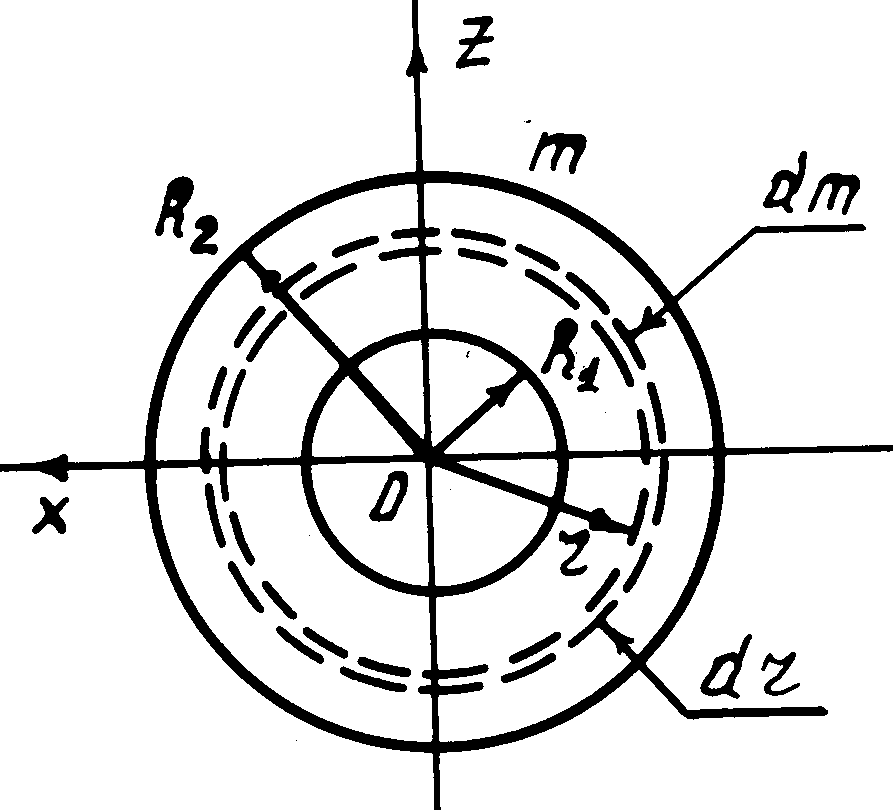

(4)

Момент инерции тонкого диска. Пусть тонкий однородный диск массы m с концентрическим отверстием (рис. 3) имеет внутренний и внешний радиусы R₁ и R₂. Мысленно разобьём диск на тонкие кольца радиуса r, толщины dr. Момент инерции такого кольца относительно оси Y (рис. 3, она перпендикулярна рисунку и не показана), в соответствии с (4)

(5)

Момент инерции диска

(6)

В частности, полагая в (6) R₁ = 0, R₂ = R, получим формулу для вычисления момента инерции тонкого сплошного однородного диска относительно его оси:

(7)

Момент инерции диска относительно его оси симметрии не зависит от толщины диска. Поэтому по формулам (6) и (7) можно вычислять моменты инерции соответствующих цилиндров относительно их осей симметрии.

Момент инерции тонкого диска относительно его центра также вычисляется по формуле (6),  = J_y, а моменты инерции относительно осей X и Z равны между собой, J_x = J_z. Поэтому, в соответствии с (3) 2J_x +J_y = 2J_y, J_x = J_y/2 или

(8)

Рис. 4

Момент инерции цилиндра. Пусть имеется полый симметричный цилиндр массы m, длины h, внутренний и внешний радиусы которого равны R₁ и R₂. Найдём его момент инерции относительно оси Z, проведенной через центр масс перпендикулярно оси цилиндра (рис. 4). Для этого мысленно разобьём его на диски бесконечно малой толщины dy. Один из таких дисков, массой dm = mdy/h, расположенный на расстоянии y от начала координат, показан на рис. 4. Его момент инерции относительно оси Z, в соответствии с (8) и теоремой Гюйгенса – Штейнера

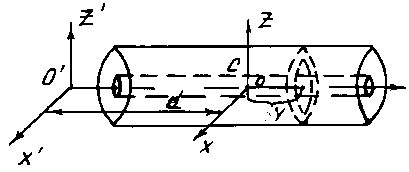
(9)

Момент инерции всего цилиндра

(10)

Момент инерции цилиндра относительно оси Z (оси вращения маятника) найдём по теореме Гюйгенса – Штейнера

где d – расстояние от центра масс цилиндра до оси Z. В работе 16 этот момент инерции обозначен как J_ц

(11)